2020.03,29日常总结

本文主要是介绍2020.03,29日常总结，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

$\color{green}{\text{洛谷P3627\ \ \ \ \ [APIO2009]抢掠计划}}$

$\color{blue}{\text{【题意】：}}$ Siruseri 城中的道路都是 $\color{red}{\text{单向}}$ 的。不同的道路由路口连接。按照法律的规定，在每个路口都设立了一个 Siruseri 银行的 ATM 取款机。令人奇怪的是，Siruseri 的酒吧也都设在路口，虽然并不是每个路口都设有酒吧。

Banditji 计划实施 Siruseri 有史以来最惊天动地的 ATM 抢劫。他将从市中心出发，沿着单向道路行驶，抢劫所有他途径的 ATM 机，最终他将在一个酒吧庆祝他的胜利。

使用高超的黑客技术，他获知了每个 ATM 机中可以掠取的现金数额。他希望你帮助他计算从市中心出发最后到达某个酒吧时最多能抢劫的现金总数。他可以经过同一路口或道路任意多次。但只要他抢劫过某个 ATM 机后，该 ATM 机里面就不会再有钱了。

例如，假设该城中有 $6$ 个路口，道路的连接情况如下图所示：
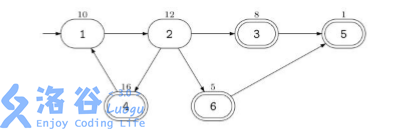
在这里插入图片描述
市中心在路口 $1$ ，由一个入口符号 $\to$ 来标识，那些有酒吧的路口用双圈来表示。每个 ATM 机中可取的钱数标在了路口的上方。在这个例子中，Banditji 能抢劫的现金总数为 $47$ ，实施的抢劫路线是： $\to 2 \to 4 \to 1 \to 2 \to 3 \to 5$ 。

$\color{blue}{\text{【思路】：}}$ 有向图的题目，很容易让人想到有向无环图（DAG）。因为 DAG 比有向有环图时的情况要简单得多。

所以，我们可以先用 tarjan 把原图缩点，顺便维护出每个 scc （强连通分量）中所有 ATM 内钱的总量 $\text{money}$ 和是否有酒店。

缩点后，原图变为了一个 DAG。我们可以用拓扑算法求解。代码如下：

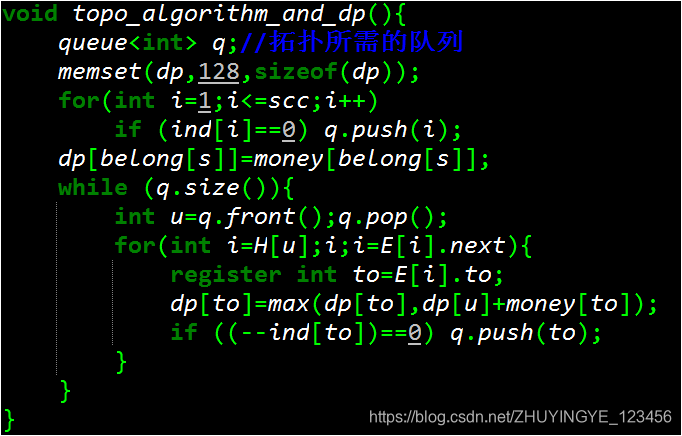
在这里插入图片描述
为什么这么做是可以的呢？因为 Banditji 可以重复走一条路很多次。我们进入一个 scc 后，因为 scc 内所有点可以直接或间接互相到达，所以我们一定要把它内的所有 ATM 全部抢完，否则不优。同时，因为 Banditji 可以重复走一条路很多很多次，所以抢完后，无论他在什么地方，他总能走到其它点从而到达其它 scc。

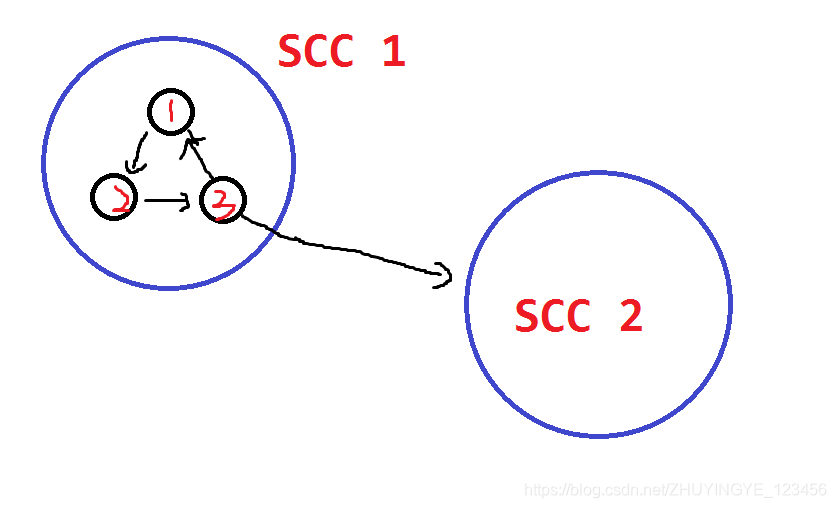
在这里插入图片描述
如图，蓝圈表示一个 scc，黑圈表示一个点。当 Banditji 在 SCC 1 中随意走到容易一个节点时，他都可以沿边走到 $3$ 号点，从而到达 SCC 2。所以，我们的算法是正确的。

下一个问题：如何求答案？很简单，求出所有有酒店的 SCC 中最大的 $\text{dp}$ 值即可。正因为它是一个 scc，所以 Banditji 无论在天涯海角，他都可以走到那个酒店中结束他的行程。正符合题意！！！

在这里插入图片描述
做到这里，这道题就算可以 AC 了。剩下的问题就是打 tarjan 算法的板子了。最后整理一下我们的思路：

1. tarjan 算法缩点——把有向有环图变成 DAG。
1. 建立一个只有 scc 的新图。
1. 调用拓扑排序算法辅以 $\text{dp}$ 求解（即 topo_algorithm_and_dp 函数）
1. 输出（即 print_the_answer 函数）

$\color{blue}{\text{【代码】：}}$

const int N=5e5+100;
struct edge{int next,to;
}e[N],E[N];int H[N],Tot,h[N],tot;
inline void add(int a,int b){e[++tot]=(edge){h[a],b};h[a]=tot;
}
inline void ADD(int a,int b){E[++Tot]=(edge){H[a],b};H[a]=Tot;
}
bool have_a_bar[N];
int n,m,s,p,value[N];
void read_the_data(){n=read();m=read();//专司输入 for(int i=1,u,v;i<=m;i++){u=read();v=read();add(u,v);}for(int i=1;i<=n;i++)value[i]=read();s=read();p=read();for(int i=1;i<=p;i++)have_a_bar[read()]=1;
}
int Stack[N],stack_top;
int dfn[N],low[N],dfscnt;
int belong[N],scc,num[N];
int money[N];bool bar[N];
void tarjan(int u){Stack[++stack_top]=u;low[u]=dfn[u]=++dfscnt;for(int i=h[u];i;i=e[i].next){register int to=e[i].to;if (dfn[to]==0){tarjan(to);//递归进行计算 low[u]=min(low[u],low[to]);}else if (belong[to]==0)low[u]=min(low[u],dfn[to]);}if (dfn[u]==low[u]){num[belong[u]=++scc]=1;bar[scc]=have_a_bar[u];money[belong[u]]=value[u];while (Stack[stack_top]!=u){int t=Stack[stack_top];num[belong[t]=scc]++;money[scc]+=value[t];bar[scc]|=have_a_bar[t];--stack_top;}--stack_top;}
}
int ind[N],dp[N],ans;
void build_new_picture(){for(int u=1;u<=n;u++)for(int i=h[u];i;i=e[i].next){register int to=e[i].to;if (belong[u]!=belong[to]){++ind[belong[to]];ADD(belong[u],belong[to]);}}
}
void topo_algorithm_and_dp(){queue<int> q;//拓扑所需的队列 memset(dp,128,sizeof(dp));for(int i=1;i<=scc;i++)if (ind[i]==0) q.push(i);dp[belong[s]]=money[belong[s]];while (q.size()){int u=q.front();q.pop();for(int i=H[u];i;i=E[i].next){register int to=E[i].to;dp[to]=max(dp[to],dp[u]+money[to]);if ((--ind[to])==0) q.push(to);}}
}
void print_the_answer(){for(int i=1;i<=scc;i++)if (bar[i]&&dp[i]>ans)ans=dp[i];printf("%d",ans);
}
int main(){read_the_data();for(int i=1;i<=n;i++)if (!dfn[i]) tarjan(i);build_new_picture();topo_algorithm_and_dp();print_the_answer();return 0;
}本代码已经 AC（本人亲自实验）且无任何反作弊系统。请读者放心。代码中的 read 函数就是快点函数（反正没人看，干脆不给了）