dog算子处理图片边界matlab代码,圖像邊緣檢測——二階微分算子（上）Laplace算子、LOG算子、DOG算子（Matlab實現）...

如果圖像灰度變化劇烈，進行一階微分則會形成一個局部的極值，由數學上的知識，對圖像進行二階微分則會形成一個過零點，並且在零點兩邊產生一個波峰和波谷，我們要設定一個閾值，檢測到這個過零點，如下圖所示：

帶來了兩個好處：

1. 二階微分關心的是圖像灰度的突變而不強調灰度緩慢變化的區域，對邊緣的定位能力更強。

2. Laplace算子是各項同性的，即具有旋轉不變性(后面會證明)，在一階微分里，我們是用|dx|+|dy|來近似一個點的梯度的，當圖像旋轉一個角度時，這個值就變化了，但對於Laplace算子來說不管圖像怎么旋轉，得到的響應是一樣的。

一個注意點：

我們檢測的必須是“過零點“，而不單單是零點，也就是要保證這個被選中的點一定要是局部極值點。比如下面這個例子，上面的曲線是圖像空間，虛線處的點並不是圖像的局部極值點，但求二階導的時候確實是零點。再比如圖像灰度的平坦區域，不管是一階導還是二階導都是0，它們顯然不是我們要的點：

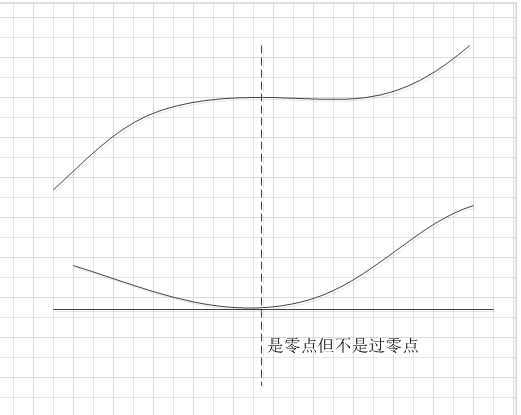
過零點的確定：

以p為中心的一個3*3領域，p點為過零點意味着至少有兩個相對的領域像素的符號不同。有四種要檢測的情況：左/右、上/下，和兩個對角。如果g(x,y)的值與一個閾值比較(一種通用的方法)，那么不僅要求相對領域的符號不同，數值差的絕對值要超過這個閾值，這時p稱為一個過零點像素。

Laplace算子

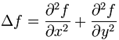
Laplace算子是梯度的散度 ：

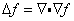
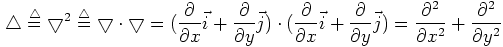
圖像是離散的二維矩陣，用差分近似微分：

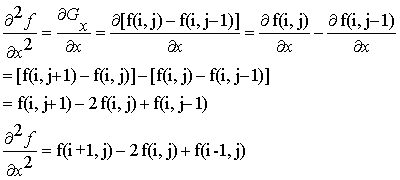
所以，

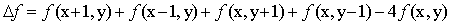
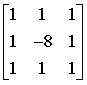
模板表示為：                                              其他常用的模板還有：

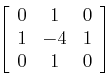
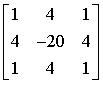
Laplace算子的旋轉不變性證明如下：

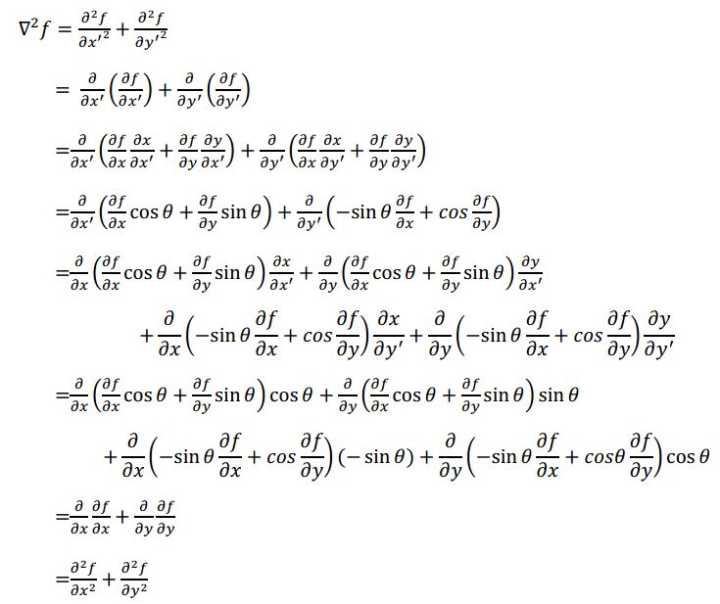
兩個缺點：

1.沒有了邊緣的方向信息；

2.雙倍加強了噪聲的影響。

在Matlab中的測試結果：

原圖：

原圖在不同閾值下的邊緣檢測效果：

加了椒鹽噪聲之后：

加了高斯噪聲之后：

代碼：

lenna = imread('E:\ImageTest\512\g512_006\lena.pgm');

%---------------------------------------------------------------------------

lenna_3=mat2gray(lenna); %圖像矩陣的歸一化

[m,n]=size(lenna_3);

lenna_4=lenna_3; %保留圖像的邊緣一個像素

L=0;

t=0.2; %設定閾值

%Laplace算子

for j=2:m-1

for k=2:n-1

L=abs(4*lenna_3(j,k)-lenna_3(j-1,k)-lenna_3(j+1,k)-lenna_3(j,k+1)-lenna_3(j,k-1));

if(L > t)

lenna_4(j,k)=255; %白

else

lenna_4(j,k)=0; %黑

end

end

end

figure;

imshow(lenna_4,[]);title('Laplacian 0.2')

可以明顯的看出，Laplace算子雖然解決了一階微分算子確定閾值的困難，但是卻不能克服噪聲的干擾。

於是LoG算子橫空出世。

LOG算子

1980年，Marr和Hildreth提出將Laplace算子與高斯低通濾波相結合，提出了LOG(Laplace and Guassian)算子。 步驟如下：

1.對圖像先進性高斯濾波(G

 × f)，再進行Laplace算子運算Δ(G

 × f)；

2.保留一階導數峰值的位置，從中尋找Laplace過零點；

3.對過零點的精確位置進行插值估計。

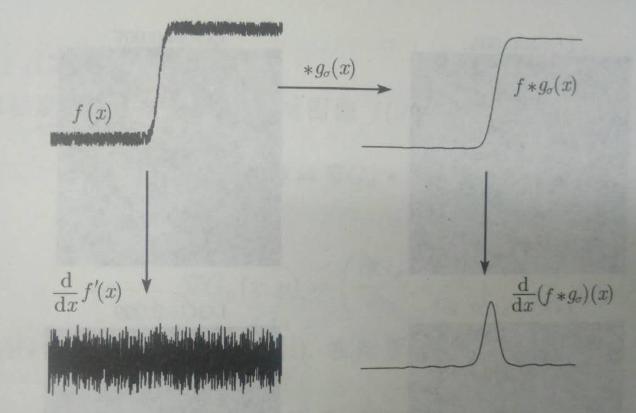
由上圖可以看出，高斯濾波之后邊緣信息才顯現出來。

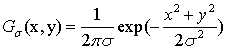
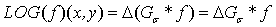  微分算子與卷積算子的次序可以交換。

LOG算子如下：

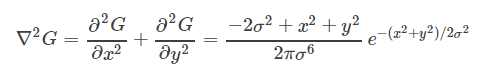
根據sigma的不同以及3sigma原則可以建立不同的模板，sigma是一個尺度參數，在圖像處理中引入尺度以及建立多尺度空間是一個重要的突破，sigma越大，圖像越模糊濾除噪聲效果越好，sigma越小，效果相反。

常用模板如下：

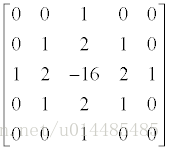
LOG的Matlab效果：

lenna = imread('E:\ImageTest\512\g512_006\lena.pgm');

subplot(121)

imshow(lenna,[]);title('原圖')

%-------------------------------------------------------------

%自帶函數

lenna=double(lenna);

lenna_1 = edge(lenna,'log');

subplot(122)

imshow(lenna_1,[]);title('LoG 0.5')

由數學上的關系，我們可以簡化LOG的計算——這便是DOG算子。

DOG算子

二維高斯對sigma求導：

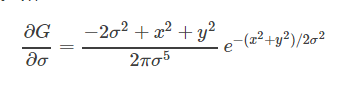
上面我們已經得到：

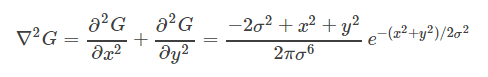
可以看出：

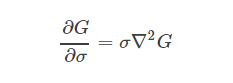
由導數定義：

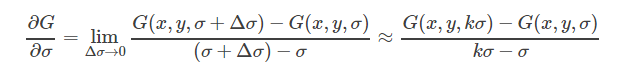
所以，

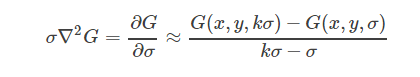
變形一下得到：

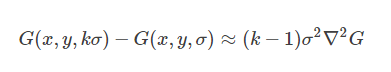
右邊比LOG算子只是多了一個系數，在實際應用中不影響。

我們定義：

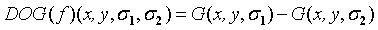
當我們用DOG算子代替LOG算子與圖像卷積的時候：

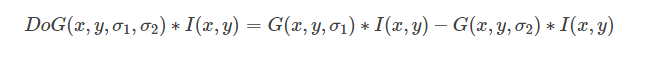
近似的LOG算子

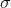值的選取：

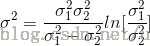
當使用這個值時，可以保證LoG和DoG的過零點相同，只是幅度大小不同。

這樣，我們只要對圖像進行兩次高斯平滑再將結果相減就可以近似得到LOG作用於圖像的效果了！

DOG的matlab效果：