本文主要是介绍深度之眼(十八)——偏导数与矩阵的求导,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、偏导数
- 二、多元复合函数的求导法则,链式求导法则
- 三、方向导数与梯度及其应用
- 四、多元函数泰勒公式与海森炬阵
- 五、多元角数的极值
- 六、距阵的求导
- 七、矩阵的求导在深度学习中的应用
一、偏导数


对某个变量求偏导,则其余变量看成常数


可以直接认为成立,不必拘泥条件
二、多元复合函数的求导法则,链式求导法则

这里举了一个不错的技巧,可以看z到t有几条路径
对多元时求偏导的方法
比如对x求偏导,就看到x的路径,有几条,分别经过什么



关键是画准链式关系
三、方向导数与梯度及其应用





举例


梯度的正方向,是梯度增长最快的方向。
梯度的负方向,是梯度减小最快的方向
四、多元函数泰勒公式与海森炬阵
一般用到二阶


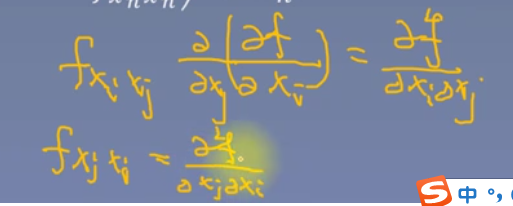
海森矩阵是个对称矩阵
五、多元角数的极值



六、距阵的求导


f(x)对其求偏导,就是个列向量,有几个变量,就有行
右值都是看成实数

解释之前的
J
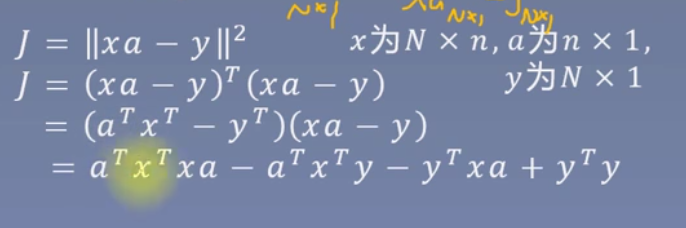
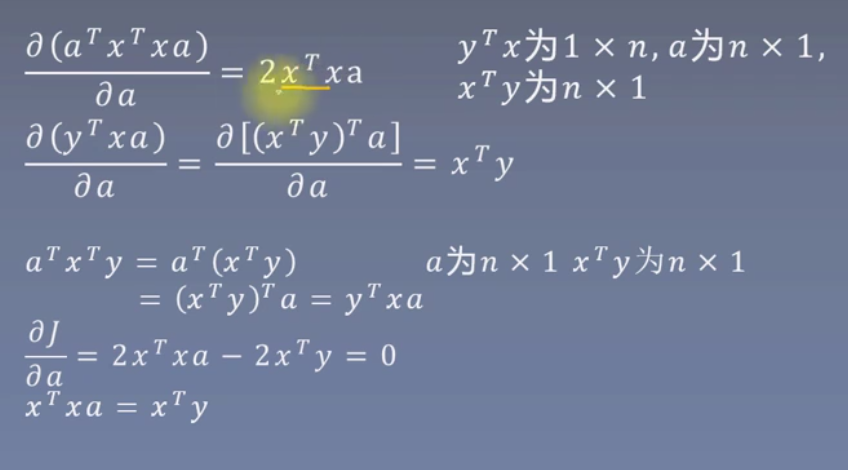
所以
J对a求偏导等于0,过程在上面



七、矩阵的求导在深度学习中的应用


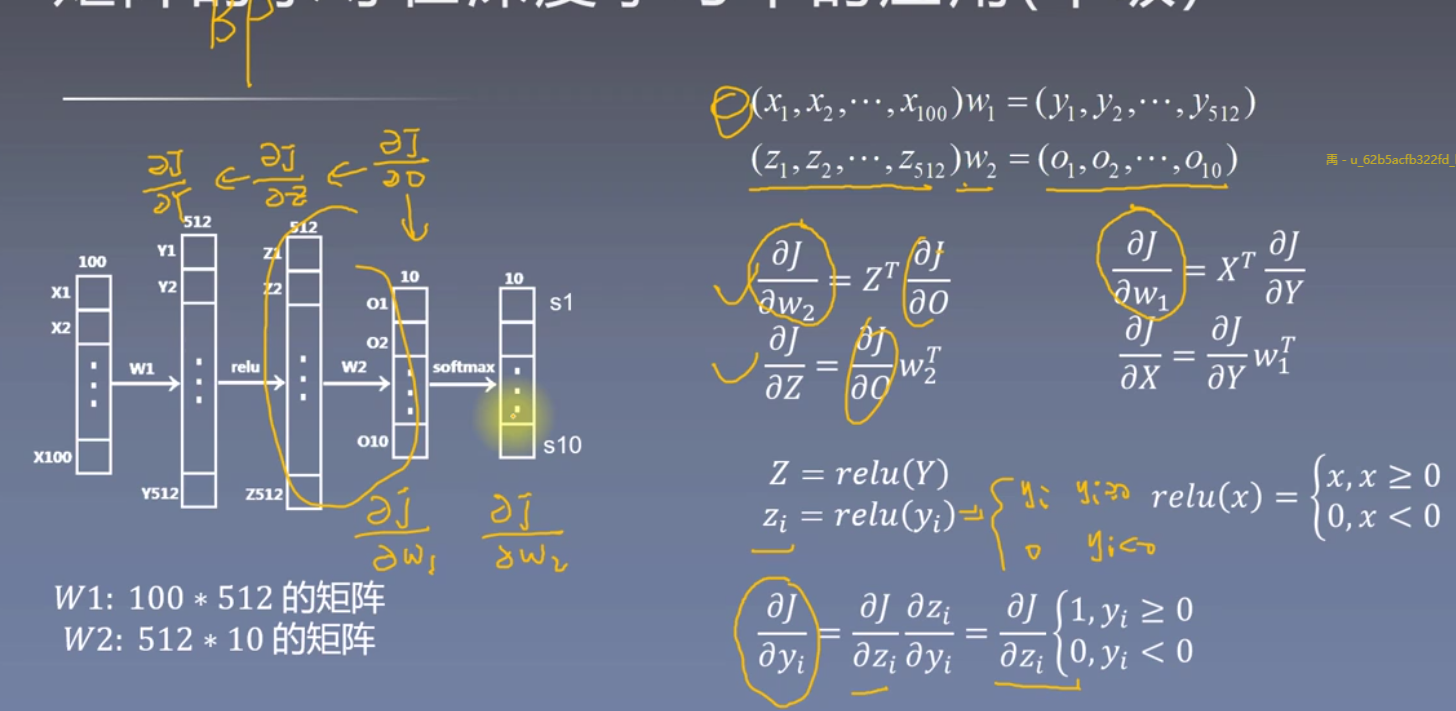
这篇关于深度之眼(十八)——偏导数与矩阵的求导的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





