SRM693-Biconnected

分析：
首先，如果你认为是图论或者其他算法，我并不认为做不出来。但至少DP是能做的。

因为虽然题目各方面都是与图有关，但其实仔细想想，这个图已经被固定了，唯一有变化的就是边权。不难想到很多DP模型都是这个样子，满足统一的特征或者结构，但具体的数值有所不同。最重要的是，这个图很明显是一个近似于一条链的东西。
由此，我们猜想可以用DP来做。

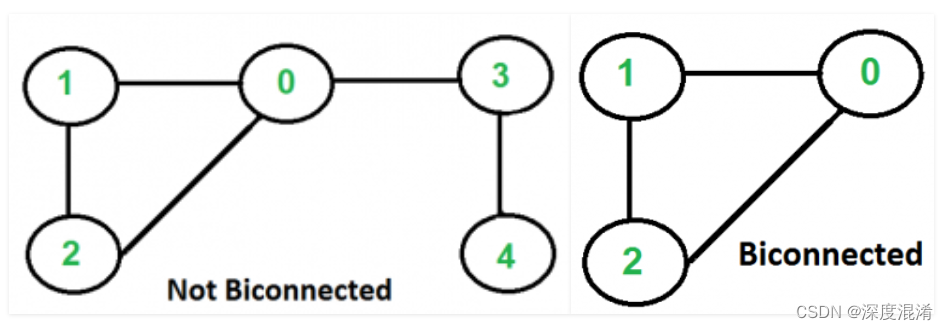
最开始必须明确一个基本性质：任何一个点的度数都必须大于1（否则就会被孤立，就没有双连通图的性质了）

为了方便起见（更多是因为经验所得），我们只考虑每个点向前连接的边的删除情况。
那么总共有4种情况：
①全部删除：是不可能的。
这样做相当于将图变为两个图

那么红线上的边就会成为左右两图的必经之路，不合法。
②全部不删除：那么对图的合法性没有任何危害，从任何一个合法状态转移都没问题。
③只删长边：
那么就只能从前一个点不删边的状态转移过来。因为当前如果删去长边，就会使前一个点为分割线，将原图拆成两个图（和①有些类似）

这时前一个点就成了前一个图的末尾点，是不能删边的。
④只删短边：
那么就可以从前一个点任何一种情况转移过来：
如果前一个点是删去的短边，那么继续向前考虑
如果前一个点保留了短边（删去长边或者都没删），那么就会从这个短边开始，形成一个环。

因为这个图第一个点向后连的边一定不能删，所以环路的左端点有保证
因为这个图最后一个点向前连的边一定不能删，所以环路的右端点有保证。

这样DP就没问题了

#include<cstdio>
#include<cstring>
#include<algorithm>
#define SF scanf
#define PF printf
#define MAXN 110
using namespace std;
int n,a[MAXN],b[MAXN],tot;
int dp[MAXN][2][2];
int main(){SF("%d",&n);for(int i=1;i<=n;i++){SF("%d",&a[i]);tot+=a[i];  }for(int i=1;i<n;i++){SF("%d",&b[i]);tot+=b[i];  }for(int i=3;i<=n+1;i++){dp[i][1][0]=max(dp[i-1][1][1],max(dp[i-1][0][1],dp[i-1][1][0]))+a[i-1];if(i>3)dp[i][0][1]=dp[i-1][1][1]+b[i-2];dp[i+1][1][1]=max(dp[i][1][1],max(dp[i][1][0],dp[i][0][1]));}PF("%d",tot-dp[n+1][1][1]);
}