一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等

本文主要是介绍一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

正态分布

对数正态分布

伽马分布

伽马函数

贝塔函数

伽马分布

卡方分布

F分布

t分布

附录

参考文献

本文主要介绍一些常见的分布，包括正态分布、对数正态分布、伽马分布、卡方分布、F分布、t分布。给出了分布的定义，推导了概率密度函数，以及函数图像。

正态分布

当 $n=0,\sigma^2=1$ ，称为标准正态分布，即 $X\sim N(0,1)$ 。

对数正态分布

对数正态分布（logarithmic normal distribution）是指一个随机变量的对数服从正态分布，则该随机变量服从对数正态分布。对数正态分布从短期来看，与正态分布非常接近。但长期来看，对数正态分布向上分布的数值更多一些。

证明：

假设 $Y$ 服从的正态分布为 $G(x)$ ，概率密度函数为 $g(x)$ ， $X$ 服从的分布为 $F(x)$ ，概率密度函数为 $f(x)$ 。显然有 $G^{'}(x)=g(x),F^{'}(x)=f(x)$ 。

下面证明 $X$ 的概率密度函数 $f(x)$ 表达式如上面所示。

一般我们通过分布函数和概率的定义来证明。

$F(x)=P(X\leq x)$ ，因为 $Y=lnX$ ，则 $X=e^Y$ ,

$P(X\leq x)=P(e^Y\leq x)=P(Y\leq lnx)=G(lnx)$

即

$F(x)=G(lnx)$ ，两边对 $x$ 求导，得到：

$\frac{\mathrm{dF(x)} }{\mathrm{d} x}=\frac{\mathrm{dG(lnx)} }{\mathrm{d} x}$ ，即：

$f(x)=\frac{g(lnx)}{x}$ ，注意到正态分布概率密度函数 $g(x)$ 如下：

$g(x)$

代入后，可得到 $f(x)$ 表达式如上面所示。

伽马分布

伽马函数

在介绍伽马分布之前，我们先对伽马函数有一个基本理解，伽马函数如下：

$\alpha$ 是自变量。伽马函数图像如下：

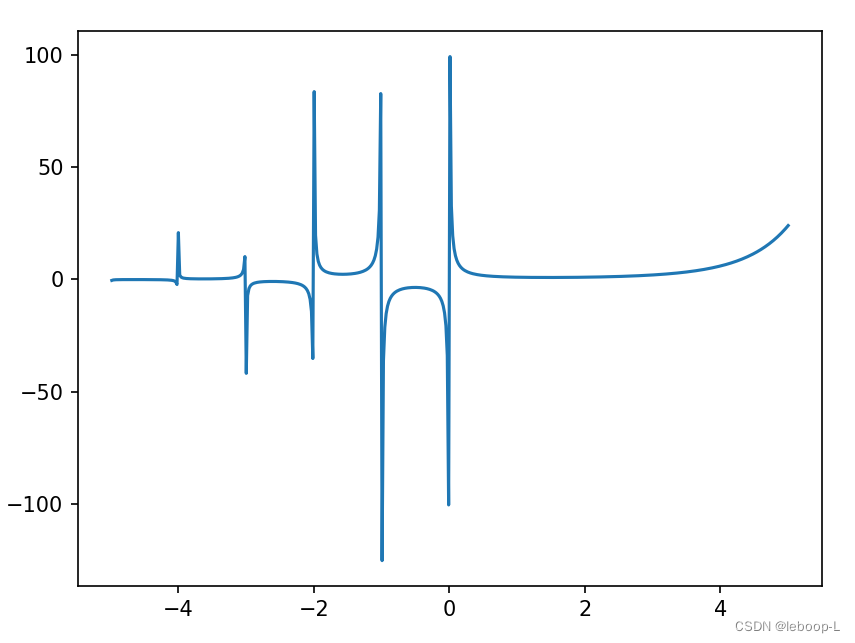
伽马函数图像绘制代码，如下：

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gammaif __name__ == '__main__':x = np.linspace(-5, 5, 500) # -5到5之间生成500个点y = gamma(x)    # 计算y的值，也就是伽马函数的值plt.plot(x, y)plt.show()

为了后面方便推导卡方分布，这里我们证明 $\Gamma(\frac{1}{2})=\sqrt{\pi}$ 。

下面利用标准正态分布的概率密度函数曲线下的面积为1来证明。即：

$\int_{-\infty }^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx=1$

由正态分布对称性，得到

$2\int_{0 }^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx=1$

令 $t=\frac{x^2}{2}$ 进行换元，

$2\int_{0 }^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-t}d\sqrt{2t}=1$

$2\int_{0 }^{+\infty}\frac{1}{\sqrt{2\pi}}e^{-t}\frac{1}{\sqrt{2t}}dt=1$

$\int_{0 }^{+\infty}\frac{1}{\sqrt{\pi t}}e^{-t}dt=1$

$\int_{0 }^{+\infty}\frac{1}{\sqrt{t}}e^{-t}dt=\sqrt{\pi}$

因为伽马函数如下：

知道

$\Gamma(\frac{1}{2})=\int_{0 }^{+\infty}\frac{1}{\sqrt{t}}e^{-t}dt=\sqrt{\pi}$

伽马函数还有其他很多的函数表达式，这里不再累述。

贝塔函数

在概率统计和其他应用学科中会经常用到伽玛函数和贝塔函数，有的反常积分的计算最后也会归结为贝塔函数或伽玛函数。贝塔函数又称为第一类欧拉积分，而第二类欧拉积分就是大名鼎鼎的伽玛函数Γ(x。贝塔函数具有很好的性质，以及实用的递推公式，另外需要注意的是伽玛函数和贝塔函数之间的关系。贝塔函数如下：

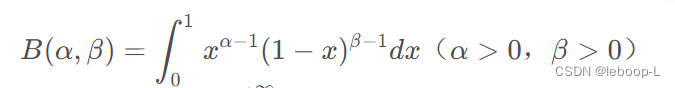
贝塔函数是一个积分形式， $\alpha,\beta$ 为参数。

下面推导伽马函数与贝塔函数之间存在的关系。我们先给出他们的关系：

$B(\alpha, \beta )=\frac{\Gamma(\alpha)\Gamma(\beta )}{\Gamma(\alpha +\beta )}$

由伽马函数：

得到

$\Gamma(\alpha )\Gamma(\beta )=\int_{0}^{+\infty}t^{\alpha-1}e^{-t}dt\times\int_{0}^{+\infty}s^{\beta-1}e^{-s}ds$

$=\int_{0}^{+\infty}\int_{0}^{+\infty}t^{\alpha-1}s^{\beta-1}e^{-(t+s)}dtds$

使用如下积分换元 $t=uv,s=u(1-v)$ ，即

$u=s+t,v=\frac{t}{s+t}$

容易得到 $u\in(0,+\infty),v\in(0,1)$ ，并且s=0时，v=1, $s \to +\infty$ 时，v=0。变换前后微元关系如下：

$dtds=\begin{vmatrix} \frac{\partial t}{\partial u} & \frac{\partial t}{\partial v} \\ \frac{\partial s}{\partial u} & \frac{\partial s}{\partial v} \end{vmatrix}dudv=\begin{vmatrix} v & u\\ 1-v & -u \end{vmatrix}dudv$

$=[-uv-u(1-v)]dudv=-ududv$

则换元后，原式如下：

$\Gamma(\alpha )\Gamma(\beta )=$

$=\int_{0}^{+\infty}\int_{1}^{0}(uv)^{\alpha-1}[u(1-v)]^{\beta-1}e^{-u}(-u)dudv$

$=\int_{0}^{+\infty}\int_{0}^{1}(uv)^{\alpha-1}[u(1-v)]^{\beta-1}e^{-u}(u)dudv$

$=\int_{0}^{+\infty}u^{\alpha+\beta-1}e^{-u}du\times\int_{0}^{1}v^{\alpha-1}(1-v)^{\beta-1}dv$

$=\Gamma(\alpha+\beta)B(\alpha,\beta)$

即：

$B(\alpha, \beta )=\frac{\Gamma(\alpha)\Gamma(\beta )}{\Gamma(\alpha +\beta )}$

为了直观地理解贝塔函数，下面我们绘制出贝塔函数的三维曲面图像。代码如下：

import numpy as np
from scipy.special import beta
import matplotlib.pyplot as pltif __name__ == '__main__':# 创建一个网格x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))print('x=', '\n', x)print('y=', '\n', y)z = beta(x, y)print('z=', '\n', z)plt.rcParams['font.sans-serif'] = ['Simhei']  # 显示中文fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')ax.tick_params(axis="both", labelsize=12)ax.plot_surface(x, y, z, cmap='viridis')ax.set_xlabel('x', fontsize=13)ax.set_ylabel('y', fontsize=13)ax.set_zlabel('z')ax.set_title('贝塔函数图像')plt.show()

运行结果，如下：

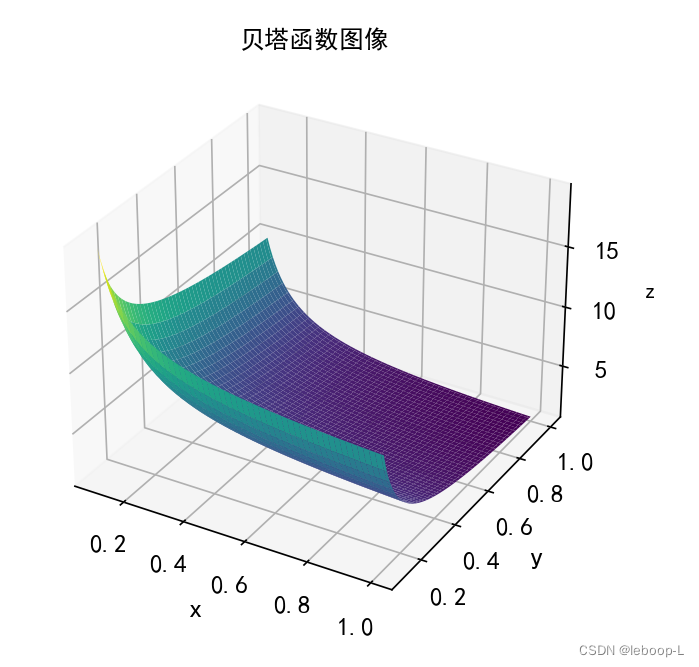
伽马分布

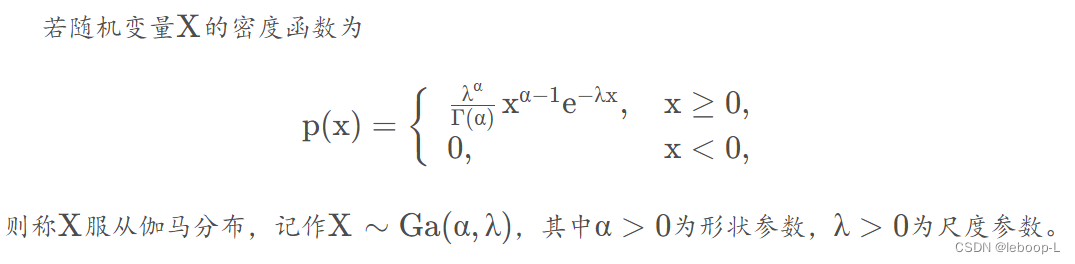
从定义可以看到，伽马分布的概率密度函数的分母中 $\Gamma(\alpha )$ 就是伽马函数。可以通过scipy提供的统计库stats，绘制出正态分布、对数正态分布、伽马分布的概率密度函数曲线，代码如下：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma as gamma_dis
from scipy.stats import lognorm
from scipy.stats import normif __name__ == '__main__':alpha = 2  # 伽马分布的形状参数theta = 2  # 伽马分布的比例参数# 创建一个 sample spacex = np.linspace(0, 10, 200)# 计算概率密度函数 (PDF)gamma_pdf = gamma_dis.pdf(x, alpha, scale=theta)  # 伽马分布概率密度函数log_norm_pdf = lognorm.pdf(x, loc=0, s=1)  # 对数正态分布概率密度函数norm_pdf = norm.pdf(x, loc=0, scale=1)  # 正态分布概率密度函数plt.rcParams['font.sans-serif'] = ['Simhei']  # 显示中文# 绘制伽马分布曲线plt.plot(x, gamma_pdf)plt.plot(x, log_norm_pdf)plt.plot(x, norm_pdf)plt.legend(['伽马分布', '对数正态分布', '正态分布'])  # 设置图例plt.title('概率密度函数曲线')plt.xlabel('x')plt.ylabel('概率密度函数值')plt.show()

运行结果如下：

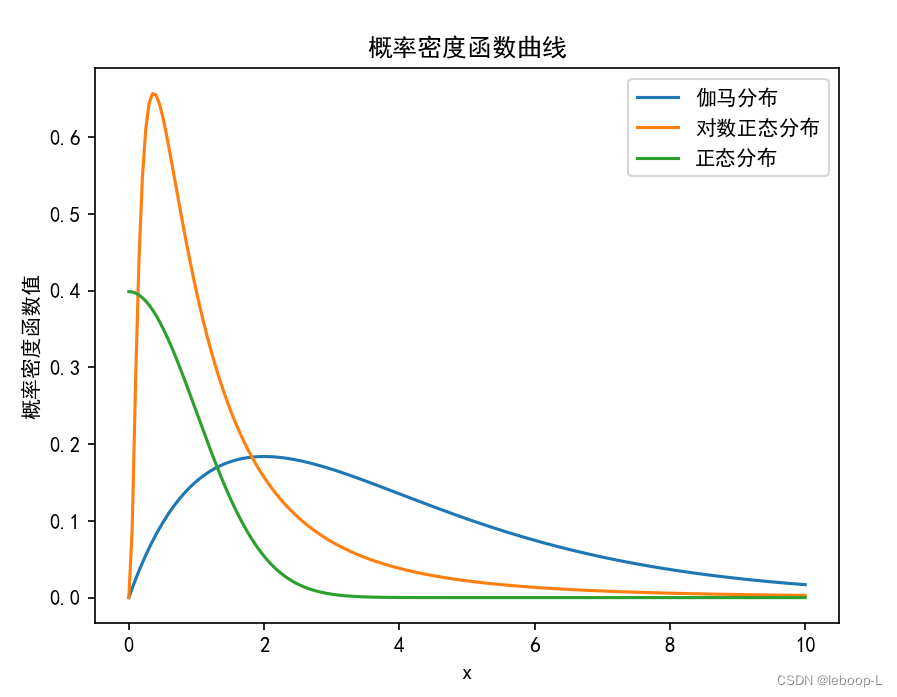
伽马分布有如下重要的性质：

（1）设随机变量 $X\sim Ga(\alpha_1,\lambda )$ ， $Y\sim Ga(\alpha_2,\lambda )$ ，且 $X,Y$ 相互独立，则 $Z=X+Y\sim Ga(\alpha_1+\alpha_2,\lambda )$ 。

证明：

假设随机变量 $Z$ 的分布为 $F(z)$ ，概率密度函数为 $f_Z(z)$ ，随机变量 $X,Y$ 的概率密度函数分别为 $f_X(x)$ ， $f_Y(x)$ 。两者的联合概率密度函数为 $f_{XY}(x,y)$ ，因为 $X,Y$ 相互独立，显然有：

$f_{XY}(x,y)=f_X(x)f_Y(x)$

因为

$X,Y$ 取值都在 $(0,+\infty)$ ，所以 $Z$ 的取值也在 $(0,+\infty)$ ，从而当 $z\leq 0$ 时， $f_Z(z)=0$ 。

当 $z> 0$ 时， $F(z)=P(Z\leq z)=P(X+Y\leq z)$ ，这里将z看成常数，有

$F(z)=\iint_{x+y\leq z}f_{XY}(x,y)dxdy$

$=\iint_{x+y\leq z}f_X(x)f_Y(y)dxdy$

$=\int_{-\infty}^{+\infty}f_X(x)dx\int_{-\infty}^{z-x}f_Y(y)dy$

使用换元 $t=x+y$ ，将x看陈常数，有

$y\in(-\infty,z-x)$ ，则 $t\in(-\infty,z)$ ，且 $dy=dt$ ，

得到

$F(z)=\int_{-\infty}^{+\infty}f_X(x)dx\int_{-\infty}^{z}f_Y(t-x)dt$

$F(z)=\int_{-\infty}^{z}[\int_{-\infty}^{+\infty}f_X(x)f_Y(t-x)dx]dt$

两边对z求导，得到

$f_Z(z)=\int_{-\infty}^{+\infty}f_X(x)f_Y(z-x)dx$ 。

这就是卷积公式。因为

$X\sim Ga(\alpha_1,\lambda )$ ， $Y\sim Ga(\alpha_2,\lambda )$ ，代入得到

$f_Z(z)=\int_{0}^{z}\frac{\lambda^{\alpha_1}}{\Gamma(\alpha_1)}x^{\alpha_1-1}e^{-\lambda x}\frac{\lambda^{\alpha_2}}{\Gamma(\alpha_2)}(z-x)^{\alpha_2-1}e^{-\lambda (z-x)}dx$

$f_Z(z)=\frac{\lambda^{\alpha_1+\alpha_2}e^{-\lambda z}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}\int_{0}^{z}x^{\alpha_1-1}(z-x)^{\alpha_2-1}dx$

使用换元 $x=zt$ ，当 $x\in(0,z)$ 时， $t\in(0,1)$ ，并且 $dx=zdt$ ，则

$f_Z(z)=\frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}e^{-\lambda z}\int_{0}^{1}(zt)^{\alpha_1-1}(z-zt)^{\alpha_2-1}zdt$

$=\frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}z^{\alpha_1+\alpha_2-1}e^{-\lambda z}\int_{0}^{1}t^{\alpha_1-1}(1-t)^{\alpha_2-1}dt$

$=\frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)}z^{\alpha_1+\alpha_2-1}e^{-\lambda z}B(\alpha_1,\alpha_2)$

根据 $B(\alpha, \beta )=\frac{\Gamma(\alpha)\Gamma(\beta )}{\Gamma(\alpha +\beta )}$ ，得到

$f_Z(z)=\frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1+\alpha_2)}z^{\alpha_1+\alpha_2-1}e^{-\lambda z}$ ，所以

$Z=X+Y\sim Ga(\alpha_1+\alpha_2,\lambda )$

卡方分布

假设n个相互独立的随机变量 $X_1,X_2,...,X_n$ ，均服从标准正态分布（也称独立同分布于标准正态分布） $N(0,1)$ 。则这n个服从标准正态分布的随机变量的平方和 $Q=\sum_{i=1}^nX_i^2$ 构成一个新的随机变量，其分布规律称为卡方分布（chi-square distribution），记作 $Q\sim \chi^2(n)$ ，n称为卡方分布的自由度（degree of freedom），记作 $df=n$ 。

这个分布由麦克斯韦(James Clerk Maxwell, 1831-1879)在研究空气分子的运动速度的分布时发现的，他发现分子运动速度 $v$ 的平方服从自由度为3的卡方分布，即 $v^2\sim \chi^2(3)$ 。后来又有多人提出这种分布，例如弗里德里希·罗伯特·海尔默特(Friedrich Robert Helmert, 1843-1917)于1875年，故卡方分布有时（在德国常见，因海尔默特是德国人）也称海尔默特分布；另外，这一结果被英国生物统计学家、优生学家、数理统计学创始人和社会达尔文主义理论家卡尔·皮尔逊(Karl Pearson, 1857-1936)推广并于1900年发表。

卡方分布 $\chi^2(n)$ 的概率密度函数

$f(x,n)=\frac{x^{\frac{n}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}$

下面来推导。

（1）当df=1时， $Q=X_1^2$ 。卡方分布的概率密度函数变为：

$f(x,1)=\frac{e^{-\frac{x}{2}}}{\sqrt{2x} \Gamma(\frac{1}{2})}=\frac{1}{\sqrt{2\pi x}}e^{-\frac{x}{2}}$

假设随机变量 $Q$ 的分布函数为 $F(x)$ ，概率密度函数为 $f(x)$ ，随机变量 $X_1$ 的分布函数为 $F_{X_1}(x)$ ，概率密度函数为 $f_{X_1}(x)$ ，随机变量 $X_2$ 的分布函数为 $F_{X_2}(x)$ ，概率密度函数为 $f_{X_2}(x)$ 。因为 $X_1$ ， $X_2$ 服从标准正态分布，有

$f_{X_1}(x)=f_{X_2}(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$ 。

因为 $F(x)=P(Q<x)=P(X_1^2<x)=P(-\sqrt{x}<X_1<\sqrt{x})$

$=P(X_1<\sqrt{x})-P(X_1<-\sqrt{x})=F_{X_1}(\sqrt{x})-F_{X_2}(-\sqrt{x})$

两边对x求导，

$f(x)=\frac{1}{2\sqrt{x}}(f_{X_1}(\sqrt{x})+f_{X_2}(-\sqrt{x}))$

因为 $f_{X_1}(x)=f_{X_2}(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$ ，所以：

$f(x)=\frac{1}{2\sqrt{x}}(\frac{1}{\sqrt{2\pi}}e^{-\frac{x}{2}}+\frac{1}{\sqrt{2\pi}}e^{-\frac{x}{2}})$

即

$f(x)=\frac{1}{\sqrt{2\pi x}}e^{-\frac{x}{2}}$

事实上，它是 $\alpha=\frac{1}{2},\lambda=\frac{1}{2}$ 的伽马分布，即 $Q\sim Ga(\frac{1}{2},\frac{1}{2})$ 。根据如下伽马分布的概率密度函数，很容易得出。

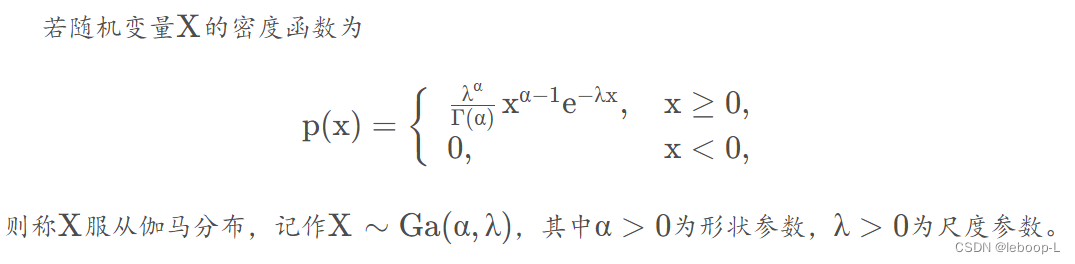
（2）当df=n时， $Q=\sum_{i=1}^nX_i^2$ ，由上面的结论知道， $X_i^2\sim Ga(\frac{1}{2},\frac{1}{2})$ 。另外因为 $X_1,X_2,...,X_n$ 相互独立，所以 $X_1^2,...,X_i^2,...,X_n^2$ 也相互独立。根据之前证明的如下结论：

如果随机变量 $X\sim Ga(\alpha_1,\lambda )$ ， $Y\sim Ga(\alpha_2,\lambda )$ ，且 $X,Y$ 相互独立，则 $Z=X+Y\sim Ga(\alpha_1+\alpha_2,\lambda )$ 。

得到 $Q=\sum_{i=1}^nX_i^2$ 服从 $Ga(\frac{n}{2},\frac{1}{2})$ ，代入伽马分布，得到如下卡方分布

$f(x,n)=\frac{x^{\frac{n}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}$

从结论来看，卡方分布是伽马分布的一个特例，即 $Ga(\frac{n}{2},\frac{1}{2})$ 。也就是说

$\chi^2(n)=Ga(\frac{n}{2},\frac{1}{2})$ 。

为了直观的观测卡方分布，下面使用python代码绘制卡方分布曲线。代码如下：

import numpy as np
from scipy.special import beta
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# # 创建一个网格# x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))# print('x=', '\n', x)# print('y=', '\n', y)# z = beta(x, y)# print('z=', '\n', z)#plt.rcParams['font.sans-serif'] = ['Simhei']  # 显示中文# fig = plt.figure(figsize=(10, 8))# ax = fig.add_subplot(111, projection='3d')# ax.tick_params(axis="both", labelsize=12)# ax.plot_surface(x, y, z, cmap='viridis')# ax.set_xlabel('x', fontsize=13)# ax.set_ylabel('y', fontsize=13)# ax.set_zlabel('z')# ax.set_title('贝塔函数图像')# plt.show()X = np.linspace(0.1, 14, 500)plt.subplots(figsize=(8, 5))plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=4), label="4 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=6), label="6 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=11), label="11 d.o.f")plt.title("卡方分布")plt.legend()plt.show()

代码中绘制了自由度为1，2，3，4，11的5个卡方分布，运行结果如下：

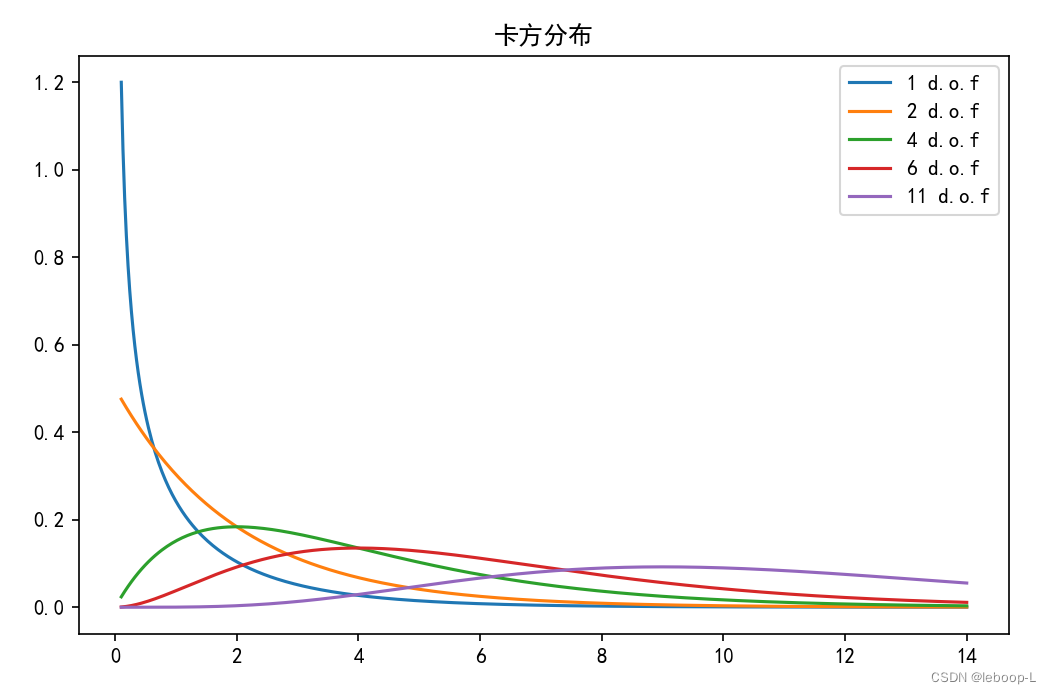
F分布

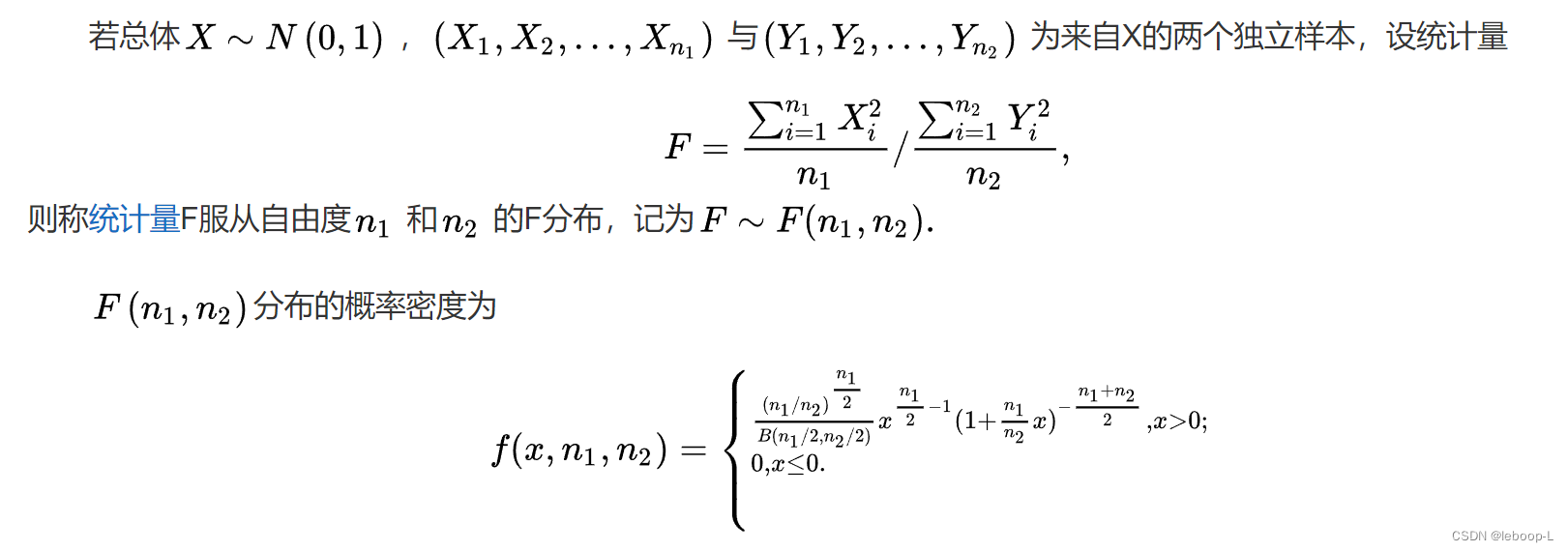
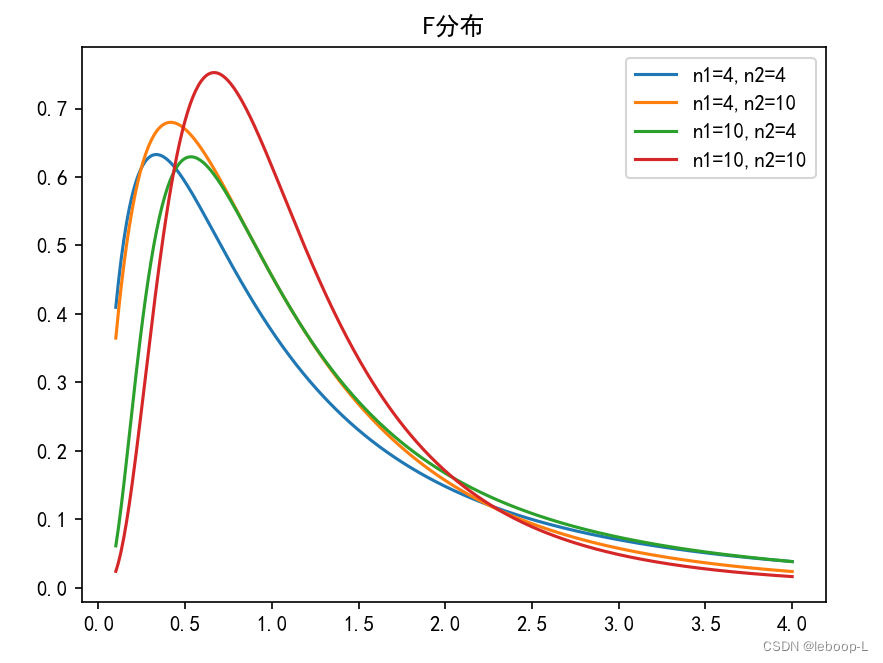
由卡方分布的定义知道，F分布定义可以转换为：如果 $X\sim \chi^2(n_1)$ , $Y\sim \chi^2(n_2)$ ,则

$F=\frac{X}{n_1}/\frac{Y}{n_2}$ 为F分布。概率密度函数的证明参见参考文献。

代码如下：

    X = np.linspace(0.1, 4, 500)plt.plot(X, stats.f.pdf(X, 4,4), label="n1=4,n2=4")plt.plot(X, stats.f.pdf(X, 4,10), label="n1=4,n2=10")plt.plot(X, stats.f.pdf(X, 10,4), label="n1=10,n2=4")plt.plot(X, stats.f.pdf(X, 10,10), label="n1=10,n2=10")plt.title("F分布")plt.legend()plt.show()

运行结果如下：

t分布

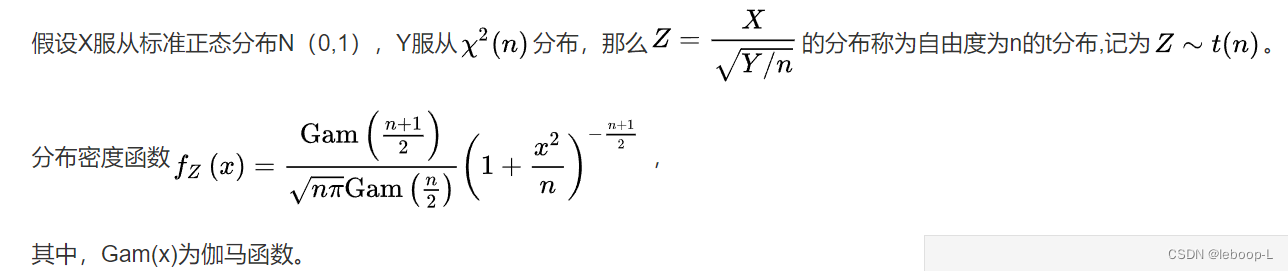
代码如下：

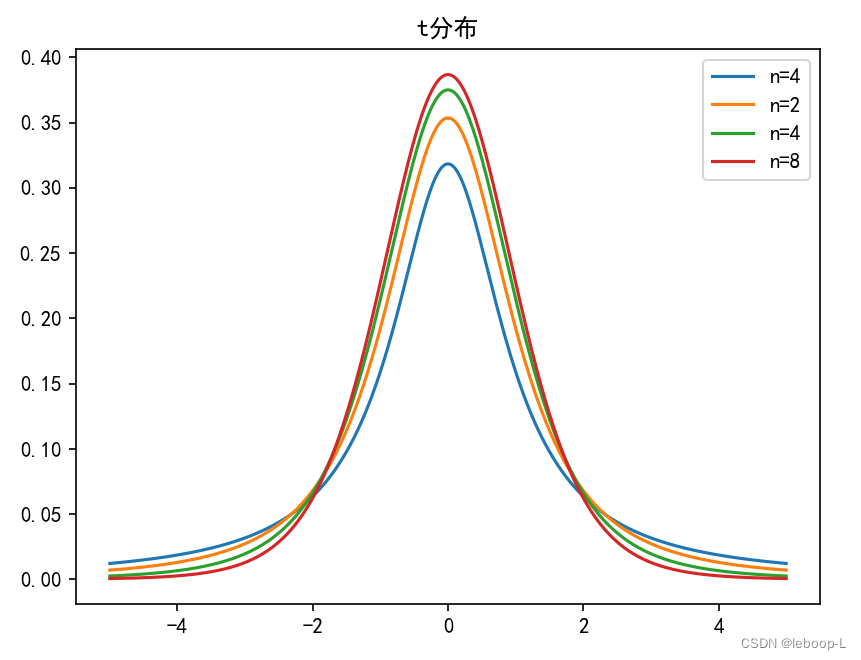
    plt.rcParams["axes.unicode_minus"] = False  # 设置显示中文后,负号显示受影响,显示负号X = np.linspace(-5, 5, 1500)plt.plot(X, stats.t.pdf(X, 1), label="n=4")plt.plot(X, stats.t.pdf(X, 2), label="n=2")plt.plot(X, stats.t.pdf(X, 4), label="n=4")plt.plot(X, stats.t.pdf(X, 8), label="n=8")plt.title("t分布")plt.legend()plt.show()

运行结果如下：

附录

本节所有代码如下：

import numpy as np
from scipy.special import beta
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# 创建一个网格x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))print('x=', '\n', x)print('y=', '\n', y)z = beta(x, y)print('z=', '\n', z)plt.rcParams['font.sans-serif'] = ['Simhei']  # 显示中文fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')ax.tick_params(axis="both", labelsize=12)ax.plot_surface(x, y, z, cmap='viridis')ax.set_xlabel('x', fontsize=13)ax.set_ylabel('y', fontsize=13)ax.set_zlabel('z')ax.set_title('贝塔函数图像')plt.show()X = np.linspace(0.1, 14, 500)plt.subplots(figsize=(8, 5))plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=4), label="4 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=6), label="6 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=11), label="11 d.o.f")plt.title("卡方分布")plt.legend()plt.show()X = np.linspace(0.1, 4, 500)plt.plot(X, stats.f.pdf(X, 4,4), label="n1=4,n2=4")plt.plot(X, stats.f.pdf(X, 4,10), label="n1=4,n2=10")plt.plot(X, stats.f.pdf(X, 10,4), label="n1=10,n2=4")plt.plot(X, stats.f.pdf(X, 10,10), label="n1=10,n2=10")plt.title("F分布")plt.legend()plt.show()plt.rcParams["axes.unicode_minus"] = False  # 设置显示中文后,负号显示受影响,显示负号X = np.linspace(-5, 5, 1500)plt.plot(X, stats.t.pdf(X, 1), label="n=4")plt.plot(X, stats.t.pdf(X, 2), label="n=2")plt.plot(X, stats.t.pdf(X, 4), label="n=4")plt.plot(X, stats.t.pdf(X, 8), label="n=8")plt.title("t分布")plt.legend()plt.show()

参考文献

高数篇（一）-- Gamma 函数 VS Beta 函数

极坐标与直角坐标二重积分转换

F分布概率密度函数的推导

python绘制正态分布及三大抽样分布的概率密度图像

这篇关于一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等

正态分布

对数正态分布

伽马分布

伽马函数

贝塔函数

伽马分布

卡方分布

$f(x,n)=\frac{x^{\frac{n}{2}-1}e^{-\frac{x}{2}}}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}$

F分布

t分布

附录

参考文献

相关文章

Java Spring 中 @PostConstruct 注解使用原理及常见场景

SQL中redo log 刷⼊磁盘的常见方法

SQL BETWEEN 的常见用法小结

python中各种常见文件的读写操作与类型转换详细指南

C++中初始化二维数组的几种常见方法

前端下载文件时如何后端返回的文件流一些常见方法

C++ vector的常见用法超详细讲解

Pytest多环境切换的常见方法介绍

C/C++错误信息处理的常见方法及函数

Go标准库常见错误分析和解决办法