本文主要是介绍力扣第101题 c++ 递归 迭代 双方法 +注释 ~,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目
101. 对称二叉树
简单
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
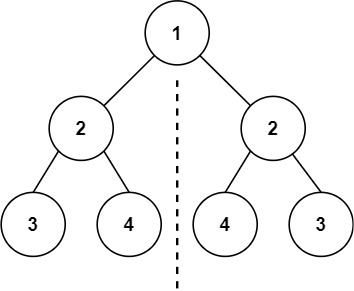
输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
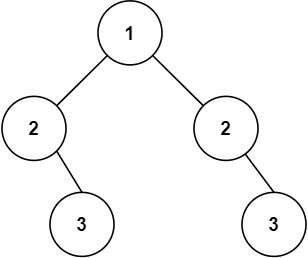
输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
进阶:你可以运用递归和迭代两种方法解决这个问题吗?
思路和解题方法一(递归)
compare()函数是用来判断两个节点是否对称的,其中left和right参数分别代表左右子节点。首先我们需要判断
left和right是否为空,若其中一个节点为空而另一个不为空,那么这两个节点不对称,返回false。如果两个节点都为空,则认为它们对称,返回true。如果两个节点的值不相等,则说明它们不对称,返回
false。如果两个节点的值相等,则需要递归判断它们的左右子节点是否对称。具体来说,需要比较左子树的左子节点和右子树的右子节点、左子树的右子节点和右子树的左子节点是否对称,即
outside = compare(left->left, right->right)和inside = compare(left->right, right->left)。最后,给出判断结果,即只有当左子树的左子节点和右子树的右子节点、左子树的右子节点和右子树的左子节点都对称时,才可以认为这两个节点对称,返回
isSame = outside && inside。
isSymmetric()函数是判断整个二叉树是否对称的。如果给定的根节点root为空,则直接返回true。否则,调用compare()函数比较根节点的左右子节点是否对称。最后,整个程序返回的是
isSymmetric()函数的返回值。
复杂度
时间复杂度:
O(n)
时间复杂度是O(n),其中n为二叉树的节点数,因为我们需要遍历每个节点,每个节点都需要进行一次比较。
空间复杂度
O(n)
空间复杂度也是O(n),因为在递归调用
compare()函数时,需要不断开辟新的栈空间来存储递归函数的参数和局部变量,最坏的情况下需要递归到最深层,此时栈空间的大小为O(n)。
c++ 代码
//复杂简单版
class Solution {
public:// 判断节点是否对称的函数bool compare(TreeNode* left, TreeNode* right) {// 首先排除空节点的情况if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;// 排除了空节点,再排除数值不相同的情况else if (left->val != right->val) return false;// 此时就是:左右节点都不为空,且数值相同的情况// 此时才做递归,做下一层的判断bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)return isSame;}// 判断整棵二叉树是否对称的函数bool isSymmetric(TreeNode* root) {if (root == NULL) return true;// 如果根节点不为空,调用compare()函数比较左子节点和右子节点是否对称return compare(root->left, root->right);}
};//精简版
class Solution {
public:// 检查两个节点是否对称的函数bool check(TreeNode *p, TreeNode *q) {// 如果两个节点都为空,视为对称if (!p && !q) return true;// 如果其中一个节点为空,另一个节点非空,视为不对称if (!p || !q) return false;// 检查当前节点的值是否相等,并递归检查左子树和右子树是否对称return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);}// 判断整棵二叉树是否对称的函数bool isSymmetric(TreeNode* root) {// 调用check函数,同时传入相同的根节点,判断左子树和右子树是否对称return check(root, root);}
};
思路和解题方法二(迭代)
首先检查根节点是否为空,若为空直接返回true。
创建一个队列que,并将根节点的左子树和右子树头结点依次加入队列。
进入while循环,判断队列是否为空。如果队列不为空,则继续执行循环体。
在循环体中,从队列中取出两个节点:leftNode为队列首部的节点,rightNode为队列次首部的节点。
判断左节点和右节点是否都为空。如果是,说明当前节点属于对称的部分,继续循环。
如果左节点和右节点有一个为空,或者它们的值不相等,返回false,表示不对称。
如果左节点和右节点都不为空且值相等,将其左孩子、右孩子按顺序依次加入队列,以备后续判断是否对称。
循环结束后,返回true,表示二叉树是对称的。
复杂度
时间复杂度:
O(n)
时间复杂度为O(n),其中n是二叉树的节点数。
空间复杂度
O(n)
使用了一个队列来存储节点,因此,空间复杂度为O(n)。
c++ 代码
class Solution {
public:bool isSymmetric(TreeNode* root) { // 判断二叉树是否对称的函数,传入根节点rootif (root == NULL) return true; // 如果根节点为空,返回truequeue<TreeNode*> que; // 创建一个队列que来存储需要判断的节点que.push(root->left); // 将左子树头结点加入队列que.push(root->right); // 将右子树头结点加入队列while (!que.empty()) { // 当队列不为空时,进行循环TreeNode* leftNode = que.front(); que.pop(); // 取出队列首部的节点leftNodeTreeNode* rightNode = que.front(); que.pop(); // 取出队列次首部的节点rightNodeif (!leftNode && !rightNode) { // 如果左节点为空、右节点为空,说明是对称的,继续循环continue;}// 左右一个节点不为空,或者都不为空但数值不相同,返回falseif ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {return false; // 如果左右节点有一个为空或者值不相等,直接返回false,表示当前二叉树不对称}// 加入左节点左孩子、右节点右孩子、左节点右孩子、右节点左孩子que.push(leftNode->left); // 左节点的左孩子que.push(rightNode->right); // 右节点的右孩子que.push(leftNode->right); // 左节点的右孩子que.push(rightNode->left); // 右节点的左孩子}return true; // 当循环结束时,说明整个二叉树都对称,返回true}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
这篇关于力扣第101题 c++ 递归 迭代 双方法 +注释 ~的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






