函数格式 scipy.optimize. linprog ( c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='simplex', callback=None, options=None ) 今天阅读数据建模第一章线性规划问题，问题描述如下： 
通过介绍我们知道了线性规划，就是目标函数及约束条件均为线性函数。 
通过画图我们可知，X1，X2的最优解为2，6，目标值为26。 我们如何时候这个scipy的公式来计算这个值呢:
>>> c = [-1, 4] >>> A = [[-3, 1], [1, 2]] >>> b = [6, 4] >>> x0_bounds = (None, None) >>> x1_bounds = (-3, None) >>> from scipy.optimize import linprog >>> res = linprog(c, A_ub=A, b_ub=b, bounds=(x0_bounds, x1_bounds), ... options={"disp": True}) >>> print(res) Optimization terminated successfully. Current function value: -11.428571 Iterations: 2 status: 0 success: True fun: -11.428571428571429 x: array([-1.14285714, 2.57142857]) message: 'Optimization terminated successfully.' nit: 2
上面是官方给出的案例，我们很难看出来这个怎么求解最大值，不过英语好的也可以把。 言归正传，我们先结合官网是思路得出最小值的解。
In [1]:c = np.array([4,3])
In [1]:a = np.array([[2,1],[1,1]])
In [1]:In [1]:b = np.array([10,8])
In [1]:optimize.linprog(c,a,b,bounds=((0,None),(0,7)))
Out[1]:
fun: -0.0
message: 'Optimization terminated successfully.'
nit: 0
slack: array([ 10., 8., 7.])
status: 0
success: True
x: array([ 0., 0.])
按照正常的计算 我们得出了最小值为0，且x的两个值为 0 ， 0。对于上面的的公式有必要说明的是，bounds是针对x的最大最小一次给一个值，从题目可知，x1的取值范围为大于0，最小值就为0，最大值没有约束，被其他的条件所约束就可以了 ，没有明确，所以是写的 （0，None）,而相对x2来说，他最小值为0，最大值被C约束，为7。所以范围为（0，7），当有三个求解的时候，依次增加，不可省略。 接下来我们说这个最大值怎么求，其实只要对C取反我们就可以求除最大值的负数，对结果在取反回来就可以了
In [1]:optimize.linprog(-c,a,b,bounds=((0,None),(0,7)))
Out[1]:
fun: -26.0
message: 'Optimization terminated successfully.'
nit: 2
slack: array([ 0., 0., 1.])
status: 0
success: True
x: array([ 2., 6.])
是不是很简单，得到的-26取反回来就是我们的最大值求解了，（2，6）就是我们的X1,X2取值了。其实有时候那个条件为>,>=的时候我们要写成<,<=的模式，一样对参数和结果取反就行了。 我这里在补充一个求三个解的实例：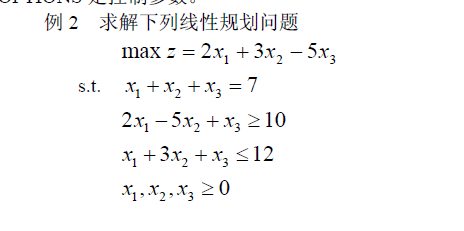 
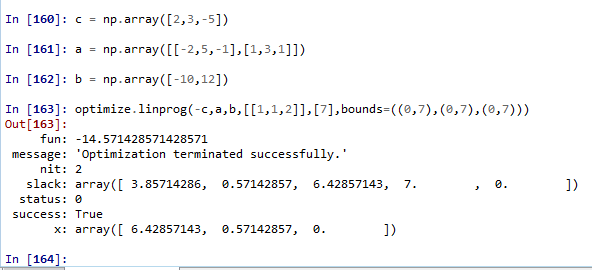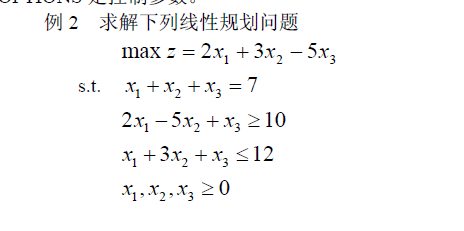
我们的最优解为 14.57
