本文主要是介绍优化方法的应用(optimtool.example),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
import optimtool as oo
from optimtool.base import np, sp, plt
pip install optimtool>=2.4.2
优化方法的应用(optimtool.example)
import optimtool.example as oe
Lasso问题(Lasso)
oe.Lasso.[函数名]([矩阵A], [矩阵b], [因子mu], [参数表], [初始迭代点])
min 1 2 ∣ ∣ A x − b ∣ ∣ 2 + μ ∣ ∣ x ∣ ∣ 1 \min \frac{1}{2} ||Ax-b||^2+\mu ||x||_1 min21∣∣Ax−b∣∣2+μ∣∣x∣∣1
给定 A m × n A_{m \times n} Am×n, x n × 1 x_{n \times 1} xn×1, b m × 1 b_{m \times 1} bm×1,正则化常数 μ \mu μ。解决该无约束最优化问题,该问题目标函数一阶不可导。
| 方法头 | 解释 |
|---|---|
| gradient(A: NDArray, b: NDArray, mu: float, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, delta: float=10, alp: float=1e-3, epsilon: float=1e-2, k: int=0) -> OutputType | 光滑化Lasso函数法 |
| subgradient(A: NDArray, b: NDArray, mu: float, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, alphak: float=2e-2, epsilon: float=1e-3, k: int=0) -> OutputType | 次梯度法Lasso避免一阶不可导 |
| approximate_point(A: NDArray, b: NDArray, mu: float, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, epsilon: float=1e-4, k: int=0) -> OutputType | 邻近算子更新 |
import scipy.sparse as ss
x = sp.symbols('x1:9')
m, n = 4, 8
u = (ss.rand(n, 1, 0.1)).toarray()
Mu = 1e-3
A = np.random.randn(m, n)
b = np.random.randn(m, n).dot(u)
x_0 = tuple([1 for _ in range(8)])
oe.Lasso.subgradient(A, b, Mu, x, x_0, verbose=False)
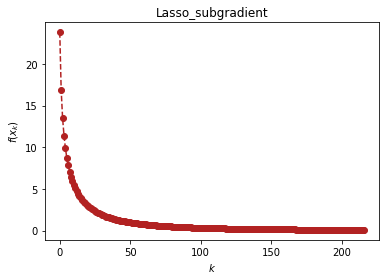
(array([ 0.31938837, -0.01063285, 0.64248879, 0.39738588, -0.59341723, -0.20835098, 0.65554228, 0.44903602]), 216)
曲线相切问题(WanYuan)
oe.WanYuan.[函数名]([直线的斜率], [直线的截距], [二次项系数], [一次项系数], [常数项], [圆心横坐标], [圆心纵坐标], [初始迭代点])
问题描述:
给定直线的斜率和截距,给定一个抛物线函数的二次项系数,一次项系数与常数项。 要求解一个给定圆心的圆,该圆同时与抛物线、直线相切,若存在可行方案,请给出切点的坐标。
| 方法头 | 解释 |
|---|---|
| solution(m: float, n: float, a: float, b: float, c: float, x3: float, y3: float, x_0: tuple, verbose: bool=False, draw: bool=False, eps: float=1e-10) -> str | 使用高斯-牛顿方法求解构造的7个残差函数 |
oe.WanYuan.solution(1, 2, 0.2, -1.4, 2.2, 3, -2.5, (4, 4, -4, -2, -2, 4), True)
(4, 4, -4, -2, -2, 4) 61612.182500000024 0
[ 3.29133755 0.06740836 -2.5150997 0.28351846 1.0655889 -0.94429557] 13380.08160556542 1
[-1.11968963 -3.58590014 -2.69274677 -1.37736125 -0.26164182 -0.77291041] 1198.7999458909264 2
[-0.30266852 -2.89871252 -2.59053473 -0.61494902 1.62333363 -0.18803779] 1.5198302153861234 3
[-0.09044295 -2.47519749 -2.22330715 -0.34428703 1.67765088 0.02982181] 0.3269218137297747 4
[-0.04674173 -2.3650673 -2.16182829 -0.25144656 1.69657453 0.11211081] 0.23257960438227657 5
[ 0.00834682 -2.21605565 -2.09213868 -0.11631022 1.72502288 0.23298958] 0.1283472579162907 6
[ 0.04441602 -2.1008148 -2.06090762 0.00449731 1.7522343 0.34204307] 0.010358309290037107 7
[ 0.03898432 -2.11262103 -2.07069068 -0.00294621 1.75120302 0.33509119] 0.002797404047207694 8
[ 0.03915084 -2.11208603 -2.07046856 -0.00246663 1.75127154 0.33557915] 0.002796695858338408 9
[ 0.03914121 -2.11211464 -2.07048258 -0.00249084 1.75126809 0.33555454] 0.0027966954396675928 10
[ 0.03914172 -2.11211313 -2.07048185 -0.00248957 1.75126827 0.33555584] 0.0027966954385178202 11
[ 0.03914169 -2.11211321 -2.07048189 -0.00248963 1.75126826 0.33555577] 0.0027966954385146964 12
[ 0.03914169 -2.11211321 -2.07048189 -0.00248963 1.75126826 0.33555577] 0.0027966954385146483 13
[ 0.03914169 -2.11211321 -2.07048189 -0.00248963 1.75126826 0.33555577] 0.002796695438514672 14
[ 0.03914169 -2.11211321 -2.07048189 -0.00248963 1.75126826 0.33555577] 0.0027966954385146175 15
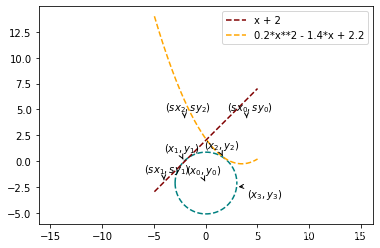
'(x0, y0)=(0.04, -2.11), (x1, y1)=(-2.07, -0.0), (x2, y2)=(1.75, 0.34)'
这篇关于优化方法的应用(optimtool.example)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







