本文主要是介绍【408数据结构】散列 (哈希)知识点集合复习考点题目,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

苏泽
“弃工从研”的路上很孤独,于是我记下了些许笔记相伴,希望能够帮助到大家
知识点
1. 散列查找
散列查找是一种高效的查找方法,它通过散列函数将关键字映射到数组的一个位置,从而实现快速查找。这种方法的时间复杂度平均为(O(1)),但最坏情况下可能会退化到(O(n))。
3. 散列函数
散列函数是散列存储的核心,其设计需要考虑关键字的分布情况和冲突概率。
- 散列查找是典型的"用空间换时间"的算法,只要散列函数设计的合理,散列表越长,冲突的概率越 低
- 除留余数法,即H(key) = key % p
- 直接定址法
H(key) = a * key + b
适合关键字分布基本连续的情况,如果关键字不连续,空位太多会造成存储空间的浪费- 数字分析法
选取分布较为均匀的若干位作为散列地址- 平方取中法
取关键字的平方值的几位作为散列地址。
适合散列地址与关键字的每位都有关系
4. 冲突处理
冲突是散列存储中不可避免的问题。处理冲突的方法主要有开放定址法和链地址法。开放定址法通过在表中寻找空闲位置来解决冲突,而链地址法则通过将具有相同散列地址的元素链接成一个链表来处理冲突。
- 开放地址法:
线性探测法
发生冲突的时候,每次往后探测相邻的下一个单元是否为空
进行查找的时候,通过散列函数得到Hi并依次比较,如果遇到空则说明查找失败
删除结点不能简单的将被删结点的空间置为空,否则将阶段在它之后填入散列表的同义词的查找路径,而可以做一个删除标记进行逻辑删除 - 平方探测法比起线性探测表更不容易产生聚集堆积问题
- 伪随机序列法
一个伪随机序列
题目
1. 散列查找的缺点是什么?
解答:
散列查找的缺点主要表现在以下几个方面:
- 可能会产生冲突,需要解决冲突的方法。
- 冲突处理方法(如链地址法)会增加额外的空间开销。
- 在最坏情况下(所有元素都冲突),查找时间复杂度会退化到 (O(n))。
2. 什么是散列存储?
解答:
散列存储是一种数据结构,它根据关键码值(Key Value)直接进行访问。通过Hash函数将要查找的项与表的一个位置关联,以加快查找的速度。它是一种“用空间换时间”的算法,只要散列函数设计的合理,散列表越长,冲突的概率越低。
3. 散列存储适用于什么情况?
解答:
散列存储适用于以下情况:
- 数据量大,且查找操作较多。
- 可以接受一定程度的冲突。
- 需要快速查找、插入和删除操作。
4. 散列查找的时间复杂度与什么有关?
解答:
散列查找的时间复杂度主要与以下因素有关:
- 散列表的长度(m):散列表越长,冲突的概率越低。
- 冲突概率:冲突越少,查找效率越高。
- 散列函数的设计:合理的散列函数可以减少冲突,提高查找效率。
5. 散列函数的设计需要考虑哪些因素?
解答:
散列函数的设计需要考虑以下因素:
- 关键字的分布情况:散列函数应该能够将关键字均匀地分布在散列表中,减少冲突。
- 冲突概率:设计散列函数时应该尽量减少冲突的概率。
- 计算效率:散列函数的计算应该尽可能简单高效,以减少查找和插入的时间。
6. 什么是开放地址法?
解答:
开放地址法是一种处理散列冲突的方法。当发生冲突时,它会选择一个开放的散列地址,将元素存入该地址。开放地址法的实现方式包括线性探测法、二次探测法和双重散列法等。
7. 什么是再散列?
解答:
再散列是一种解决哈希冲突的方法。当发生冲突时,通过一定的计算找到一个新的位置来存储数据。再散列可以提高散列表的查找效率,避免堆积现象。
8. 散列查找的平均查找复杂度是多少?
解答:
散列查找的平均查找复杂度是 (O(1))。这是因为在理想情况下,散列函数可以将关键字均匀地分布在散列表中,每个关键字只需要一次查找就可以找到对应的存储位置。
9. 散列表的空间复杂度是多少?
解答:
散列表的空间复杂度是 (O(n))。为了减少冲突,通常需要设计一个足够长的散列表,其长度与存储的元素数量成正比。
10. 如何解决哈希表中的冲突?
解答:
解决哈希表中的冲突的方法主要包括:
- 链地址法:将具有相同散列地址的元素存储在一个链表中。
- 开放地址法:当发生冲突时,选择一个开放的散列地址,将元素存入该地址。
- 再散列法:通过更换散列函数或调整散列表的大小来减少冲突
另外,利用了工作之余的一点点时间,整理了一套考研408的知识图谱,
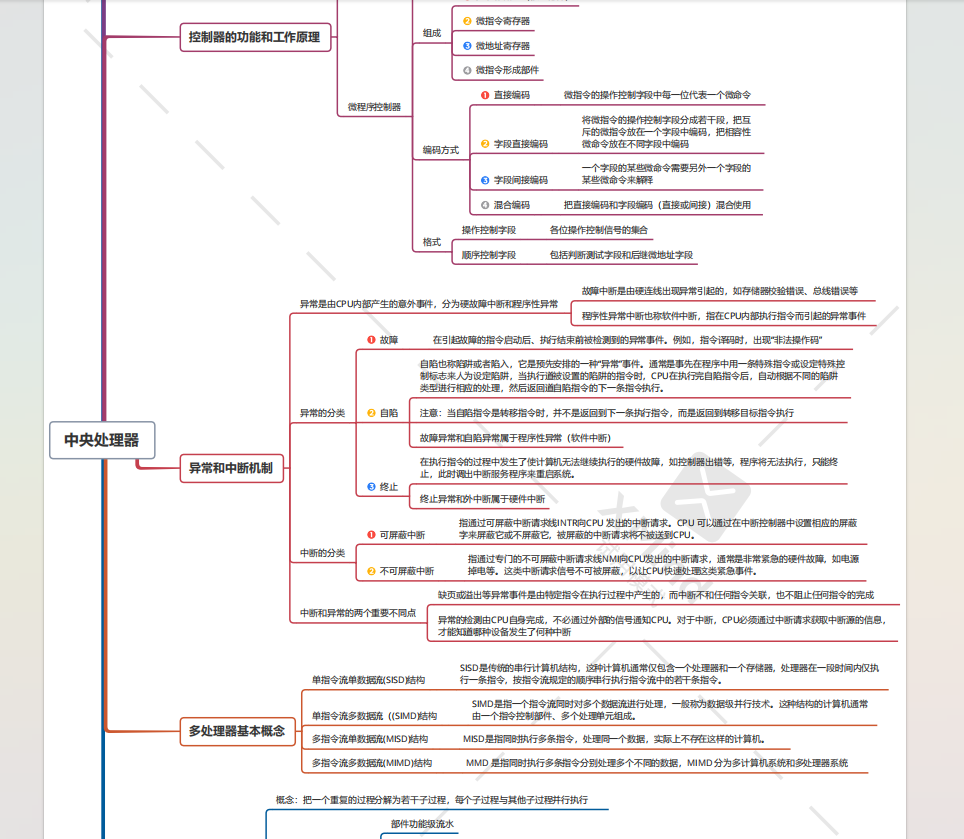
我根据这一套知识图谱打造了这样一个408知识图谱问答系统
里面的每一个回答都是根据考研408的考点回复的

目前暂时只接入了微信,如果大家对这个问答系统感兴趣的话可以在我的主页里找到我的微信号
找我拉进测试群免费体验哦
这篇关于【408数据结构】散列 (哈希)知识点集合复习考点题目的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








