强化学习深入学习（一）：价值函数和贝尔曼方程

本文主要是介绍强化学习深入学习（一）：价值函数和贝尔曼方程，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

0. 引言

强化学习（Reinforcement Learning, RL）是一种机器学习方法，通过与环境的交互来学习如何采取行动，以最大化累积的回报。智能体的目标是找到最优策略 ${\pi }^{\ast }$，使得从任意状态 $s$ 开始行动时，累积的期望回报最大。这个问题通常通过优化策略的方式来解决。

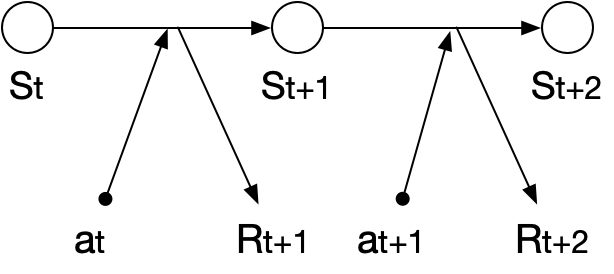
强化学习的基本概念

• 智能体（Agent）: 强化学习的核心参与者，它通过与环境交互，选择行动并从中学习。智能体的目标是找到一个策略，使得在长期内获得的累积回报最大化。

• 环境（Environment）: 智能体所处的外部世界。智能体与环境交互，通过执行动作改变环境状态，并接收来自环境的反馈（奖励和新状态）。

• 状态（State, $s$）: 环境在某一时刻的具体情况或描述。状态可以是环境的完整描述，也可以是部分信息的表示。

• 动作（Action, $a$）: 智能体在每个状态下可以采取的操作。动作会影响环境的状态，并引发反馈。

• 奖励（Reward, $r$）: 环境对智能体采取某一动作的反馈。奖励是一个标量值，用于指示该动作的好坏。智能体的目标是最大化累积奖励。

• 策略（Policy, $\pi$）: 智能体在每个状态下选择动作的规则或分布。策略可以是确定性的（在某状态下总是选择同一动作）或随机的（在某状态下根据概率选择动作）。

• 回报（Return, $G$）: 从某一时刻开始，智能体获得的累积奖励。通常使用折扣因子 $\gamma$ 来对未来的奖励进行折扣计算。

强化学习的工作流程

1. 初始状态: 智能体从环境中感知当前的状态 $s_t$。

2. 动作选择: 基于当前策略 $\pi$，智能体选择一个动作 $a_t$。

3. 执行动作: 智能体执行动作 $a_t$，该动作影响环境并导致状态转移。

4. 反馈接收: 环境反馈给智能体一个奖励 $r_{t+1}$ 以及新的状态 $s_{t+1}$。

5. 更新策略: 智能体利用获得的反馈更新策略，使得将来在类似情形下能做出更好的选择。

6. 重复: 过程重复，直到智能体达到目标或学习结束。

1. 回报（Return）

回报是指在某个状态下开始，经过一系列行动后获得的累积奖励（Reward）。在时间步 $t$ 时的回报通常表示为 $G_t$。

对于无折扣的情况，总回报为：
$$G_t=R_{t+1}+R_{t+2}+R_{t+3}+\cdots =\sum _{k=0}^{\infty }{R}_{t+k+1}$$

如果使用折扣因子 $\gamma$（其中 $0\le \gamma \le 1$）来表示未来奖励的重要性，回报可以表示为：
$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots =\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$$

这里，$\gamma$ 控制了未来奖励对当前回报的影响程度。当 $\gamma$ 越接近 1，越更加重视长期奖励；当 $\gamma$ 越接近 0，则更加关注短期奖励。

2. 价值函数（Value Function）

价值函数用来评估一个状态或状态-动作对的好坏。价值函数有两种主要形式：

（1）状态价值函数（State Value Function, $V(s)$）：表示在状态 $s$ 下，按照某一策略 $\pi$ 行动时，未来回报的期望值。
$$V_{\pi }(s)={\mathbb{E}}_{\pi }\left[G_t\mid S_t=s\right]={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\mid S_t=s\right]$$

（2）动作价值函数（Action Value Function, $Q(s,a)$）：表示在状态 $s$ 下采取动作 $a$ 并且随后按照某一策略 $\pi$ 行动时，未来回报的期望值。
$$Q_{\pi }(s,a)={\mathbb{E}}_{\pi }\left[G_t\mid S_t=s,A_t=a\right]$$

下面说明状态价值函数 $V_{\pi }(s)$ 和动作价值函数 $Q_{\pi }(s,a)$ 之间通过策略 $\pi$ 联系在一起。$V_{\pi }(s)$ 可以被视为在当前状态下所有可能动作的 $Q_{\pi }(s,a)$ 的加权平均。

3. 贝尔曼期望方程（Bellman Expectation Equation）

贝尔曼期望方程将价值函数表示为当前奖励与未来状态的价值之间的关系。

（1）状态价值函数的贝尔曼期望方程：
$$V_{\pi }(s)={\mathbb{E}}_{\pi }\left[R_{t+1}+\gamma V_{\pi }(S_{t+1})\mid S_t=s\right]$$
这表示在状态 $s$ 下的价值等于当前行动得到的即时奖励与未来状态的折扣价值的期望值。

（2）动作价值函数的贝尔曼期望方程：
$$Q_{\pi }(s,a)=\mathbb{E}\left[R_{t+1}+\gamma {\mathbb{E}}_{\pi }\left[Q_{\pi }(S_{t+1},A_{t+1})\mid S_{t+1}\right]\mid S_t=s,A_t=a\right]$$
这里，$Q_{\pi }(s,a)$ 表示在状态 $s$ 下采取动作 $a$ 后，立即获得的奖励加上下一状态的期望价值。

4. 贝尔曼最优方程（Bellman Optimality Equation）

贝尔曼最优方程用于描述最优策略下的状态或动作的价值。

（1）最优状态价值函数的贝尔曼方程：
$$V_{\ast }(s)=\underset{a}{\max }\mathbb{E}\left[R_{t+1}+\gamma V^{\ast }(S_{t+1})\mid S_t=s,A_t=a\right]$$
这意味着在最优策略下，状态 $s$ 的价值是通过选择在该状态下的最佳行动所获得的即时奖励和后续状态的最优价值来决定的。

（2）最优动作价值函数的贝尔曼方程：
$$Q_{\ast }(s,a)=\mathbb{E}\left[R_{t+1}+\gamma \underset{a^{\prime }}{\max }{Q}^{\ast }(S_{t+1},a^{\prime })\mid S_t=s,A_t=a\right]$$
这里，$Q_{\ast }(s,a)$ 表示在状态 $s$ 下采取动作 $a$ 后，立即获得的奖励加上后续状态的最优行动价值。

总结

（1）回报 $G_t$ 是从某个时间步开始所能获得的累积奖励。

（2）价值函数 $V(s)$ 和 $Q(s,a)$ 用于评估状态或动作的长期好坏。

（3）贝尔曼期望方程 将价值函数与未来的期望回报联系起来，表达策略下的期望价值。

（4）贝尔曼最优方程 则用于找到最优策略下的最大期望回报。

---

欢迎关注本人，我是喜欢搞事的程序猿； 一起进步，一起学习；

欢迎关注知乎/CSDN：SmallerFL

也欢迎关注我的wx公众号（精选高质量文章）：一个比特定乾坤

这篇关于强化学习深入学习（一）：价值函数和贝尔曼方程的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---