本文主要是介绍计算图片中的物体的实际尺寸的一种方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
计算图片中的物体的实际尺寸的一种方法
图像测量利用了摄像头成像也就是小孔成像的几个性质[2]:
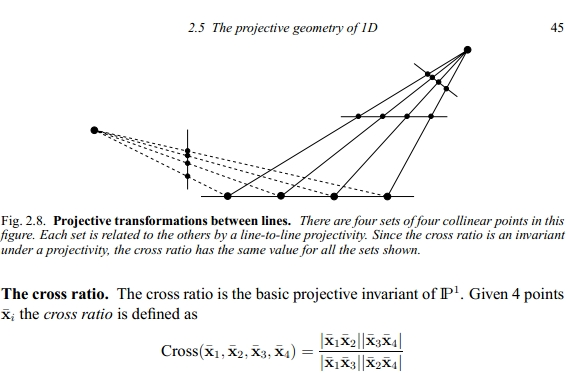
第一,摄像头把平行的直线映射为图像上相交直线,笔直的铁轨在远处相交就是这个道理,这个交点被称为消隐点(vanish point)。可以认为平行空间直线在无穷远处相交,消隐点则是这一交点的像。所有水平的平行直线族都各自相交于无穷远处的一点,这些点构成无穷远直线,这条直线在图像上的像叫地平线。我们所居住的三维空间中存在三组相互垂直的直线(例如水平两组,x轴和y轴方向,竖直一组,z轴方向),所有x、y、z方向上的平行直线在一张图片上会分别相交于各自的一个消隐点。并且水平直线对应的两个消隐点如果连起来,连线就是地平线。测量的关键,就是要得到这些消隐点,因此有很多竖直线(如书架)或水平线(如地板砖)的图片就容易测量。
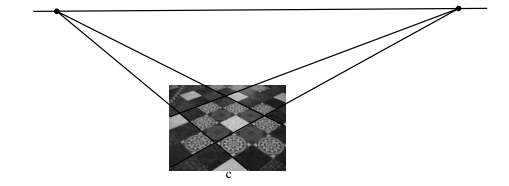
第二,摄像头把三维空间投影到二维的图像上,保持直线交比不变,交比是四个点两两“比例的比例”。所以如果在三维空间中的一条直线上有四个点,那么它们映射到图片上的四个点后,这四个点的交比不变。
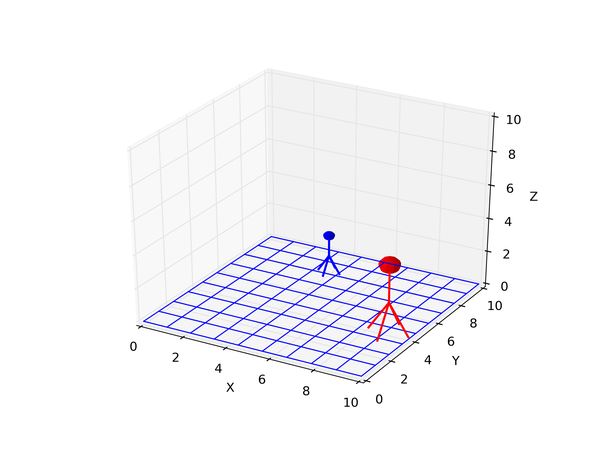
首先,假设我们已知蓝色小人Bob的身高,要求出红色小人John的身高,只需要知道两人的身高比值就可以:
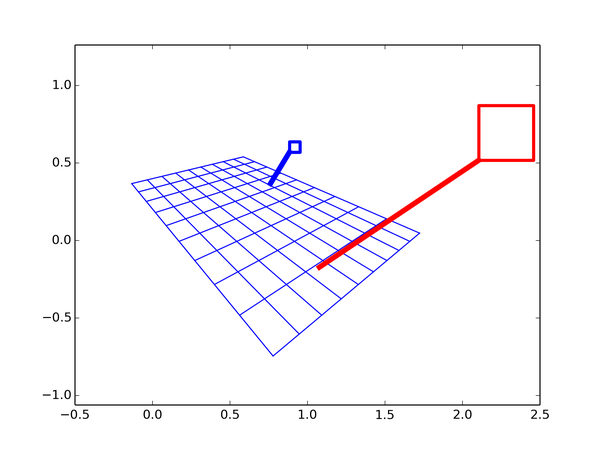
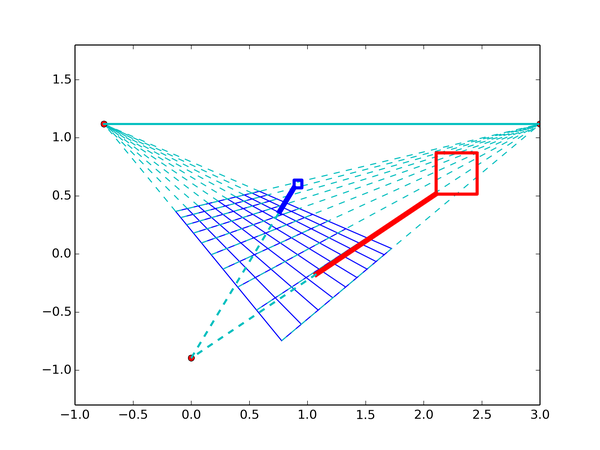
我们用大写字母表示真实的坐标,随后用小写字母表示图片上的像素坐标。两人的身高比值BE/AF可以这么求:首先连接AB,然后过E点做AB的平行线交AF于点D,因为ABED是个矩形,所以要求的比值就等于AD/AF。然而,这种判断是在三维空间中做出的,当物体成像为图片,所有点的位置都会发生变化(不要问我圆头为什么会变成方头):
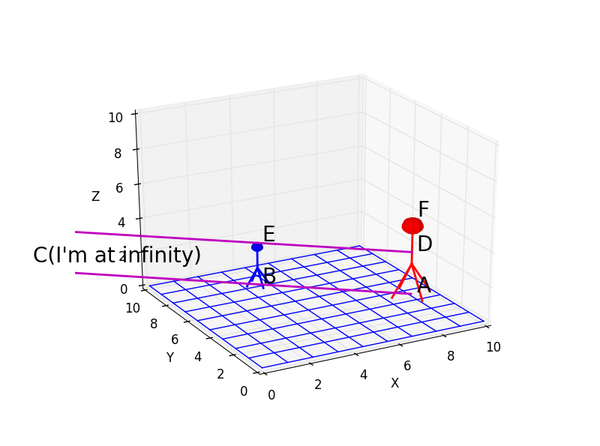
其中最显著的变化是平行线相交了,由此我们可以找到三个方向的消隐点,这可以通过对竖直和两组水平平行线求延长线获得:
注意我们把水平平行线对应的两个消隐点连接起来,得到了一条在(无穷)远处的直线,每个人都熟悉它,它就是地平线。地平线上所有的点都有一个性质:从其上一个点引出的所有直线都是相互水平平行的。
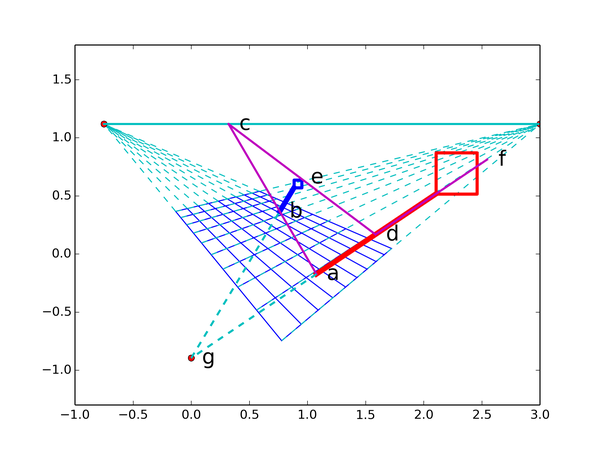
因此点D在图上的坐标d是这么求出的:
1. 画出地平线
2. 延长ab,交地平线于点c
3. 延长ce,交af,也就是John于点d
因为点c在无穷远处,所以cd和ca在空间中是平行直线,abed也就是上面说述真实空间中矩形ABED的像。
(转载者说明:如果cd也是水平面上一直线,那么cd和ca互相平行是正确的,但是本文中cd是不在水平面上的)
然而,知道了某些点在图像上的像,它们的实际长度比是无法直接从图上测得的,因为大家的深度不一样,这时就要利用成像前后一条直线上四个点交比不变的性质,考察红色小人John身上的三个点A、D、F以及其延长到无穷远处的点G,就可以得到(大写字母换成小写字母):
(AD/AF)/(GD/GF)=(ad/af)/(gd/gf)
因为已经求出了点d,等式右边所有的量都可以从图像上测出。等式左边的点G在真实空间是所有垂直直线的交点,这个点在无穷远,和无穷相比点F和点D的差异可以忽略不计,所以GD/GF=1,这样就得到最终结果:
AD/AF = (ad/af)/(gd/gf)
[1] Criminisi A, Reid I, Zisserman A. Single view metrology[J]. International Journal of Computer Vision, 2000, 40(2): 123-148.
[2] Hartley R, Zisserman A. Multiple view geometry in computer vision[M]. Cambridge university press, 2003.
这篇关于计算图片中的物体的实际尺寸的一种方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!