本文主要是介绍POJ 3468 A Simple Problem with Integers 树状数组 区间修改 区间查询,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目链接点这儿
给你一个数列,最多10W次操作,要么区间统一加上某个值,要么查询某个区间的和。
第一反应肯定是线段树,但是呢,这个能不能用树状数组做呢?
如果是单点修改,区间查询,我们直接在原数列上进行树状数组的操作。
如果是区间修改,单点查询。由于树状数组每次update一个单点x之后,会对n>x的getsum(n)(或者说树状数组的Query(n)操作)都有影响。也就是说,虽然修改的是单点,但对查询的影响是区间的。从而我们可以利用这个,在保持原数列不改变的同时另找一个树状数组来记录每个位置修改的值。如果在区间[i, j]每个值增加delta,那么我们可以通过update(i, delta), update(j+1, -delta)的操作来使getsum(pos)的值就是pos这个位置到这一时刻位置为止的改变量。从而查询i处的值的话,只需返回a[i] + getsum(i)(a[i]是该位置的初始值)。
那么现在要区间查询,仍然可以借助区间修改,单点查询的思路,但是我们还要求Σgetsum(i)(i >= left value, i <= right value),这个操作直接写明显会浪费很大力气。
我们记树状数组维护的那个数组为b[](也就是说这个数组满足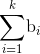
我们现在要求的是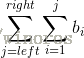
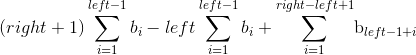
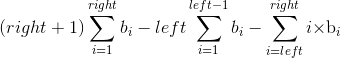
下面放出代码
- #include <vector>
- #include <list>
- #include <map>
- #include <set>
- #include <deque>
- #include <queue>
- #include <stack>
- #include <bitset>
- #include <algorithm>
- #include <functional>
- #include <numeric>
- #include <utility>
- #include <sstream>
- #include <iostream>
- #include <iomanip>
- #include <cstdio>
- #include <cmath>
- #include <cstdlib>
- #include <cctype>
- #include <string>
- #include <cstring>
- #include <cstdio>
- #include <cmath>
- #include <cstdlib>
- #include <ctime>
- #include <climits>
- #define up(i, lower, upper) for(int i = lower; i < upper; i++)
- #define down(i, lower, upper) for(int i = upper-1; i >= lower; i--)
- using namespace std;
- #define MAX_N 100010
- typedef pair<int, int> pii;
- typedef pair<double, double> pdd;
- typedef vector<int> vi;
- typedef vector<pii> vpii;
- typedef long long ll;
- typedef unsigned long long ull;
- const double pi = acos(-1.0);
- const double eps = 1.0e-9;
- template<class T>
- inline bool read(T &n){
- T x = 0, tmp = 1; char c = getchar();
- while((c < '0' || c > '9') && c != '-' && c != EOF) c = getchar();
- if(c == EOF) return false;
- if(c == '-') c = getchar(), tmp = -1;
- while(c >= '0' && c <= '9') x *= 10, x += (c - '0'),c = getchar();
- n = x*tmp;
- return true;
- }
- template <class T>
- inline void write(T n) {
- if(n < 0) {
- putchar('-');
- n = -n;
- }
- int len = 0,data[20];
- while(n) {
- data[len++] = n%10;
- n /= 10;
- }
- if(!len) data[len++] = 0;
- while(len--) putchar(data[len]+48);
- }
- struct BIT {
- ll sum[MAX_N];
- int len;
- BIT() {
- len = 0;
- memset(sum, 0, sizeof sum);
- }
- BIT(int len) : len(len) {
- memset(sum, 0, sizeof sum);
- }
- ll lowbit(ll x) { return x&(-x); }
- ll getsum(int n) {
- ll ans = 0;
- while(n > 0) ans+=sum[n], n-=lowbit(n);
- return ans;
- }
- void update(int pos, ll val) {
- while(pos <= len) sum[pos] += val, pos+=lowbit(pos);
- }
- };
- //-------------------------------------------------------
- BIT a, b;
- int main() {
- int n, m, l, r, val;
- ll sum[100010] = { 0 };
- char str[2];
- read(n), read(m);
- a.len = b.len = n;
- up(i, 1, n+1) read(val), sum[i] = sum[i-1] + val;
- up(i, 0, m) {
- scanf("%s", str);
- if(str[0] == 'C') {
- read(l), read(r), read(val);
- a.update(l, val), a.update(r+1, -val);
- b.update(l, val*l), b.update(r+1, -val*(r+1));
- }
- else {
- read(l), read(r);
- //printf("%lld", sum[r] - sum[l-1] + a.getsum(r)*(r+1) - a.getsum(l-1)*l - b.getsum(r) + b.getsum(l-1));
- write(sum[r] - sum[l-1] + a.getsum(r)*(r+1) - a.getsum(l-1)*l - b.getsum(r) + b.getsum(l-1));
- puts("");
- }
- }
- return 0;
- }
这篇关于POJ 3468 A Simple Problem with Integers 树状数组 区间修改 区间查询的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





