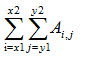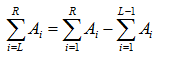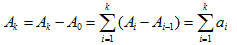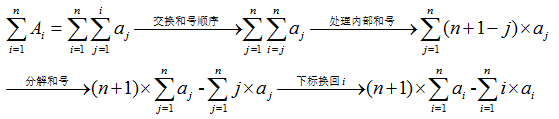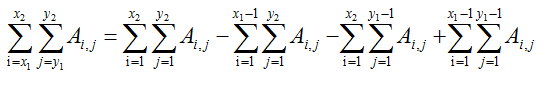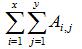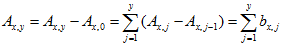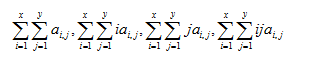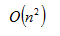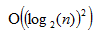本文主要是介绍树状数组实现矩阵中矩形区域的修改以及求和,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
树状数组实现矩形区域的修改以及求和
By 岩之痕
讲讲树状数组如何实现对一个矩阵的矩形区域的加法和求和。
以下,(x1,y1)为矩形的左下角坐标,(x2,y2)为矩形的右上角坐标(x1<=x2 , y1<=y2)。
矩形加法:Add(int x1,int y1,int x2,int y2,int K)表示给指定矩形区域的元素都加上K。
矩形求和:Sum(int x1,int y1,int x2,int y2) 即求
思路就是通过差分,化区间修改为点修改,然后用树状数组来解决。
由于要用到树状数组,以下所有数组下标都从1开始,并令A[0]=0,方便讨论。
先说说一维的情况:
对于一维数组A,要求区间和,首先化区间和为前缀和:
于是只需要讨论如何求前缀和(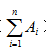
对于区间修改,直接用树状数组来维护A的前缀和是O(n)的时间复杂度。
树状数组只支持点修改,于是,想一想,怎么化区间修改为点修改?
考虑数组a[i]=A[i]-A[i-1](注意边界条件A[0]=0,所以i=1的时候这个式子也是符合的),
当A数组的区间[L,R]都加上K的时候,a数组只有两个值改变了,
a[L] 多了K ,a[R+1] 少了K,这就做到了化区间修改为点修改。
我们再来看看如何从a[i]来得到A[i]的前缀和。
首先注意到:
前缀和的计算如下:
扩展到二维的情况:
开始讲二维的情况:
类似一维情况中化区间和为前缀和之差的方法,有如下公式:
于是只需要解决这个问题:
思路当然还是差分,首先纵向差分:
令
于是:
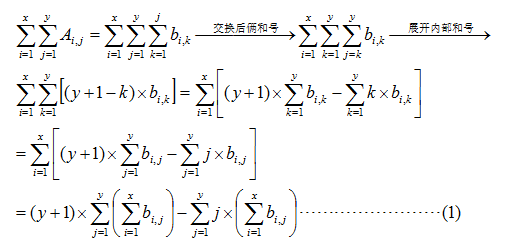
此时,b[i][j]+= t 代表的含义就是b[i][j],b[i][j+1],...,b[i][n]都增加了t.
也就是实现了纵向的化区间修改为点修改。
要修改一个矩形区域,也就是需要连续修改i在一个区间的b[i][j],于是将b[i][j]再横向差分,
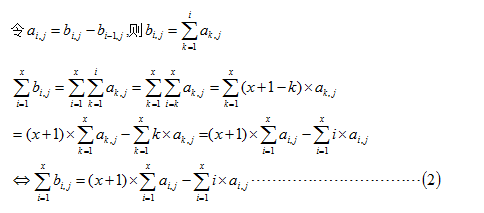
把(2)式代入(1)式:
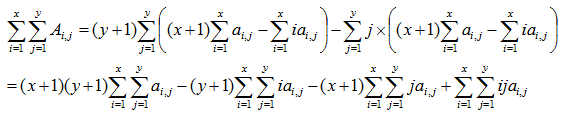
由上面公式看出,只需要维护下面四个元素的矩阵和,就可以求出
所以,用二维树状数组维护上面四个矩阵和就行了。
此时a[i][j]+=t,代表b[i][j],b[i+1][j],...,b[n][j]都增加了t,
也就代表
A[i][j],A[i][j+1],...A[i][n]都增加了t
A[i+1][j],A[i+1][j+1],...A[i+1][n]都增加了t
...
A[n][j],A[n][j+1],...A[n][n]都增加了t
于是矩形区域的加法也就不难表示了,调用4次Add(点修改)就行了。
矩形区域的求和也不难表示了,调用4次Sum就行了。
void AddSquare(int x1,int y1,int x2,int y2,int K){Add(x1,y1,K);Add(x2+1,y2+1,K);Add(x1,y2+1,-K);Add(x2+1,y1,-K);
}
long long SumSquare(int x1,int y1,int x2,int y2){return Sum(x2,y2)-Sum(x1-1,y2)-Sum(x2,y1-1)+Sum(x1-1,y1-1);
}
时间复杂度:
暴力法做矩形修改的话,时间复杂度是
二维树状数组的时间复杂度:
数组元素个数为1000*1000的时候,Sum操作平均用到24.38个数组元素,
Add操作平均用到25.60个数组元素。
由于本题维护了4个数组,所以每个Sum平均涉及97.52个元素。
所以每个Add平均涉及102.40个元素。
然后每次操作用到了4次Add或者4次Sum.
所以二维树状数组每次操作平均更改400个数组元素的值。
同等情况下,暴力法需要更改的元素个数最少为1,最多为10^6.在1000*1000,随机数据的情况下暴力法平均每次操作更改62500元素,极限数据下更改1000000元素
随机数据下用时是二维树状数组的156倍,极限数据下是2500倍。
1000*1000时,10000个对整个数组的操作时(极限数据),减去输入输出的时间之后:
二维树状数组的用时:0.013s,暴力法用时:39.517s 约为3000倍。
1000*1000,随机进行100000次操作时,减去输入输出时间后:
二维树状数组用时:0.314s 暴力法用时:47.27s. 约为150.54倍。
实验跟计算基本符合。
最后附上代码:
#define LL long long
int n,m;
LL A[1027][1027][4];
LL C[4];
void Add(int x,int y,LL K){//点修改C[0]=K;C[1]=K*y;C[2]=K*x;C[3]=K*x*y;int xx=x;while(xx <= n){int yy=y; while(yy <= n){A[xx][yy][0]+=C[0];A[xx][yy][1]+=C[1];A[xx][yy][2]+=C[2];A[xx][yy][3]+=C[3];yy+=yy&-yy; }xx+=xx&-xx;}
}
LL Sum(int x,int y){//1..x,1..y的区域求和C[0]=C[1]=C[2]=C[3]=0; int xx=x;while(xx > 0){int yy=y;while(yy > 0){C[0]+=A[xx][yy][0];C[1]+=A[xx][yy][1];C[2]+=A[xx][yy][2];C[3]+=A[xx][yy][3];yy-=yy&-yy;}xx-=xx&-xx;}return (x+1)*(y+1)*C[0]-(x+1)*C[1]-(y+1)*C[2]+C[3];
}
void AddSquare(int x1,int y1,int x2,int y2,int K){//矩形区域的修改Add(x1,y1,K);Add(x2+1,y2+1,K);Add(x1,y2+1,-K);Add(x2+1,y1,-K);
}
LL SumSquare(int x1,int y1,int x2,int y2){//矩形区域的求和return Sum(x2,y2)-Sum(x1-1,y2)-Sum(x2,y1-1)+Sum(x1-1,y1-1);
}这篇关于树状数组实现矩阵中矩形区域的修改以及求和的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!