06-图3 六度空间（C）

本文主要是介绍06-图3 六度空间（C），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

这个很好想，尤其是经过图的连通集，所以这一次我才有之前写的代码为主体以邻接表的方法构建了方法一，至于运用 邻接矩阵，可以查看我之前的图的连通集这一方案，稍微改装，便解决这一问题了。

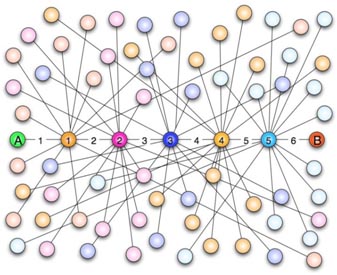
“六度空间”理论又称作“六度分隔（Six Degrees of Separation）”理论。这个理论可以通俗地阐述为：“你和任何一个陌生人之间所间隔的人不会超过六个，也就是说，最多通过五个人你就能够认识任何一个陌生人。”如图1所示。

图1 六度空间示意图

“六度空间”理论虽然得到广泛的认同，并且正在得到越来越多的应用。但是数十年来，试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因，这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具，能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。

假如给你一个社交网络图，请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。

输入格式:

输入第1行给出两个正整数，分别表示社交网络图的结点数N（1<N≤103，表示人数）、边数M（≤33×N，表示社交关系数）。随后的M行对应M条边，每行给出一对正整数，分别是该条边直接连通的两个结点的编号（节点从1到N编号）。

输出格式:

对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比，精确到小数点后2位。每个结节点输出一行，格式为“结点编号:（空格）百分比%”。

输入样例:

10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10

输出样例:

1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%

 我的AC:

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>typedef struct ENode *PtrToENode;
typedef PtrToENode Edge;
struct ENode{int V1, V2;int Weight;
};typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{int V;int Weight;PtrToAdjVNode Next;
};typedef struct VNode **AdjList;
struct VNode{PtrToAdjVNode FirstEdge;
};typedef struct GNode *PtrToGNode;
typedef PtrToGNode LGraph;
struct GNode{int Nv;int Ne;AdjList G;
};typedef struct Node *QNode;
struct Node{int Data;QNode Next;
};
typedef struct QNode *Queue;
struct QNode{QNode front;QNode rear;
};LGraph Build_Graph();
LGraph Init_Graph(int Nv, int Ne);
void Insert_Graph(LGraph M, Edge E);
void Sort_Graph(PtrToAdjVNode *Link);
void Visit(int Vertex);
int BFS(LGraph M, int Vertex,  bool *Visited);
void SDS(LGraph M);
Queue Init_Q();
void Add_Q(Queue Q, int Vertex);
int Delete_Q(Queue Q);
bool IsEmpty_Q(Queue Q);int main()
{LGraph M;M = Build_Graph();SDS(M);return 0;
}
LGraph Build_Graph()
{LGraph M;Edge E;int Nv, Ne;int i;scanf("%d%d", &Nv, &Ne);M = Init_Graph(Nv, Ne);E = (Edge)malloc(sizeof(struct ENode));if(M ->Nv){for(i = 1; i <= (M ->Ne); i++){scanf("%d%d", &E ->V1, &E ->V2);Insert_Graph(M, E);}}return M;
}
LGraph Init_Graph(int Nv, int Ne)
{LGraph M;M = (LGraph)malloc(sizeof(struct GNode));M ->Nv = Nv;M ->Ne = Ne;M ->G = (AdjList)malloc(sizeof(struct VNode) * Nv);for(int i = 0; i <= Nv; i++){M ->G[i] = (struct VNode*)malloc(sizeof(struct VNode));M ->G[i] ->FirstEdge = NULL;}return M;
}
void Insert_Graph(LGraph M, Edge E)
{// 无向图PtrToAdjVNode NewNode1, NewNode2;NewNode1 = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode1 ->V = E ->V2;NewNode1 ->Weight = E ->Weight;NewNode1 ->Next = M ->G[E ->V1] ->FirstEdge;M ->G[E ->V1] ->FirstEdge = NewNode1;Sort_Graph(&(M ->G[E ->V1] ->FirstEdge));NewNode2 = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));NewNode2 ->V = E ->V1;NewNode2 ->Weight = E ->Weight;NewNode2 ->Next = M ->G[E ->V2] ->FirstEdge;M ->G[E ->V2] ->FirstEdge = NewNode2;Sort_Graph(&(M ->G[E ->V2] ->FirstEdge));
}
void Sort_Graph(PtrToAdjVNode *Link)
{PtrToAdjVNode head, Temp, Key;head = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));head ->Next = (*Link) ->Next;Temp = head;Key = (*Link);Key ->Next = NULL;if(!(head ->Next)){return ;}while(head ->Next){if(Key ->V > (head ->Next ->V)){head = head ->Next;}else{Key ->Next = head ->Next;head ->Next = Key;break;}}if(!(head ->Next)){head ->Next = Key;}(*Link) = Temp ->Next;return ;
}int BFS(LGraph M, int Vertex,  bool *Visited)
{Queue Q;PtrToAdjVNode G;int V;int count = 1, level = 0, last = Vertex, tail;Q = Init_Q();Visited[Vertex] = true;Add_Q(Q, Vertex);while(!IsEmpty_Q(Q)){V = Delete_Q(Q);for(G = M ->G[V] ->FirstEdge; G; G = G ->Next){if(Visited[G ->V] == false){Visited[G ->V] = true;Add_Q(Q, G ->V);count++;tail = G ->V;}}if(V == last){level++;last = tail;}if(level == 6){break;}}return count;
}
Queue Init_Q()
{Queue Q;Q = (Queue)malloc(sizeof(struct QNode));Q ->front = NULL;Q ->rear = Q ->front;return Q;
}
void Add_Q(Queue Q, int Vertex)
{QNode Node;Node = (QNode)malloc(sizeof(struct Node));Node ->Data = Vertex;Node ->Next = NULL;if(!(Q ->front) && !(Q ->rear)){Q ->front = Node;Q ->rear = Node;}else{Q ->rear ->Next = Node;Q ->rear = Node;}
}
int Delete_Q(Queue Q)
{if(IsEmpty_Q(Q)){printf("很遗憾，是空的！\n");return -1;}else{QNode Temp;int Vertex;if(Q ->front == Q ->rear){Vertex = Q ->front ->Data;Q ->front = NULL;Q ->rear = NULL;}else{Temp = Q ->front;Q ->front = Q ->front ->Next;Vertex = Temp ->Data;free(Temp);}return Vertex;}
}
bool IsEmpty_Q(Queue Q)
{return Q ->front == NULL;
}
void SDS(LGraph M)
{bool *Visited;int count;Visited = (bool*)calloc(M ->Nv + 1, sizeof(bool));for(int V = 1; V <= M->Nv;V++) {count = BFS(M, V, Visited);printf("%d: %.2f%%\n", V, ((count * 100.0) / (M ->Nv)));for(int V = 1; V <= M->Nv;V++){Visited[V] = false;}}free(Visited);
}

这篇关于06-图3 六度空间（C）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---