本文主要是介绍Java五子棋之坐标校正,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上篇针对了Java项目中的解构思维,在这篇内容中我们不妨从整体项目中拆解拿出一个非常重要的五子棋逻辑实现:坐标校正,我们如何使漫无目的鼠标点击变得有序化和可控化呢?
目录
一、从鼠标监听到获取坐标
1.MouseListener和MouseAdapter
2.mousePressed方法
二、坐标校正的具体实现方法
1.关于fillOval方法
2.坐标获取
3.坐标转换
4.坐标还原
一、从鼠标监听到获取坐标
1.MouseListener和MouseAdapter
一共有五种鼠标事件:Clicked(点击)、Pressed(按下)、Released(释放)、Exited(鼠标位置离开界面)、Entered(鼠标位置进入界面)
public interface MouseListener extends EventListener {/*** Invoked when the mouse button has been clicked (pressed* and released) on a component.* @param e the event to be processed*/public void mouseClicked(MouseEvent e);/*** Invoked when a mouse button has been pressed on a component.* @param e the event to be processed*/public void mousePressed(MouseEvent e);/*** Invoked when a mouse button has been released on a component.* @param e the event to be processed*/public void mouseReleased(MouseEvent e);/*** Invoked when the mouse enters a component.* @param e the event to be processed*/public void mouseEntered(MouseEvent e);/*** Invoked when the mouse exits a component.* @param e the event to be processed*/public void mouseExited(MouseEvent e);
}
总的来说MouseAdapter用起来要比MouseListener要更方便一点,因为当我们用 MouseListener 时,必须实现接口中的所有方法,即使可能只对其中的一部分感兴趣,如果不全部列出就会出现报错。而MouseAdapter帮助我们简化处理了鼠标事件,我们只需要选择性使用并重写。
证明如下:
需要注意的是MouseListener是一个接口,应该使用implements而不是extends


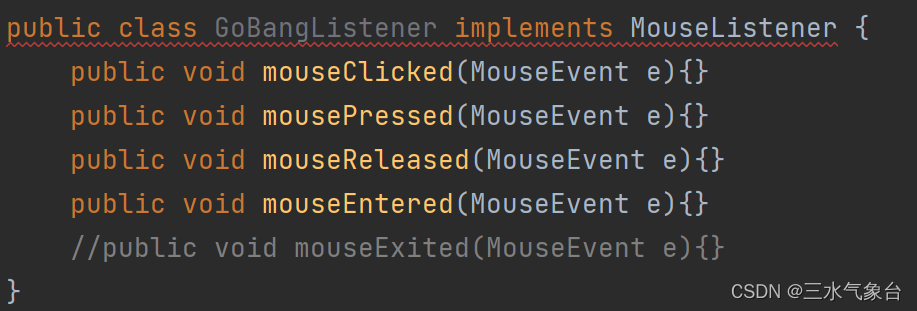
2.mousePressed方法
我们下棋是通过鼠标点击屏幕实现的,所以我们需要重写mousePressed方法,在其中实现一些具体的方法逻辑。
二、坐标校正的具体实现方法
1.关于fillOval方法
g.fillOval(x,y,w,h);这是一个有坑的方法,正常我们认为画圆认为点击的地方即为圆心,但fillOval方法的x,y是所画圆的左上角坐标,即实际圆心坐标还要各偏离点击的size/2
g.fillOval(x-size/2,y-size/2,w,h);2.坐标获取
int x1 = e.getX();
int y1 = e.getY();
System.out.println("点击的x坐标:"+x1+"点击的y坐标:"+y1);3.坐标转换
将点击的大坐标(x1,y1)转换为棋盘上的某行某列小坐标(r,c)
棋盘的范围是:(x0-size/2,y0-size/2)~ (x0+size*row+size/2,y0+size*col+size/2)
int r0 = (x1+SIZE/2-x0)/SIZE;int c0 = (y1+SIZE/2-y0)/SIZE;重点:之所以要加上size/2是防止点击(x0-size/2,y0-size/2)的位置时候出现负数,可以自行验算一下
4.坐标还原
还原出来的坐标就应该可以达到我们正常落子的要求了。
int wzqX = x0- SIZE/2 + r0*SIZE;
int wzqY = y0- SIZE/2 + c0*SIZE;
g.fillOval(wzqX,wzqY,SIZE,SIZE);这里要减去size/2就是因为第一点里fillOval我们所说的小细节的地方。
以上就是本次五子棋小游戏中坐标获取与校对的全部内容啦。
这篇关于Java五子棋之坐标校正的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





