线性回归（Linear Regression）原理详解及Python代码示例

本文主要是介绍线性回归（Linear Regression）原理详解及Python代码示例，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、线性回归原理详解

线性回归是一种基本的统计方法，用于预测因变量（目标变量）与一个或多个自变量（特征变量）之间的线性关系。线性回归模型通过拟合一条直线（在多变量情况下是一条超平面）来最小化预测值与真实值之间的误差。

1. 线性回归模型

对于单变量线性回归，模型的表达式为：

其中：

y是目标变量。
x是特征变量。
β0是截距项（偏置）。
β1是特征变量的系数。

对于多变量线性回归，模型的表达式为：

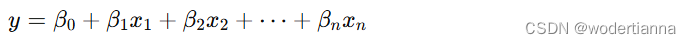
其中：

y是目标变量。
x1,x2,…,xn是多个特征变量。
β0是截距项（偏置）。
β1,β2,…,βn是各特征变量的系数。

2. 最小二乘法（Ordinary Least Squares, OLS）

线性回归通过最小二乘法来估计模型参数，即最小化所有预测误差的平方和。对于给定的训练数据集 (xi,yi)，目标是找到使得误差平方和最小的 β值。

误差平方和（损失函数）的公式为：

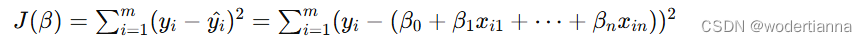
其中 m是样本数量，yi^ 是第 i个样本的预测值，通过最小化这个损失函数，可以得到最优的模型参数 β。

二、Python代码示例

下面是使用Python实现线性回归的代码示例。我们将使用scikit-learn库来构建和训练线性回归模型，并预测一些数据。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score# 生成示例数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建线性回归模型并进行训练
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)# 进行预测
y_pred = lin_reg.predict(X_test)# 打印模型参数
print("截距（Intercept）:", lin_reg.intercept_)
print("系数（Coefficients）:", lin_reg.coef_)# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("均方误差（MSE）:", mse)
print("决定系数（R^2）:", r2)# 绘制回归直线
plt.scatter(X_test, y_test, color='blue', label='Actual')
plt.plot(X_test, y_pred, color='red', linewidth=2, label='Predicted')
plt.xlabel('Feature')
plt.ylabel('Target')
plt.title('Linear Regression')
plt.legend()
plt.show()

代码解释：