本文主要是介绍Android自定义系列——8.Path之贝塞尔曲线，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
贝塞尔曲线能干什么
贝塞尔曲线作用十分广泛，简单举几个的栗子:
QQ小红点拖拽效果
一些炫酷的下拉刷新控件
阅读软件的翻书效果
一些平滑的折线图的制作
很多炫酷的动画效果
理解贝塞尔曲线的原理
一阶曲线原理：
一阶曲线是没有控制点的，仅有两个数据点(A 和 B)，最终动态过程如下：
(本文中贝塞尔曲线相关的动态演示图片来自维基百科)。一阶曲线其实就是前面讲解过的lineTo。
二阶曲线原理：
二阶曲线由两个数据点(A 和 C)，一个控制点(B)来描述曲线状态，大致如下：
连接AB BC，并在AB上取点D，BC上取点E，使其满足条件：
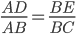
连接DE，取点F，使得:
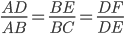
这样获取到的点F就是贝塞尔曲线上的一个点，动态过程如下：
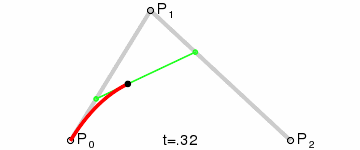二阶曲线对应的方法是quadTo。
三阶曲线原理：
三阶曲线由两个数据点(A 和 D)，两个控制点(B 和 C)来描述曲线状态，如下：
三阶曲线计算过程与二阶类似，具体可以见下图动态效果：
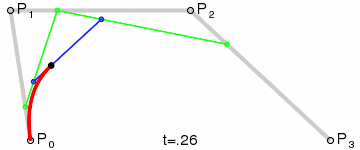三阶曲线对应的方法是cubicTo。
了解贝塞尔曲线相关函数使用方法
一阶曲线：
一阶曲线是一条线段，可以参见上一篇Android自定义系列——7.Path之基本操作 。
二阶曲线：
二阶曲线是由两个数据点，一个控制点构成。
上图中绘制出了辅助点和辅助线，从上面的动态图可以看出，贝塞尔曲线在动态变化过程中有类似于橡皮筋一样的弹性效果，因此在制作一些弹性效果的时候很常用。
public class Bezier extends View {private Paint mPaint;private int centerX, centerY;private PointF start, end, control;public Bessel1(Context context) {super(context);mPaint = new Paint();mPaint.setColor(Color.BLACK);mPaint.setStrokeWidth(8);mPaint.setStyle(Paint.Style.STROKE);mPaint.setTextSize(60);start = new PointF(0,0);end = new PointF(0,0);control = new PointF(0,0);}@Overrideprotected void onSizeChanged(int w, int h, int oldw, int oldh) {super.onSizeChanged(w, h, oldw, oldh);centerX = w/2;centerY = h/2;// 初始化数据点和控制点的位置start.x = centerX-200;start.y = centerY;end.x = centerX+200;end.y = centerY;control.x = centerX;control.y = centerY-100;}@Overridepublic boolean onTouchEvent(MotionEvent event) {// 根据触摸位置更新控制点，并提示重绘control.x = event.getX();control.y = event.getY();invalidate();return true;}@Overrideprotected void onDraw(Canvas canvas) {super.onDraw(canvas);// 绘制数据点和控制点mPaint.setColor(Color.GRAY);mPaint.setStrokeWidth(20);canvas.drawPoint(start.x,start.y,mPaint);canvas.drawPoint(end.x,end.y,mPaint);canvas.drawPoint(control.x,control.y,mPaint);// 绘制辅助线mPaint.setStrokeWidth(4);canvas.drawLine(start.x,start.y,control.x,control.y,mPaint);canvas.drawLine(end.x,end.y,control.x,control.y,mPaint);// 绘制贝塞尔曲线mPaint.setColor(Color.RED);mPaint.setStrokeWidth(8);Path path = new Path();path.moveTo(start.x,start.y);path.quadTo(control.x,control.y,end.x,end.y);canvas.drawPath(path, mPaint);}
}三阶曲线：
三阶曲线由两个数据点和两个控制点来控制曲线状态。
public class Bezier2 extends View {private Paint mPaint;private int centerX, centerY;private PointF start, end, control1, control2;private boolean mode = true;public Bezier2(Context context) {this(context, null);}public Bezier2(Context context, AttributeSet attrs) {super(context, attrs);mPaint = new Paint();mPaint.setColor(Color.BLACK);mPaint.setStrokeWidth(8);mPaint.setStyle(Paint.Style.STROKE);mPaint.setTextSize(60);start = new PointF(0, 0);end = new PointF(0, 0);control1 = new PointF(0, 0);control2 = new PointF(0, 0);}public void setMode(boolean mode) {this.mode = mode;}@Overrideprotected void onSizeChanged(int w, int h, int oldw, int oldh) {super.onSizeChanged(w, h, oldw, oldh);centerX = w / 2;centerY = h / 2;// 初始化数据点和控制点的位置start.x = centerX - 200;start.y = centerY;end.x = centerX + 200;end.y = centerY;control1.x = centerX;control1.y = centerY - 100;control2.x = centerX;control2.y = centerY - 100;}@Overridepublic boolean onTouchEvent(MotionEvent event) {// 根据触摸位置更新控制点，并提示重绘if (mode) {control1.x = event.getX();control1.y = event.getY();} else {control2.x = event.getX();control2.y = event.getY();}invalidate();return true;}@Overrideprotected void onDraw(Canvas canvas) {super.onDraw(canvas);//drawCoordinateSystem(canvas);// 绘制数据点和控制点mPaint.setColor(Color.GRAY);mPaint.setStrokeWidth(20);canvas.drawPoint(start.x, start.y, mPaint);canvas.drawPoint(end.x, end.y, mPaint);canvas.drawPoint(control1.x, control1.y, mPaint);canvas.drawPoint(control2.x, control2.y, mPaint);// 绘制辅助线mPaint.setStrokeWidth(4);canvas.drawLine(start.x, start.y, control1.x, control1.y, mPaint);canvas.drawLine(control1.x, control1.y,control2.x, control2.y, mPaint);canvas.drawLine(control2.x, control2.y,end.x, end.y, mPaint);// 绘制贝塞尔曲线mPaint.setColor(Color.RED);mPaint.setStrokeWidth(8);Path path = new Path();path.moveTo(start.x, start.y);path.cubicTo(control1.x, control1.y, control2.x,control2.y, end.x, end.y);canvas.drawPath(path, mPaint);}
}三阶曲线相比于二阶曲线可以制作更加复杂的形状，但是对于高阶的曲线，用低阶的曲线组合也可达到相同的效果，就是传说中的降阶。因此我们对贝塞尔曲线的封装方法一般最高只到三阶曲线。
贝塞尔曲线使用实例
首先要明确一个内容，就是在什么情况下需要使用贝塞尔曲线？可能会有如下几个方面：
| 序号 | 内容 | 用例 |
|---|---|---|
| 1 | 事先不知道曲线状态，需要实时计算时 | 天气预报气温变化的平滑折线图 |
| 2 | 显示状态会根据用户操作改变时 | QQ小红点，仿真翻书效果 |
| 3 | 一些比较复杂的运动状态(配合PathMeasure使用) | 复杂运动状态的动画效果 |
贝塞尔曲线的主要优点是可以实时控制曲线状态，并可以通过改变控制点的状态实时让曲线进行平滑的状态变化。
思路分析：
我们最终的需要的效果是将一个圆转变成一个心形，通过分析可知，圆可以由四段三阶贝塞尔曲线组合而成，如下：
心形也可以由四段的三阶的贝塞尔曲线组成，如下：
两者的差别仅仅在于数据点和控制点位置不同，因此只需要调整数据点和控制点的位置，就能将圆形变为心形。
核心难点：
1.如何得到数据点和控制点的位置？
关于使用绘制圆形的数据点与控制点早就已经有人详细的计算好了，可以参考https://stackoverflow.com/questions/1734745/how-to-create-circle-with-b%C3%A9zier-curves
而对于心形的数据点和控制点，可以由圆形的部分数据点和控制点平移后得到
2.如何达到渐变效果？
渐变其实就是每次对数据点和控制点稍微移动一点，然后重绘界面，在短时间多次的调整数据点与控制点，使其逐渐接近目标值，通过不断的重绘界面达到一种渐变的效果。
`public class Bezier3 extends View {
private static final float C = 0.551915024494f; // 一个常量，用来计算绘制圆形贝塞尔曲线控制点的位置
private Paint mPaint;
private int mCenterX, mCenterY;private PointF mCenter = new PointF(0,0);
private float mCircleRadius = 200; // 圆的半径
private float mDifference = mCircleRadius*C; // 圆形的控制点与数据点的差值private float[] mData = new float[8]; // 顺时针记录绘制圆形的四个数据点
private float[] mCtrl = new float[16]; // 顺时针记录绘制圆形的八个控制点private float mDuration = 1000; // 变化总时长
private float mCurrent = 0; // 当前已进行时长
private float mCount = 100; // 将时长总共划分多少份
private float mPiece = mDuration/mCount; // 每一份的时长public Bezier3(Context context) {this(context, null);}public Bezier3(Context context, AttributeSet attrs) {super(context, attrs);mPaint = new Paint();mPaint.setColor(Color.BLACK);mPaint.setStrokeWidth(8);mPaint.setStyle(Paint.Style.STROKE);mPaint.setTextSize(60);// 初始化数据点mData[0] = 0;mData[1] = mCircleRadius;mData[2] = mCircleRadius;mData[3] = 0;mData[4] = 0;mData[5] = -mCircleRadius;mData[6] = -mCircleRadius;mData[7] = 0;// 初始化控制点mCtrl[0] = mData[0]+mDifference;mCtrl[1] = mData[1];mCtrl[2] = mData[2];mCtrl[3] = mData[3]+mDifference;mCtrl[4] = mData[2];mCtrl[5] = mData[3]-mDifference;mCtrl[6] = mData[4]+mDifference;mCtrl[7] = mData[5];mCtrl[8] = mData[4]-mDifference;mCtrl[9] = mData[5];mCtrl[10] = mData[6];mCtrl[11] = mData[7]-mDifference;mCtrl[12] = mData[6];mCtrl[13] = mData[7]+mDifference;mCtrl[14] = mData[0]-mDifference;mCtrl[15] = mData[1];
}@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {super.onSizeChanged(w, h, oldw, oldh);mCenterX = w / 2;mCenterY = h / 2;
}@Override
protected void onDraw(Canvas canvas) {super.onDraw(canvas);drawCoordinateSystem(canvas); // 绘制坐标系canvas.translate(mCenterX, mCenterY); // 将坐标系移动到画布中央canvas.scale(1,-1); // 翻转Y轴drawAuxiliaryLine(canvas);// 绘制贝塞尔曲线mPaint.setColor(Color.RED);mPaint.setStrokeWidth(8);Path path = new Path();path.moveTo(mData[0],mData[1]);path.cubicTo(mCtrl[0], mCtrl[1], mCtrl[2], mCtrl[3], mData[2], mData[3]);path.cubicTo(mCtrl[4], mCtrl[5], mCtrl[6], mCtrl[7], mData[4], mData[5]);path.cubicTo(mCtrl[8], mCtrl[9], mCtrl[10], mCtrl[11], mData[6], mData[7]);path.cubicTo(mCtrl[12], mCtrl[13], mCtrl[14], mCtrl[15], mData[0], mData[1]);canvas.drawPath(path, mPaint);mCurrent += mPiece;if (mCurrent < mDuration){mData[1] -= 120/mCount;mCtrl[7] += 80/mCount;mCtrl[9] += 80/mCount;mCtrl[4] -= 20/mCount;mCtrl[10] += 20/mCount;postInvalidateDelayed((long) mPiece);}
}// 绘制辅助线
private void drawAuxiliaryLine(Canvas canvas) {// 绘制数据点和控制点mPaint.setColor(Color.GRAY);mPaint.setStrokeWidth(20);for (int i=0; i<8; i+=2){canvas.drawPoint(mData[i],mData[i+1], mPaint);}for (int i=0; i<16; i+=2){canvas.drawPoint(mCtrl[i], mCtrl[i+1], mPaint);}// 绘制辅助线mPaint.setStrokeWidth(4);for (int i=2, j=2; i<8; i+=2, j+=4){canvas.drawLine(mData[i],mData[i+1],mCtrl[j],mCtrl[j+1],mPaint);canvas.drawLine(mData[i],mData[i+1],mCtrl[j+2],mCtrl[j+3],mPaint);}canvas.drawLine(mData[0],mData[1],mCtrl[0],mCtrl[1],mPaint);canvas.drawLine(mData[0],mData[1],mCtrl[14],mCtrl[15],mPaint);
}// 绘制坐标系
private void drawCoordinateSystem(Canvas canvas) {canvas.save(); // 绘制做坐标系canvas.translate(mCenterX, mCenterY); // 将坐标系移动到画布中央canvas.scale(1,-1); // 翻转Y轴Paint fuzhuPaint = new Paint();fuzhuPaint.setColor(Color.RED);fuzhuPaint.setStrokeWidth(5);fuzhuPaint.setStyle(Paint.Style.STROKE);canvas.drawLine(0, -2000, 0, 2000, fuzhuPaint);canvas.drawLine(-2000, 0, 2000, 0, fuzhuPaint);canvas.restore();
}
}
`
这篇关于Android自定义系列——8.Path之贝塞尔曲线的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
