本文主要是介绍JupyterLab使用指南(七):JupyterLab使用 LaTeX 生成数学公式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在 JupyterLab 中,可以使用 LaTeX 语法生成复杂的数学公式。JupyterLab 内置对 LaTeX 的支持,使得我们可以方便地在 notebook 中编写和展示数学公式。以下是详细的步骤和示例。
1. 使用 LaTeX 生成数学公式
LaTeX 是一种专门用于排版数学公式的语言。JupyterLab 支持在 Markdown 单元格和代码单元格中使用 LaTeX。
1.1 在 Markdown 单元格中使用 LaTeX
在 Markdown 单元格中,使用美元符号 $ 包围 LaTeX 表达式可以生成行内公式,使用双美元符号 $$ 包围 LaTeX 表达式可以生成块级公式。
行内公式
这是一个行内公式:$E = mc^2$
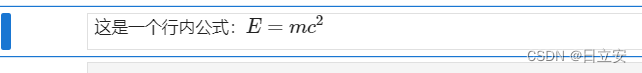
块级公式
这是一个块级公式:
$$
E = mc^2
$$

1.2 在代码单元格中使用 LaTeX
在代码单元格中,可以使用 IPython.display 模块的 Math 类来显示 LaTeX 公式。
from IPython.display import display, Math# 显示 LaTeX 公式
display(Math(r'E = mc^2'))

2. 复杂数学公式示例
下面是一些复杂数学公式的示例,展示了如何在 JupyterLab 中使用 LaTeX 编写和显示它们。
2.1 二次方程的求解公式
二次方程的求解公式为:
$$
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
$$

2.2 积分公式
一个常见的积分公式:
$$
\int_{a}^{b} f(x) \, dx = F(b) - F(a)
$$

2.3 微分方程
一阶线性微分方程的通解:
$$
y' + p(x)y = q(x)
$$
其通解为:
$$
y = e^{-\int p(x) \, dx} \left( \int q(x)e^{\int p(x) \, dx} \, dx + C \right)
$$

2.4 矩阵表示
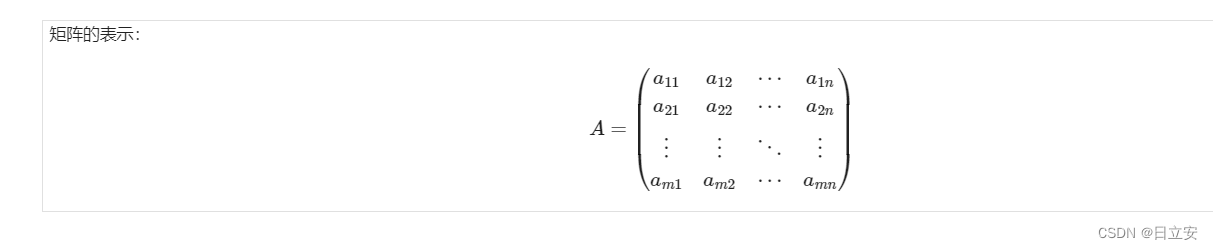
矩阵的表示:
$$
A = \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix}
$$
2.5 复杂的多行公式
复杂的多行公式:
$$
\begin{align}
a & = b + c \\& = d + e + f
\end{align}
$$

3. 使用 SymPy 生成 LaTeX 公式
SymPy 是一个用于符号计算的 Python 库,可以与 LaTeX 结合使用,在 JupyterLab 中生成复杂的数学公式。
3.1 安装 SymPy
首先,确保已安装 SymPy:
pip install sympy
3.2 使用 SymPy 生成 LaTeX 公式
以下是使用 SymPy 生成和显示 LaTeX 公式的示例:
import sympy as sp
from IPython.display import display, Math# 定义符号
x, y = sp.symbols('x y')# 定义一个表达式
expr = sp.sin(x) + sp.cos(y)# 将表达式转换为 LaTeX 公式
latex_expr = sp.latex(expr)# 显示 LaTeX 公式
display(Math(latex_expr))

在这个示例中,我们定义了一个符号表达式 expr,然后使用 sp.latex 函数将其转换为 LaTeX 公式,最后使用 display 和 Math 类在 JupyterLab 中显示公式。
在 JupyterLab 中使用 LaTeX 生成复杂数学公式不仅方便,而且可以通过与 SymPy 等符号计算库结合,实现动态的公式生成和显示。这对于数据科学家、研究人员和教育工作者来说是一个非常强大的功能,能够显著提升数学表达和计算的效率。通过掌握这些工具和技术,可以使你的 Jupyter notebook 不仅仅是一个代码和数据的展示平台,更是一个强大的交互式文档和计算环境。
这篇关于JupyterLab使用指南(七):JupyterLab使用 LaTeX 生成数学公式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






