本文主要是介绍深度学习 --- stanford cs231学习笔记四(训练神经网络的几个重要组成部分之一,激活函数),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
训练神经网络的几个重要组成部分 一
1,激活函数(activation functions)
激活函数是神经网络之于线性分类器的最大进步,最大贡献,即,引入了非线性。这些非线性函数可以被分成两大类,饱和非线性函数和不饱和非线性函数。
1,1 饱和非线性函数
1,1,1 Sigmoid
原函数:
函数的导数:

sigmoid函数的性质:
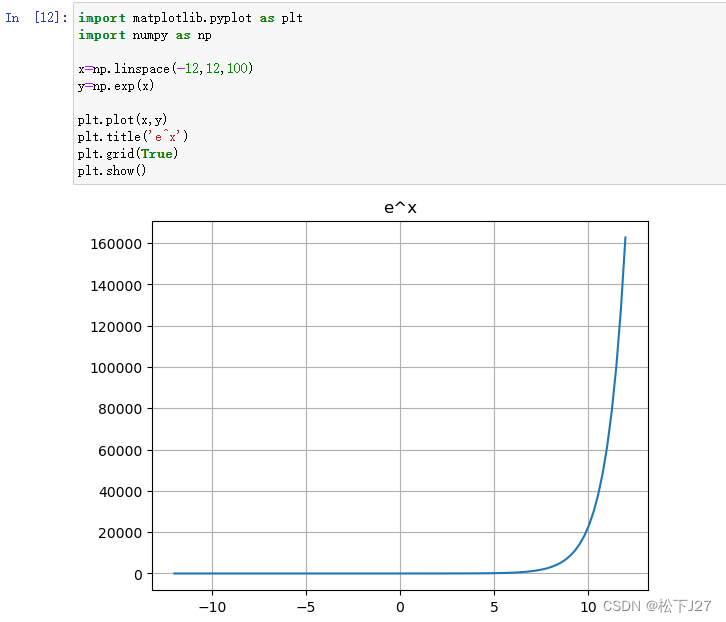
结合指数函数的图像可知,当x<0时,-x>0,指数函数随着x的减小而增大,当x=-10时,几乎exp(-(-10))=exp(10),约等于2W2,如果x再继续小下去sigmoid的分母就变成无穷大了,此时sigmoid趋近于0。即,当x<0时,随着x越来越小,sigmoid函数越来越趋近于0。
反之,当x>0时,-x<0,指数函数随着x的增大而减小,当x=10时,几乎exp(-(10))=exp(-10),约等于0,如果x再增加下去sigmoid的分母就变成1了,此时sigmoid趋近于1/1=1。即,当x>0时,随着x越来越大,sigmoid函数越来越趋近于1。
函数值始终为正,且不关于0对称。
sigmoid函数的缺点:梯度消失
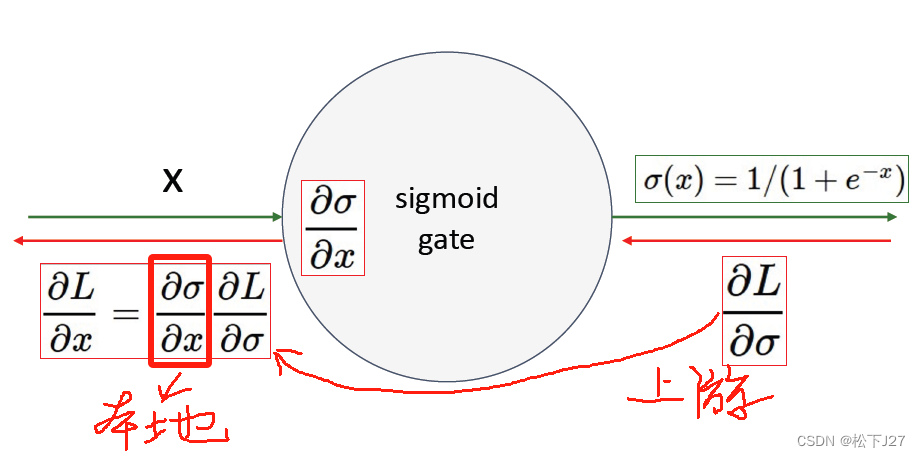
在计算损失函数L关于x的梯度时,不论上游梯度传过来的是什么,sigmoid函数的本地梯度为:
因此,当x过大时,sigmoid的值为1,1-sigmoid为0,则,本地梯度为0。当x过小时,sigmoid的值为0,同样会导致本地梯度为0。如此一来,损失函数L就无法通过梯度下降法去更新W。

当然sigmoid函数还有其他问题,例如,均值不为0,和输出总是正数,这会导致梯度下降时的zig-zag问题,也就是梯度下降速度慢的问题。但相对于梯度消失这个最为严重的问题,可忽略不计。
1,1,2 Tanh(x)双曲正切函数
双曲正切函数有点像是sigmoid函数经过整体向下平移后得到的函数。
原函数:
函数的导数:


函数的特点:
函数的值域为-1~1,输出有正有负,均值为0,即函数值关于0对称。从一定程度上弥补了sigmoid函数的不足。
函数的缺点:梯度消失
已知双曲正切的函数为:
他所对应的导数为:
该导数作为本地梯度,当x较大时,tanh(x)=1,平方后仍然为1,上面的导数为1-1=0。
当x较小时,tanh(x)=-1,平方后为1,导数为0。
这也就是说,双曲正切函数仍然会有梯度消失的问题,也就是梯度为0的问题。
饱和非线性函数的小结:
饱和非线性函数在神经网络中指的是那些在输入值非常大或非常小时,其输出值趋于某个常数值的激活函数,也就是说他不能很好的保持x的原貌。常见函数有sigmoid和tanh。
1,2 不饱和非线性函数
1,2,1 ReLU激活函数(Rectified Linear Unit)
原函数:
函数的导数:

ReLU函数的特性:
1,不同于sigmoid和tanh,对于大于0的输入,在前向传播的过程中ReLU会使得输出等于输入,而不是把任何输入都限制在一个比较狭窄的值域内。
2,计算速度非常快,只需对输入x做一个判断。
3,学习效率高,迭代速度快。
函数的问题:
结合该函数的梯度来看,当x<0时,会出现本地梯度为0。如此一来,无论上游梯度传过来的是什么,最终结果都是0,使得梯度无法更新。也就说,ReLU函数依然存在梯度消失的问题。

值得一提的是ReLU函数在著名的AlexNet中被首次提出,这也可以说是这篇paper最重要的贡献之一。ReLU的出现使得训练时的迭代速度比tanh快了接近6倍。
1,2,2 Leaky ReLU
为了克服ReLU函数中,当x为负值时,梯度直接为0的情况,leaky ReLU使得x为负数时,依然会保留一个较小的梯度,这个值很小但不为0。
原函数:
函数的导数:

函数的特性:
1. x > 0时:Leaky ReLU的输出等于输入,导数为1。
2. x <= 0时:输出是输入乘以一个小于一的系数,导数为该系数。使得x为负时,避免了梯度为0的情况,依然可以跟新W。
函数存在的问题:
虽然有非零梯度,但负值区间的梯度较小,导致该区间的权重更新速度较慢。
1,2,3 ELU
ELU函数是ReLU函数更进一步的改进版。
原函数:
函数的导数:

函数的特性:
1. x > 0时:与Leaky ReLU相同。
2. x <= 0时:导数恒为正,同样避免了梯度为0的情况,可以跟新W。
1,2,4 SELU

1,2,5 GELU

1,3 summary of activation functions
在上面关于不饱和激活函数的介绍我到后面就懒得写了,主要原有是因为下面这个PPt中的结论。这个作者在三个著名的网络中,分别使用了不同的不饱和激活函数并比较了准确率。可见,ReLU函数在这三组实验中的表现并不俗,和表现最好的其他激活函数比也就相差了不到1%的准确率。但ReLU函数的计算确是最简单了,计算速度最快的。做到这里还得是人家AlexNet的作者Alex牛,ReLU函数就在在这篇文章中被首次提及并成功运用的。他的出现几乎彻底取代了原有的sigmoid函数和tanh函数。

结合上面所说的,cs231n给出了如下建议:
1,在选择activation function时,不要太过纠结,直接无脑的使用ReLU就好,只是要明白为什么。
2,如果你想追求更好效果,即,更高准确率,可是试试其他激活函数。但不要用sigmoid和tanh。
3,在一些非常非常新的模型中可能会用到GeLU。

(全文完)
--- 作者,松下J27
参考文献(鸣谢):
1,Stanford University CS231n: Deep Learning for Computer Vision
2,训练神经网络(第一部分)_哔哩哔哩_bilibili
3,10 Training Neural Networks I_哔哩哔哩_bilibili
4,Schedule | EECS 498-007 / 598-005: Deep Learning for Computer Vision
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27
这篇关于深度学习 --- stanford cs231学习笔记四(训练神经网络的几个重要组成部分之一,激活函数)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




