DP：完全背包+多重背包问题

2024-06-21 12:12
文章标签 问题 dp 背包 完全 多重

本文主要是介绍DP：完全背包+多重背包问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

完全背包和01背包的区别就是：可以多次选

一、完全背包（模版）

【模板】完全背包_牛客题霸_牛客网

#include <iostream>
#include<string.h>
using namespace std;
const int N=1001;
int n,V,w[N],v[N],dp[N][N];
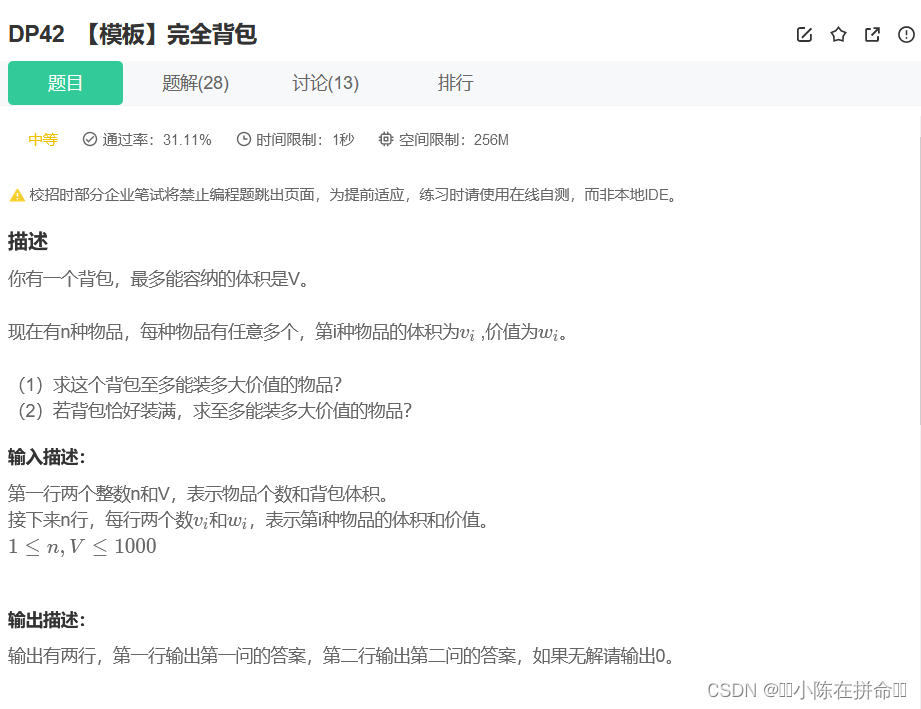
//dp[i][j]表示从前i个物品选，体积不超过j的最大价值
//dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i],dp[i-1][j-2v[i]]+2w[i]……)
//数学dp[i][j-v[i]]=max(dp[i-1][j-v[i]],dp[i-1][j-2v[i]]+w[i]……)
//dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]])
int main() 
{cin>>n>>V;for(int i=1;i<=n;++i) cin>>v[i]>>w[i];//解决第一问for(int i=1;i<=n;++i)for(int j=1;j<=V;++j){dp[i][j]=dp[i-1][j];if(j>=v[i]) dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);}  cout<<dp[n][V]<<endl;//解决第二问 //dp[i][j]表示从前i个物品选，体积正好为j的最大价值memset(dp,0,sizeof dp);//约定-1表示状态选不到 当i=0时 j>=1时  必然是没有状态的for(int j=1;j<=V;++j) dp[0][j]=-1;for(int i=1;i<=n;++i)for(int j=1;j<=V;++j){dp[i][j]=dp[i-1][j];if(j>=v[i]&&dp[i][j-v[i]]!=-1) dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);}  cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;return 0;
}

滚动数组的优化策略：

 区分：01背包的优化得是从右往左，而完全背包的优化得是从左往右

#include <iostream>
#include<string.h>
using namespace std;
const int N=1001;
int n,V,w[N],v[N],dp[N];
//dp[i][j]表示从前i个物品选，体积不超过j的最大价值
//dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i],dp[i-1][j-2v[i]]+2w[i]……)
//数学dp[i][j-v[i]]=max(dp[i-1][j-v[i]],dp[i-1][j-2v[i]]+w[i]……)
//dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]])
int main()  //优化必须要从左往右
{cin>>n>>V;for(int i=1;i<=n;++i) cin>>v[i]>>w[i];//解决第一问for(int i=1;i<=n;++i)for(int j=v[i];j<=V;++j)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);cout<<dp[V]<<endl;//解决第二问 //dp[i][j]表示从前i个物品选，体积正好为j的最大价值memset(dp,0,sizeof dp);//约定-1表示状态选不到 当i=0时 j>=1时  必然是没有状态的for(int j=1;j<=V;++j) dp[j]=-0x3f3f3f3f;for(int i=1;i<=n;++i)for(int j=v[i];j<=V;++j)dp[j]=max(dp[j],dp[j-v[i]]+w[i]);cout<<(dp[V]<0?0:dp[V])<<endl;return 0;
}

 二、零钱兑换

. - 力扣（LeetCode）

class Solution {
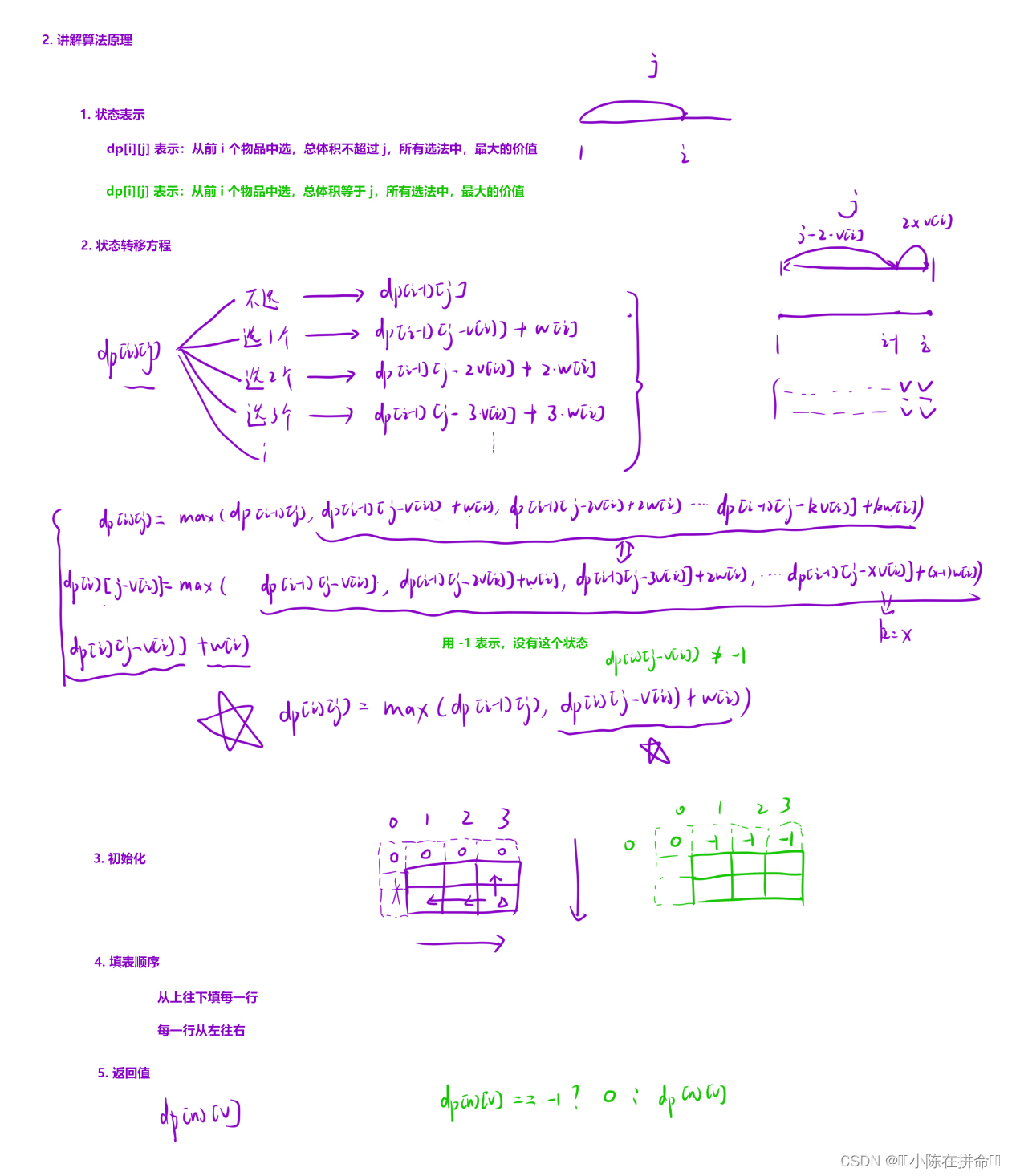
public:int coinChange(vector<int>& coins, int amount) {//dp[i][j]表示从前i个里面选 正好凑成j所需要的最少硬币个数//如果不选i dp[i-1][j]//选1个i   dp[i-1][j-coins[i-1]]+1//dp[i][j]=min(dp[i-1][j],dp[i-1][j-coins[i-1]]+1,dp[i-1][j-2coins[i-1]]+2……)//dp[i][j-coins[i-1]]=min(dp[i-1][j-coins[i-1]],dp[i-1][j-2coins[i-1]]+1……)//dp[i][j]=min(dp[i-1][j],dp[i][j-coins[i-1]]+1)const int INF=0x3f3f3f3f;int n=coins.size();vector<vector<int>> dp(n+1,vector<int>(amount+1));for(int j=1;j<=amount;++j) dp[0][j]=INF;for(int i=1;i<=n;++i)for(int j=1;j<=amount;++j){dp[i][j]=dp[i-1][j];if(j>=coins[i-1])  dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1);}return dp[n][amount]>=INF?-1:dp[n][amount];}
};

 滚动数组优化：

class Solution {
public:int coinChange(vector<int>& coins, int amount) {//dp[i][j]表示从前i个里面选 正好凑成j所需要的最少硬币个数//如果不选i dp[i-1][j]//选1个i   dp[i-1][j-coins[i-1]]+1//dp[i][j]=min(dp[i-1][j],dp[i-1][j-coins[i-1]]+1,dp[i-1][j-2coins[i-1]]+2……)//dp[i][j-coins[i-1]]=min(dp[i-1][j-coins[i-1]],dp[i-1][j-2coins[i-1]]+1……)//dp[i][j]=min(dp[i-1][j],dp[i][j-coins[i-1]]+1)const int INF=0x3f3f3f3f;int n=coins.size();vector<int> dp(amount+1,INF);dp[0]=0;for(int i=1;i<=n;++i)for(int j=coins[i-1];j<=amount;++j)dp[j]=min(dp[j],dp[j-coins[i-1]]+1);return dp[amount]>=INF?-1:dp[amount];}
};

三、零钱兑换II

. - 力扣（LeetCode）

class Solution {
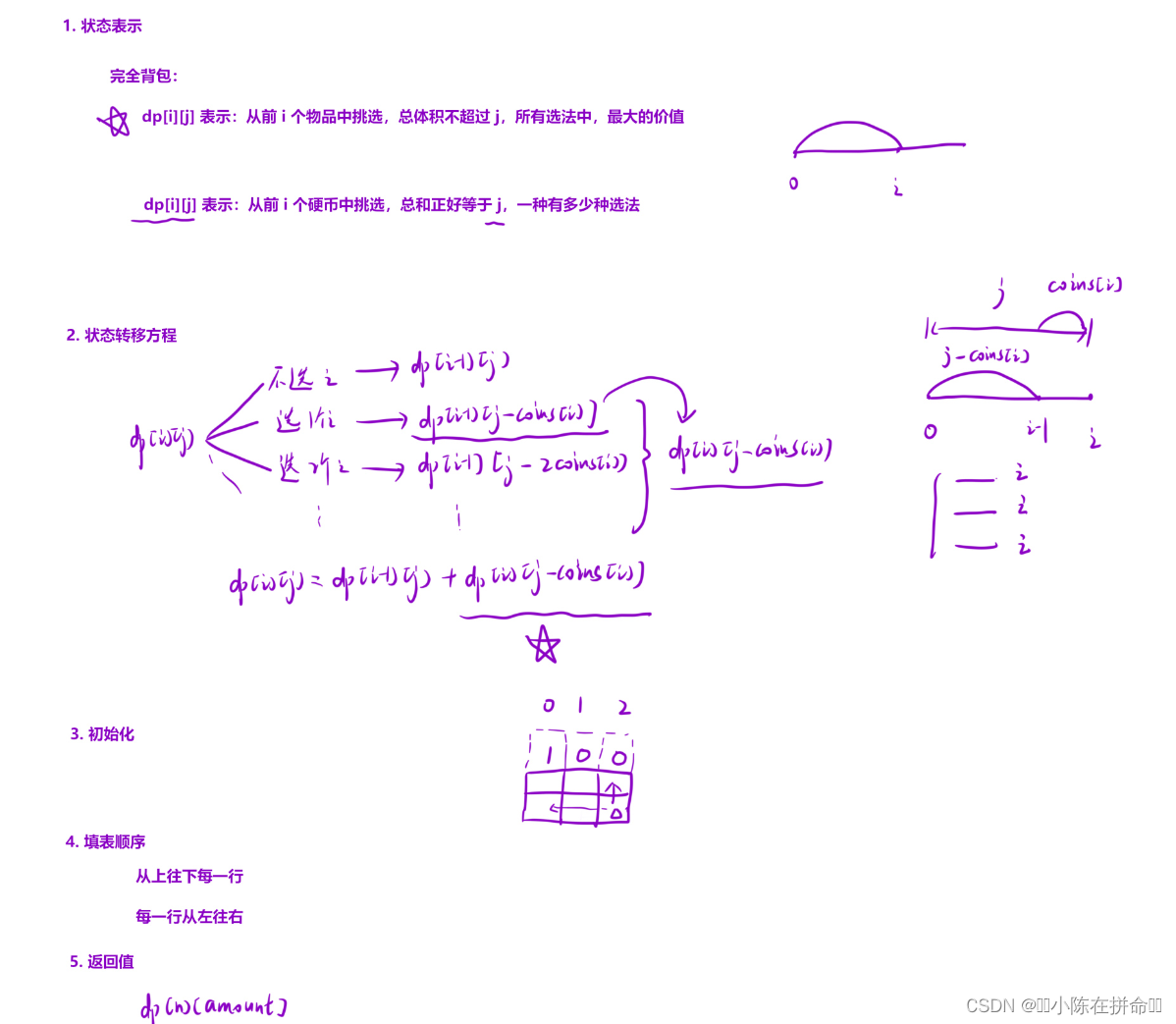
public:int change(int amount, vector<int>& coins) {//dp[i][j]表示从前i个硬币选，正好可以凑成总金额的硬币组合数//如果i不选 dp[i][j]+=dp[i-1][j]//如果i选1个 dp[i][j]+=dp[i-1][j-coins[i-1]]//dp[i][j]+=dp[i-1][j-coins[i-1]]+=dp[i-1][j-2coins[i-1]]……//dp[i][j]+=dp[i][j-coins[i-1]]int n=coins.size();//分析初始化 当j=0 都是一种选法  当i=0时 无论如何凑不出j 状态无效vector<vector<int>> dp(n+1,vector<int>(amount+1));dp[0][0]=1;for(int i=1;i<=n;++i)for(int j=0;j<=amount;++j) //不会越界，可以从0开始{dp[i][j]+=dp[i-1][j];if(j>=coins[i-1]) dp[i][j]+=dp[i][j-coins[i-1]];}return dp[n][amount];}
};

滚动数组做优化：

class Solution {
public:int change(int amount, vector<int>& coins) {//dp[i][j]表示从前i个硬币选，正好可以凑成总金额的硬币组合数//如果i不选 dp[i][j]+=dp[i-1][j]//如果i选1个 dp[i][j]+=dp[i-1][j-coins[i-1]]//dp[i][j]+=dp[i-1][j-coins[i-1]]+=dp[i-1][j-2coins[i-1]]……//dp[i][j]+=dp[i][j-coins[i-1]]int n=coins.size();//分析初始化 当j=0 都是一种选法  当i=0时 无论如何凑不出j 状态无效vector<int> dp(amount+1);dp[0]=1;for(int i=1;i<=n;++i)for(int j=coins[i-1];j<=amount;++j) //不会越界，可以从0开始dp[j]+=dp[j-coins[i-1]]; //+= 0不会影响填表return dp[amount];}
};

四、完全平方数

. - 力扣（LeetCode）

class Solution {
public:
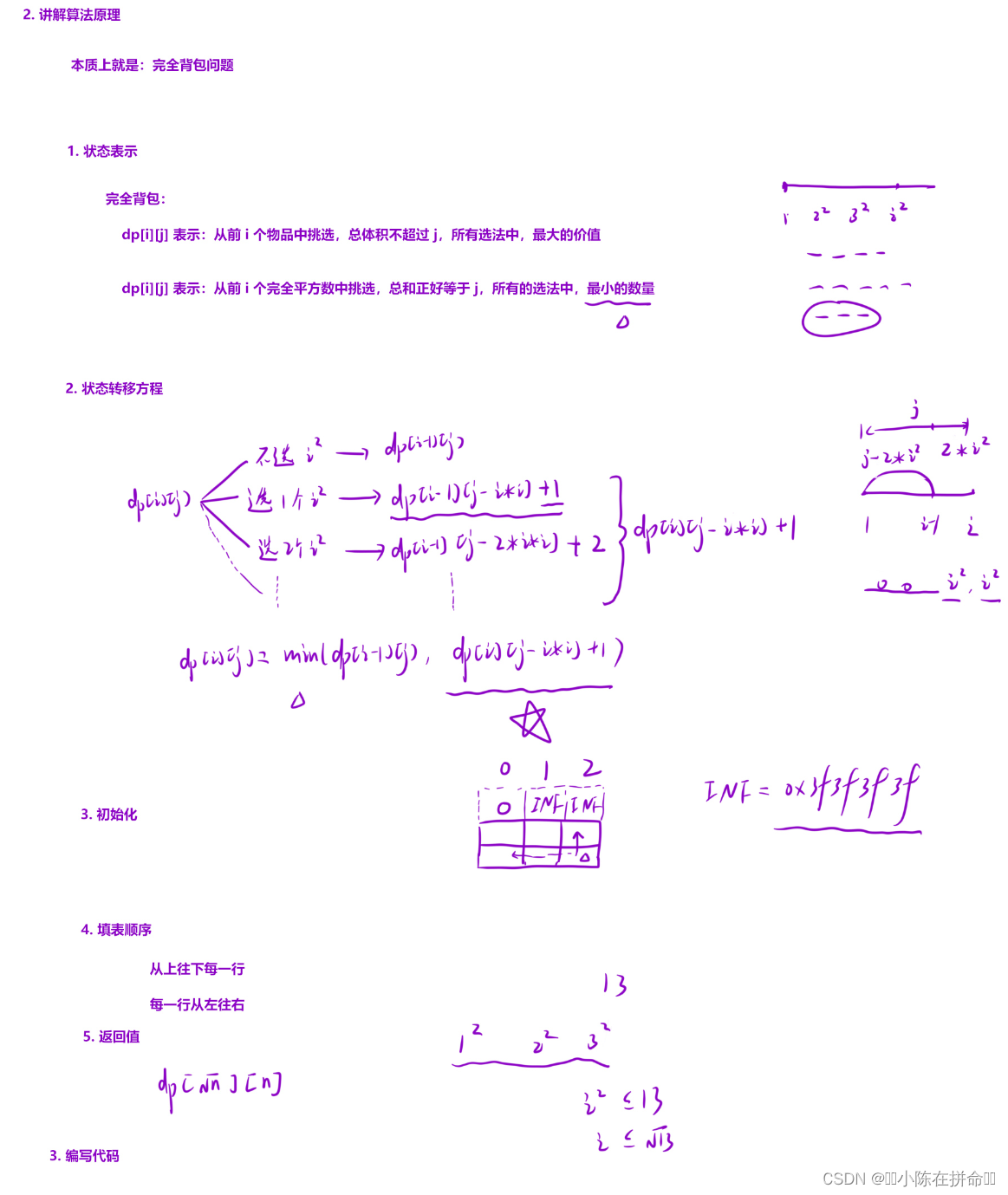
//不能用贪心策略 比如说1 4 9   组成12    444比9111好int numSquares(int n) {//1 4 9 16 25……//dp[i][j]表示从前i个数选，刚好为j的最少数量const int INF=0x3f3f3f3f;int m=sqrt(n);vector<int> dp(n+1,INF);//i=0的时候 不可能凑成j  j=0时 i取1dp[0]=0;for(int i=1;i<=m;++i)for(int j=i*i;j<=n;++j)dp[j]=min(dp[j],dp[j-i*i]+1);return dp[n]; //一定能选得到，因为1是平方数 所以必然能凑出来}
};

五、数位成本和为目标值的最大数字（经典dp还原）

. - 力扣（LeetCode）

class Solution {
public:string largestNumber(vector<int>& nums, int t) {//考虑数值长度问题，每个数字有相应成本，且长度均为1 //有若干物品，求给定费用下所能选择的最大价值  （完全背包）//得到的就是最大位数 然后从后往前想办法还原回来vector<int> dp(t+1,-0x3f3f3f3f);//会有不存在的状态//dp[i][j]表示前i个数选择 正好为j的最大选择数目dp[0]=1;for(int i=1;i<=9;++i)for(int j=nums[i-1];j<=t;++j)dp[j]=max(dp[j],dp[j-nums[i-1]]+1);//此时 dp[t]里存的就是选择的最大位数 然后要想办法进行还原if(dp[t]<0) return "0";string ret;//开始还原 从后往前还原for(int i=9;i>=1;--i){int u=nums[i-1];while(t>=u&&dp[t]==dp[t-u]+1)//说明选到这个数了{ret+=to_string(i);t-=u;}}return ret;}
};

六、获得分数的方法数（多重背包）

. - 力扣（LeetCode）

 该种类型题的具体分析请看第7题！！

class Solution {
public:const int MOD=1e9+7;int waysToReachTarget(int target, vector<vector<int>>& types) {//dp[i][j]表示从前i个数选 恰好分数为j的方案数 选择方式是types[1] //如果不选这个数 dp[i-1][j]//如果选 1个  dp[i-1][j-p[0]] //如果选2个  dp[i-1][j-2p[0]]int n=types.size();vector<vector<int>> dp(n+1,vector<int>(target+1));//初始化当i为0时 dp[0][0]=1;for(int i=1;i<=n;++i){int count=types[i-1][0],mark=types[i-1][1]; //count表示这道题的题数（选择次数）  mark表示这道题的分数for(int j=0;j<=target;++j){dp[i][j]=dp[i-1][j];for(int k=1;k<=count;++k){if(j>=k*mark) dp[i][j]=(dp[i][j]+dp[i-1][j-k*mark])%MOD;}}}return dp[n][target];}
};

滚动数组优化 

class Solution {
public:const int MOD=1e9+7;int waysToReachTarget(int target, vector<vector<int>>& types) {//dp[i][j]表示从前i个数选 恰好分数为j的方案数 选择方式是types[1] //如果不选这个数 dp[i-1][j]//如果选 1个  dp[i-1][j-p[0]] //如果选2个  dp[i-1][j-2p[0]]vector<int> dp(target+1);//初始化当i为0时 dp[0]=1;for(auto&p:types){int count=p[0],mark=p[1]; //count表示这道题的题数（选择次数）  mark表示这道题的分数       //会用到上一层的状态，所以滚动数组应该要从后往前for(int j=target;j>=0;--j){count=min(count,j/mark);for(int k=1;k<=count;++k)dp[j]=(dp[j]+dp[j-k*mark])%MOD;}}return dp[target];}
};

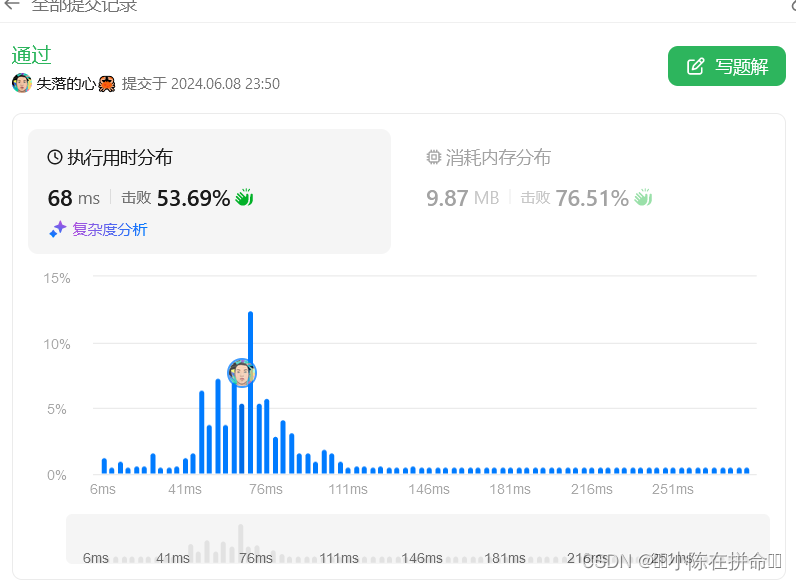
进阶优化：

class Solution {
public:const int MOD=1e9+7;int waysToReachTarget(int target, vector<vector<int>>& types) {//dp[i][j]表示从前i个数选 恰好分数为j的方案数 选择方式是types[1] //如果不选这个数 dp[i-1][j]//如果选 1个  dp[i-1][j-p[0]] //如果选2个  dp[i-1][j-2p[0]]//dp[i][j]+=dp[i-1][j-p[0]]……//dp[i][j-p[0]+=dp[i-1]][j-]vector<int> dp(target+1);//初始化当i为0时 dp[0]=1;for(auto&p:types){int count=p[0],mark=p[1]; //count表示这道题的题数（选择次数）  mark表示这道题的分数       //会用到上一层的状态，所以滚动数组应该要从后往前for(int j=mark;j<=target;++j)dp[j]=(dp[j]+dp[j-mark])%MOD;for(int j=target;j>=(count+1)*mark;--j)dp[j] = (dp[j] - dp[j - mark*(count + 1)] + MOD) % MOD; // 两个同余前缀和的差//防止搞出负数}return dp[target];}
};

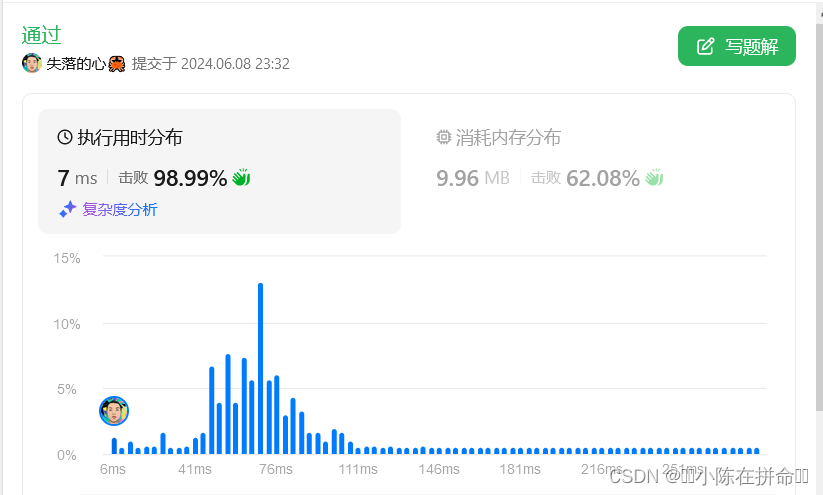
七、带和限制的子多重集合的数目（经典多重背包模版题）

. - 力扣（LeetCode）

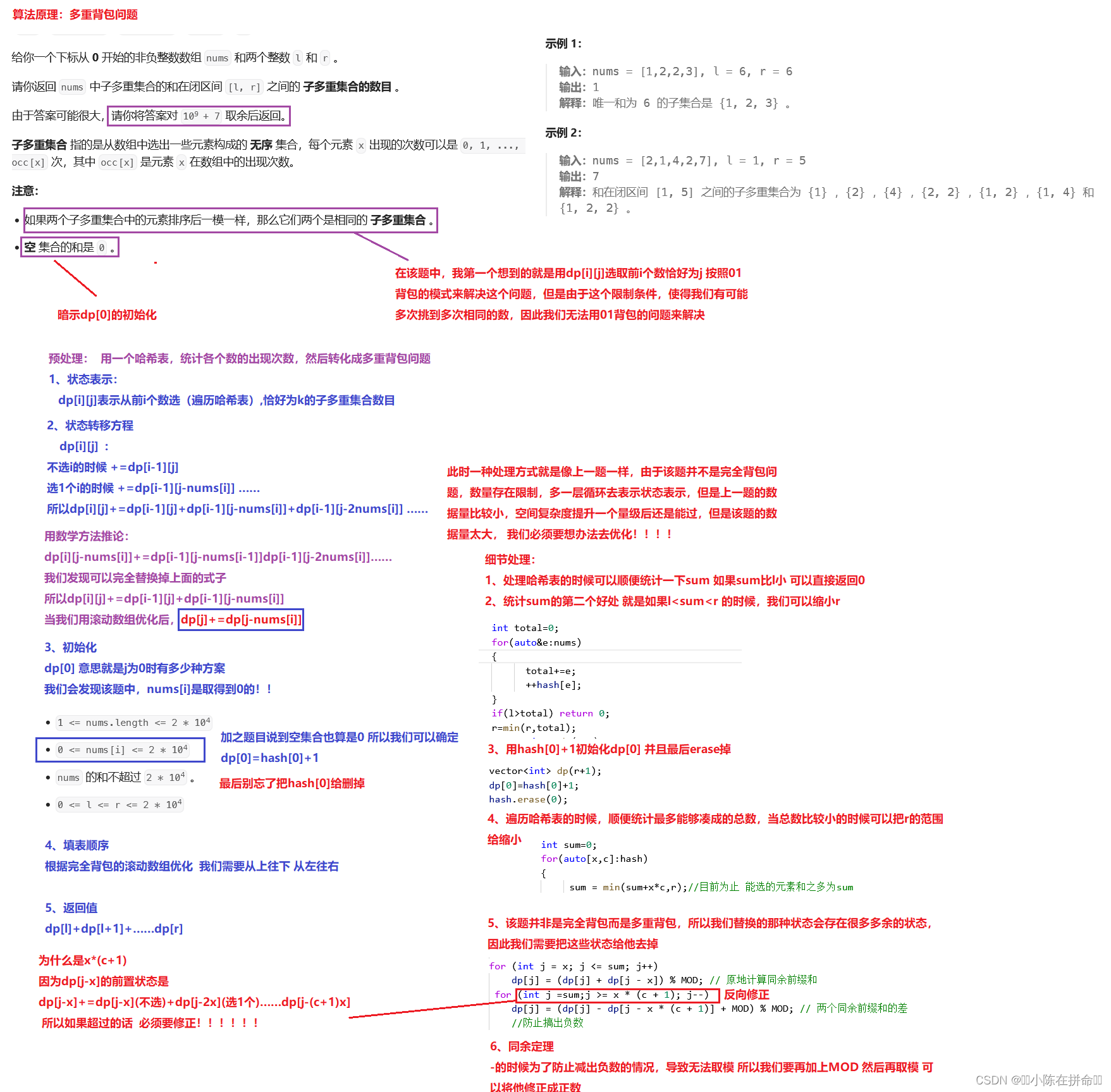
 直接做滚动数组优化：

class Solution {
public:const int MOD=1e9+7;int countSubMultisets(vector<int>& nums, int l, int r) {//01背包 每个数选或者不选 限制范围是l-r//dp[i][j]表示从前i个数选  凑成和恰好为j//但是需要一个哈希表来帮助我们知道每个数究竟可以选多少次unordered_map<int,int> hash;int total=0;for(auto&e:nums) {total+=e;++hash[e];}if(l>total) return 0;r=min(r,total);vector<int> dp(r+1);//初始化 i=0时 无数可选dp[0]=hash[0]+1;hash.erase(0);int t=0;for(auto[x,c]:hash) //x是数 c是他的限制次数for(int j=r;j>=x;--j){c=min(c,j/x);for(int k=1;k<=c;++k)    //费时间 想办法用新的状态dp[j]=(dp[j]+dp[j-k*x])%MOD; }int sum=0;for(int j=l;j<=r;++j)sum=(sum+dp[j])%MOD;return sum;}
};

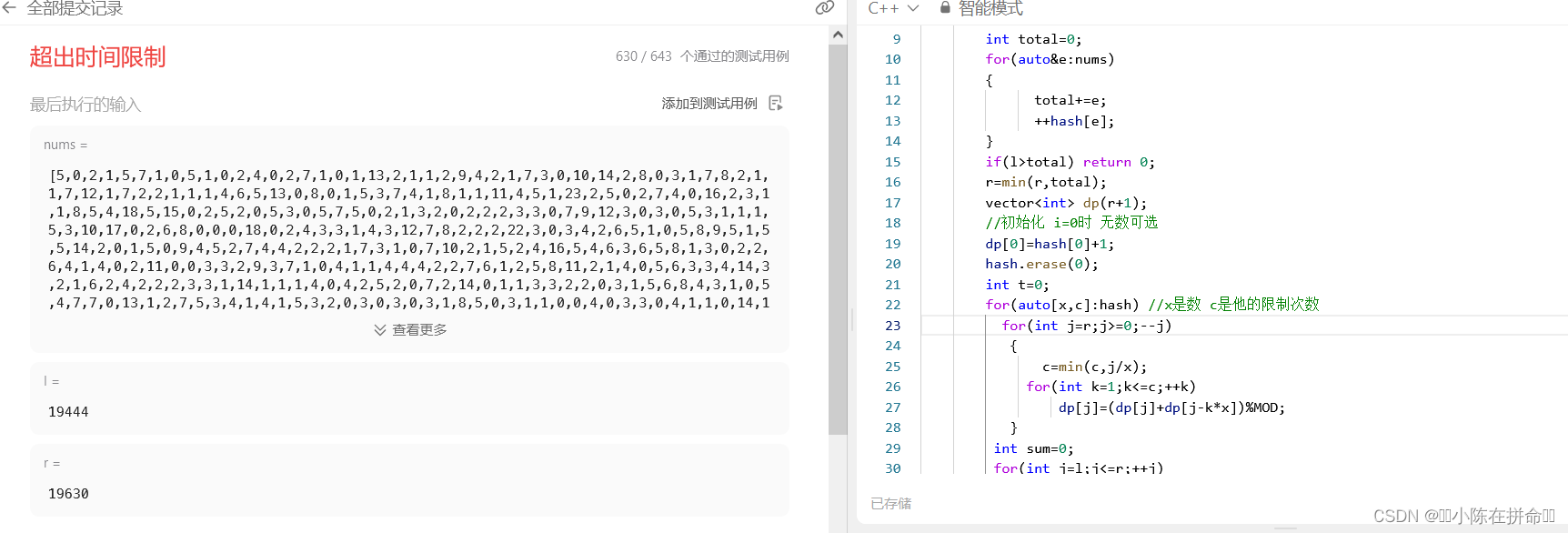
我们会发现由于数据量太大，用循环会超时，因此我们在这里不能用k那一层循环！！得换个方式

class Solution {
public:const int MOD=1e9+7;int countSubMultisets(vector<int>& nums, int l, int r) {//01背包 每个数选或者不选 限制范围是l-r//dp[i][j]表示从前i个数选  凑成和恰好为j//但是需要一个哈希表来帮助我们知道每个数究竟可以选多少次//类比完全背包的状态 dp[]unordered_map<int,int> hash;int total=0;for(auto&e:nums) {total+=e;++hash[e];}if(l>total) return 0;r=min(r,total);vector<int> dp(r+1);dp[0]=hash[0]+1;hash.erase(0);// dp[i][j]+=  dp[i-1][j-x]+dp[i-1][j-2*x]……// dp[i][j-x]+=dp[i-1][j-2x]+dp[i-1][j-3x]……int sum=0;for(auto[x,c]:hash){sum = min(sum+x*c,r);//目前为止 能选的元素和之多为sum for (int j = x; j <= sum; j++)dp[j] = (dp[j] + dp[j - x]) % MOD; // 原地计算同余前缀和for (int j =sum;j >= x * (c + 1); j--)dp[j] = (dp[j] - dp[j - x * (c + 1)] + MOD) % MOD; // 两个同余前缀和的差//防止搞出负数}int ret=0;for(int j=l;j<=r;++j)ret=(ret+dp[j])%MOD;return ret;}
};

 

这篇关于DP：完全背包+多重背包问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1081186。

相关文章

Kotlin Map映射转换问题小结

Kotlin Map映射转换问题小结

《KotlinMap映射转换问题小结》文章介绍了Kotlin集合转换的多种方法,包括map（一对一转换）、mapIndexed（带索引）、mapNotNull（过滤null）、mapKeys/map... 目录Kotlin 集合转换：map、mapIndexed、mapNotNull、mapKeys、map
阅读更多...
nginx中端口无权限的问题解决

nginx中端口无权限的问题解决

《nginx中端口无权限的问题解决》当Nginx日志报错bind()to80failed(13:Permissiondenied)时,这通常是由于权限不足导致Nginx无法绑定到80端口,下面就来... 目录一、问题原因分析二、解决方案1. 以 root 权限运行 Nginx（不推荐）2. 为 Nginx
阅读更多...
解决1093 - You can‘t specify target table报错问题及原因分析

解决1093 - You can‘t specify target table报错问题及原因分析

《解决1093-Youcan‘tspecifytargettable报错问题及原因分析》MySQL1093错误因UPDATE/DELETE语句的FROM子句直接引用目标表或嵌套子查询导致,... 目录报js错原因分析具体原因解决办法方法一：使用临时表方法二：使用JOIN方法三：使用EXISTS示例总结报错原
阅读更多...
Windows环境下解决Matplotlib中文字体显示问题的详细教程

Windows环境下解决Matplotlib中文字体显示问题的详细教程

《Windows环境下解决Matplotlib中文字体显示问题的详细教程》本文详细介绍了在Windows下解决Matplotlib中文显示问题的方法,包括安装字体、更新缓存、配置文件设置及编码調整,并... 目录引言问题分析解决方案详解1. 检查系统已安装字体2. 手动添加中文字体（以SimHei为例）步骤
阅读更多...
SpringSecurity整合redission序列化问题小结(最新整理)

SpringSecurity整合redission序列化问题小结(最新整理)

《SpringSecurity整合redission序列化问题小结(最新整理)》文章详解SpringSecurity整合Redisson时的序列化问题,指出需排除官方Jackson依赖,通过自定义反序... 目录1. 前言2. Redission配置2.1 RedissonProperties2.2 Red
阅读更多...
nginx 负载均衡配置及如何解决重复登录问题

nginx 负载均衡配置及如何解决重复登录问题

《nginx负载均衡配置及如何解决重复登录问题》文章详解Nginx源码安装与Docker部署,介绍四层/七层代理区别及负载均衡策略,通过ip_hash解决重复登录问题,对nginx负载均衡配置及如何... 目录一：源码安装：1.配置编译参数2.编译3.编译安装 二,四层代理和七层代理区别1.二者混合使用举例
阅读更多...
怎样通过分析GC日志来定位Java进程的内存问题

怎样通过分析GC日志来定位Java进程的内存问题

《怎样通过分析GC日志来定位Java进程的内存问题》：本文主要介绍怎样通过分析GC日志来定位Java进程的内存问题,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录一、GC 日志基础配置1. 启用详细 GC 日志2. 不同收集器的日志格式二、关键指标与分析维度1.
阅读更多...
Java 线程安全与 volatile与单例模式问题及解决方案

Java 线程安全与 volatile与单例模式问题及解决方案

《Java线程安全与volatile与单例模式问题及解决方案》文章主要讲解线程安全问题的五个成因（调度随机、变量修改、非原子操作、内存可见性、指令重排序）及解决方案,强调使用volatile关键字... 目录什么是线程安全线程安全问题的产生与解决方案线程的调度是随机的多个线程对同一个变量进行修改线程的修改操
阅读更多...
Redis出现中文乱码的问题及解决

Redis出现中文乱码的问题及解决

《Redis出现中文乱码的问题及解决》：本文主要介绍Redis出现中文乱码的问题及解决,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录1. 问题的产生2China编程. 问题的解决redihttp://www.chinasem.cns数据进制问题的解决中文乱码问题解决总结
阅读更多...
全面解析MySQL索引长度限制问题与解决方案

全面解析MySQL索引长度限制问题与解决方案

《全面解析MySQL索引长度限制问题与解决方案》MySQL对索引长度设限是为了保持高效的数据检索性能,这个限制不是MySQL的缺陷,而是数据库设计中的权衡结果,下面我们就来看看如何解决这一问题吧... 目录引言：为什么会有索引键长度问题？一、问题根源深度解析mysql索引长度限制原理实际场景示例二、五大解决
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2