【动态规划】路径问题 {二维动态规划；选择合适的状态表示方法；创建虚拟节点}

本文主要是介绍【动态规划】路径问题 {二维动态规划；选择合适的状态表示方法；创建虚拟节点}，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、经验总结

选择合适的状态表示方法
一般的，状态表示的方法有两种：

1. 以[i, j]位置为终点，正向填表；用之前的状态推导出dp[i][j]的值（从哪里来）；
2. 以[i, j]位置为起点，反向填表；用之后的状态推导出dp[i][j]的值（到哪里去）；

创建虚拟节点

• 一般虚拟节点设置在需要特殊处理的边界位置，在二维动态规划中，可以出现在矩阵的四边。
• 需要根据题目要求设置虚拟节点的初始值，以确保后续填表的正确性。
• 注意dp表与原始表的下标映射关系。

---

二、相关编程题

2.1 不同路径

题目链接

62. 不同路径 - 力扣（LeetCode）

题目描述

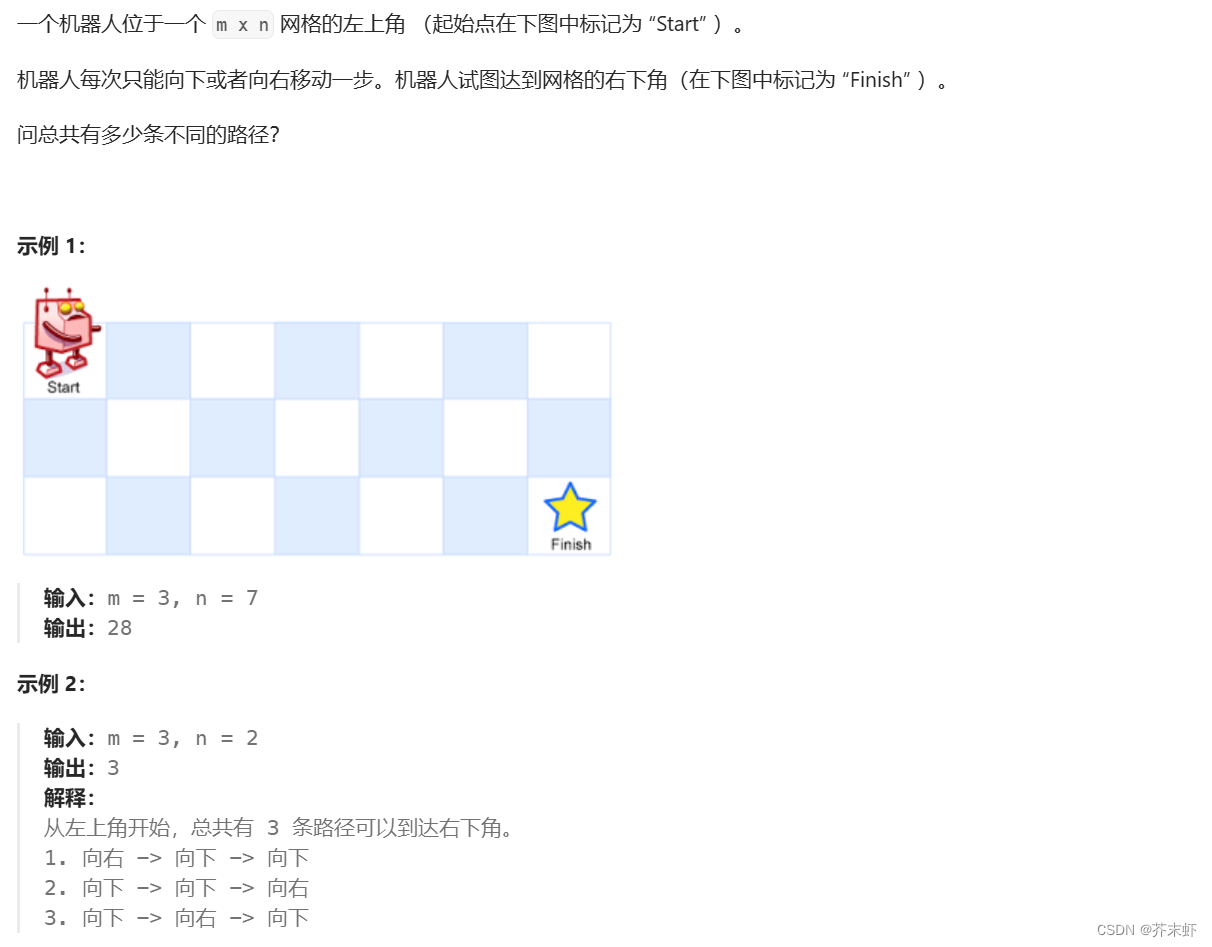
算法原理

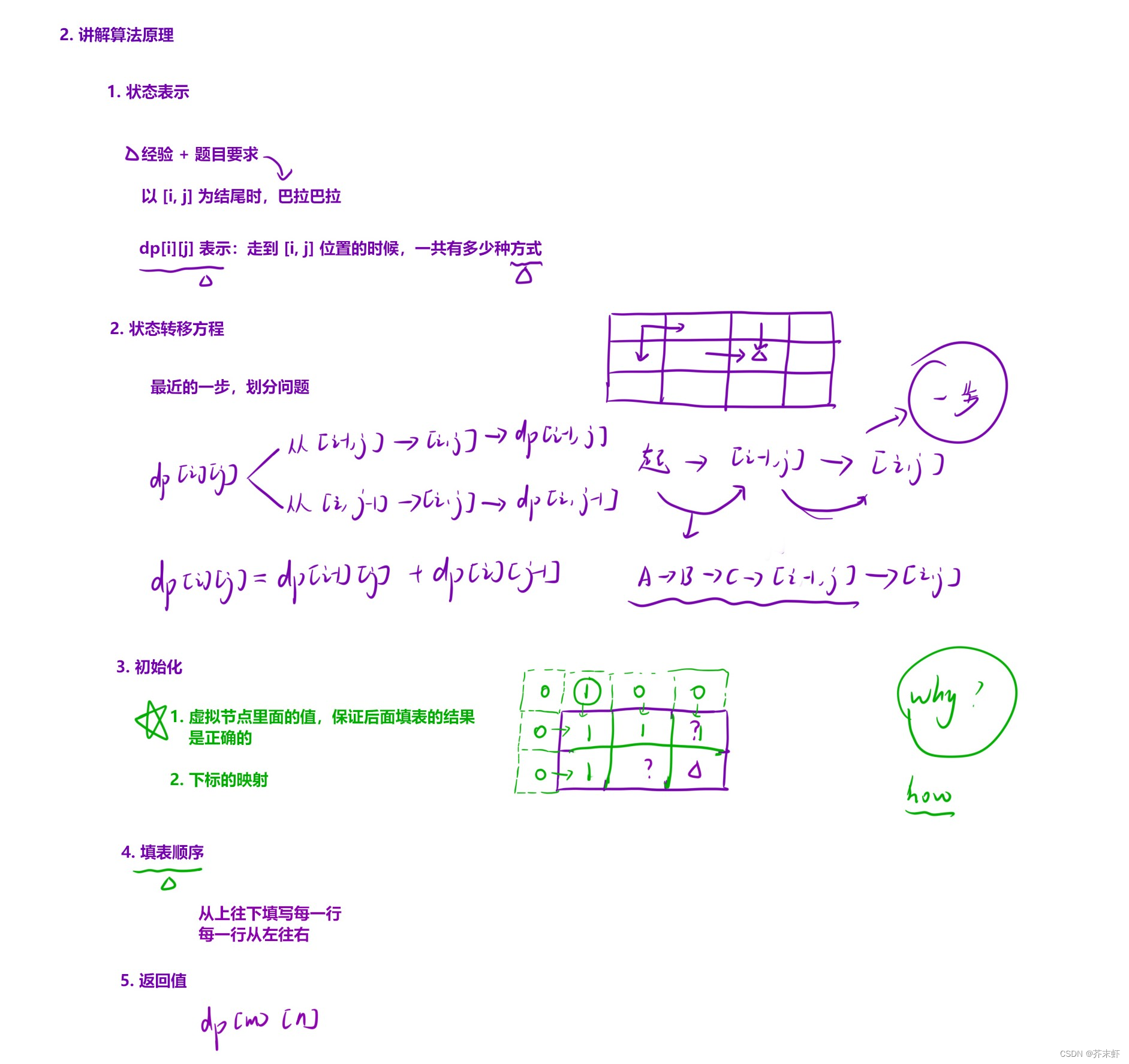
编写代码

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1, 0)); //多开一行一列作为虚拟节点dp[0][1] = 1; //虚拟节点的初始值，保证后续填表的正确性for(int i = 1; i <= m; ++i) //从上往下{for(int j = 1; j <= n; ++j) //从左往右{dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}
};

---

2.2 不同路径Ⅱ

题目链接

63. 不同路径 II - 力扣（LeetCode）

题目描述

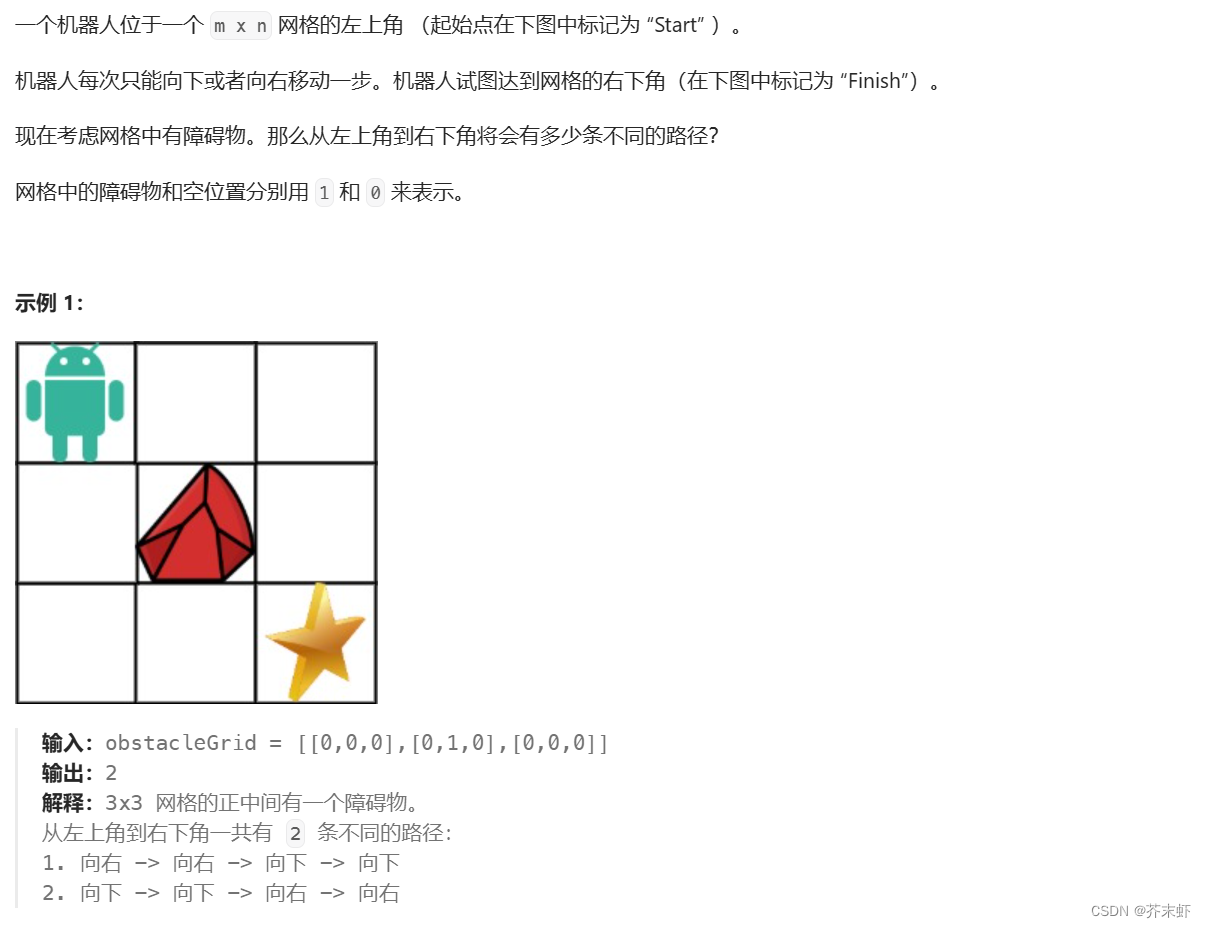
算法原理

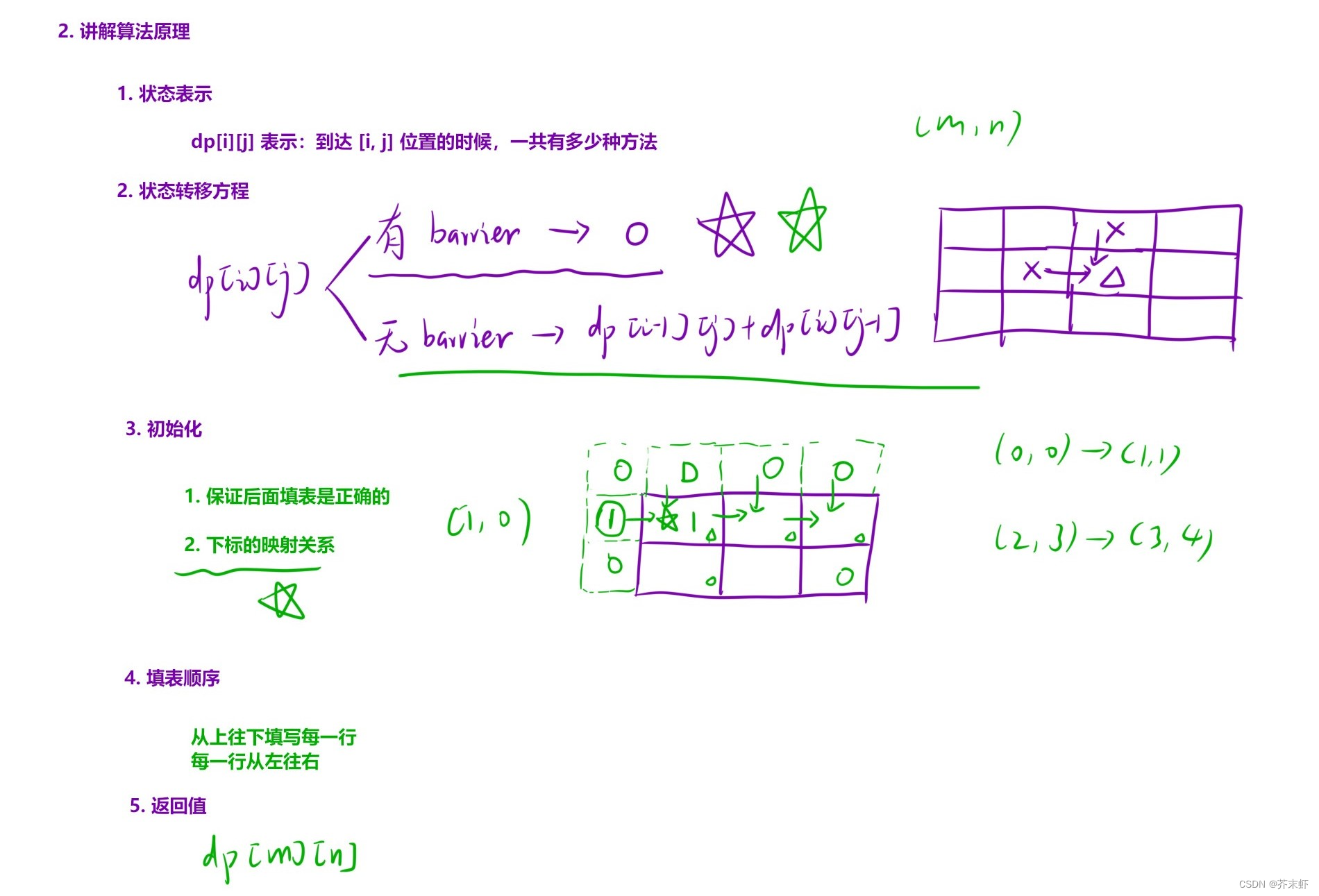
编写代码

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obs) {int m = obs.size(), n = obs[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1, 0));dp[0][1] = 1;for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){if(obs[i-1][j-1] == 1) continue; //注意dp表与原矩阵下标的映射关系dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}
};

---

2.3 珠宝的最高价值

题目链接

LCR 166. 珠宝的最高价值 - 力扣（LeetCode）

题目描述

算法原理

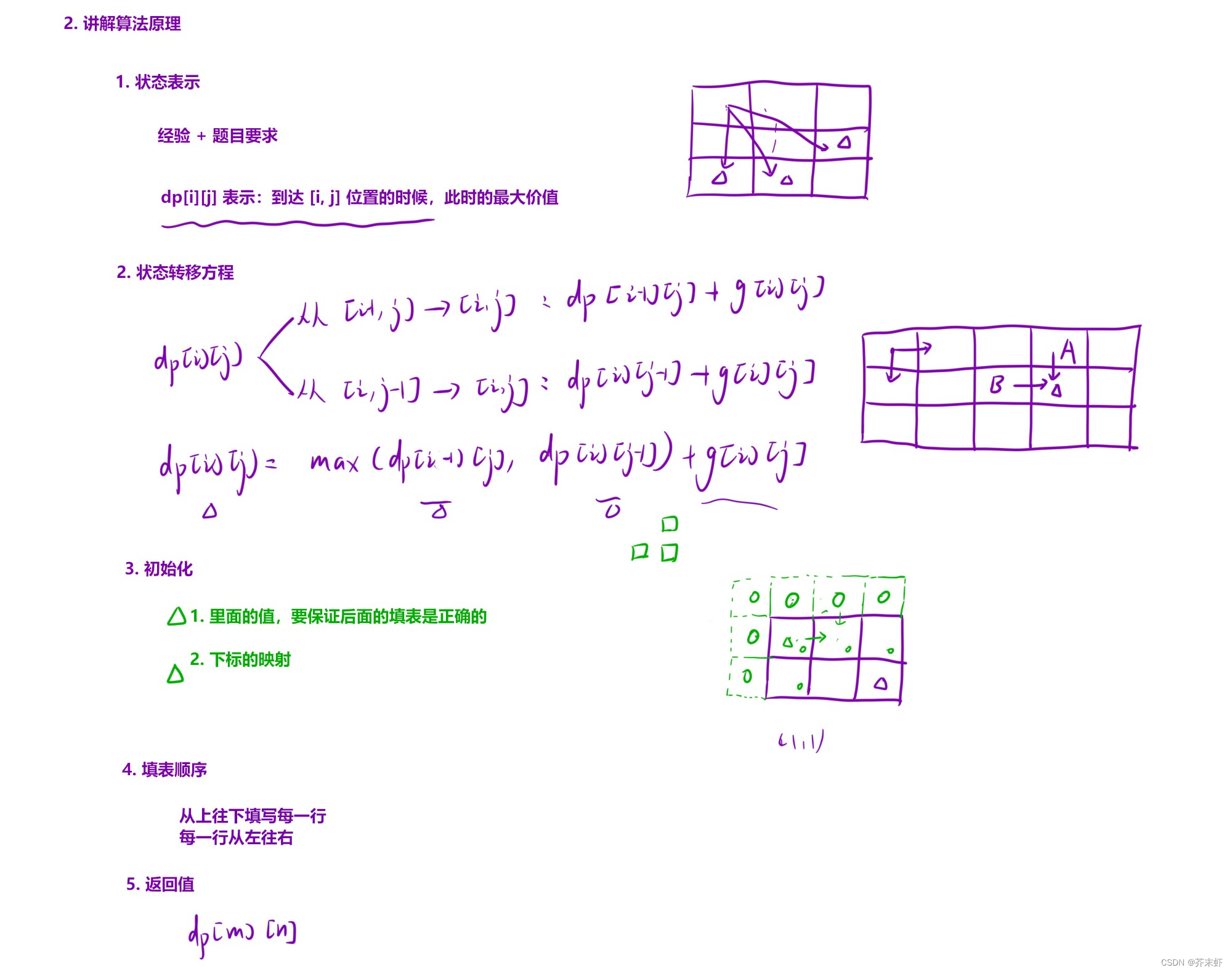
编写代码

class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {int m = frame.size(), n = frame[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1));for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){dp[i][j] = max(dp[i][j-1], dp[i-1][j])+frame[i-1][j-1];}}return dp[m][n];}
};

---

2.4 下降路径最小和

题目链接

931. 下降路径最小和 - 力扣（LeetCode）

题目描述

算法原理

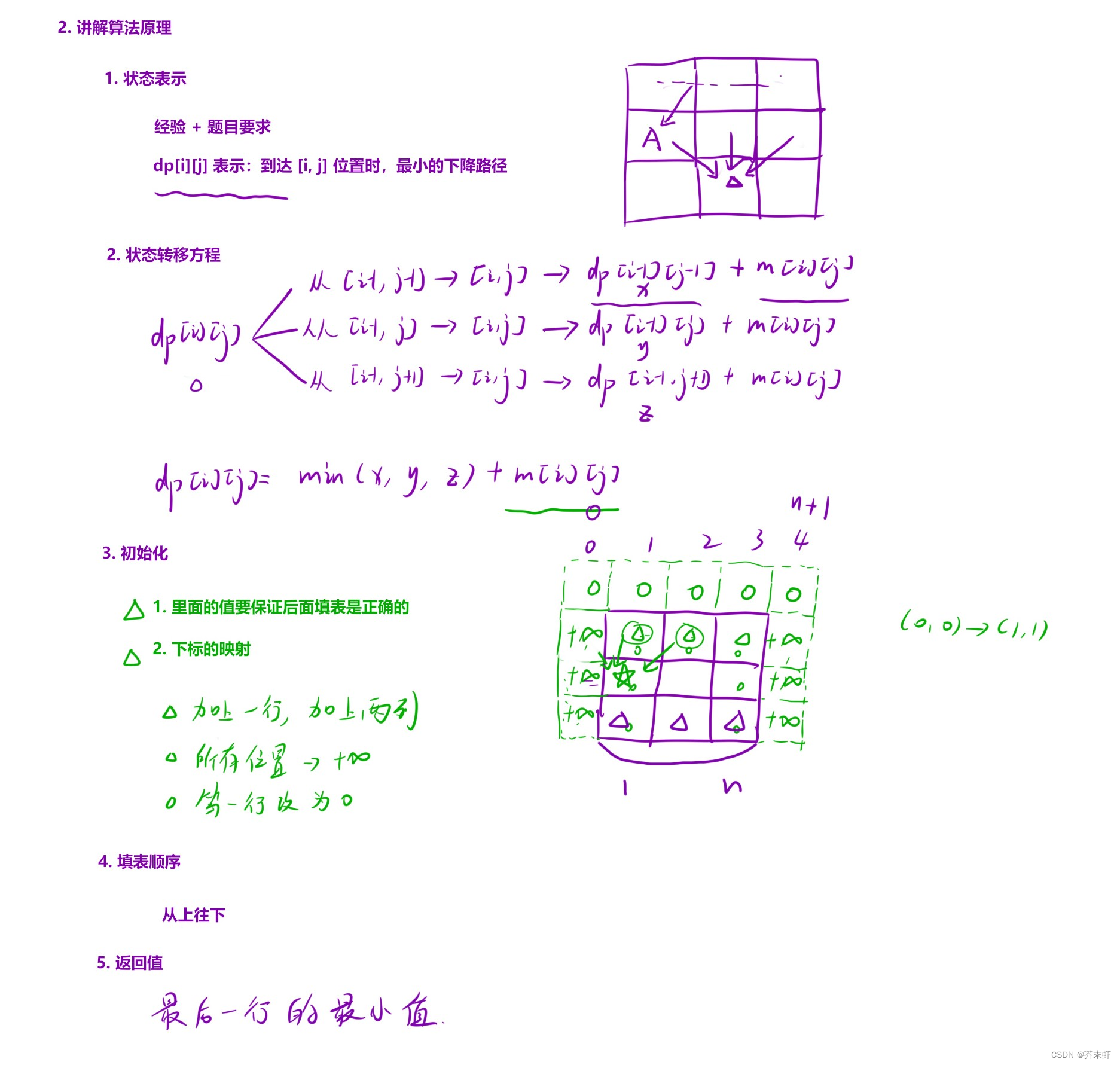
编写代码

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> dp(n+1, vector<int>(n+2, INT_MAX)); //dp表多创建1行2列for(int j = 0; j < n+2; ++j) //将第一行（虚拟节点）初始化为0，两边的两列初始化为INT_MAX{dp[0][j] = 0;}auto min = [](int a, int b, int c)->int{int tmp = a<b? a:b;return c<tmp? c:tmp;};for(int i = 1; i <= n; ++i) //从上往下填表{for(int j = 1; j <= n; ++j){dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1])+matrix[i-1][j-1];}}int ret = INT_MAX; //选出最后一行的最小值作为结果for(int j = 1; j <= n; ++j){if(ret>dp[n][j]){ret = dp[n][j];}}return ret;}};

---

2.5 最小路径和

题目链接

64. 最小路径和 - 力扣（LeetCode）

题目描述

算法原理

编写代码

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1, INT_MAX));dp[0][1] = dp[1][0] = 0;for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){dp[i][j] = grid[i-1][j-1] + min(dp[i-1][j], dp[i][j-1]);}}return dp[m][n];}
};

---

2.6 地下城游戏

题目链接

174. 地下城游戏 - 力扣（LeetCode）

题目描述

算法原理

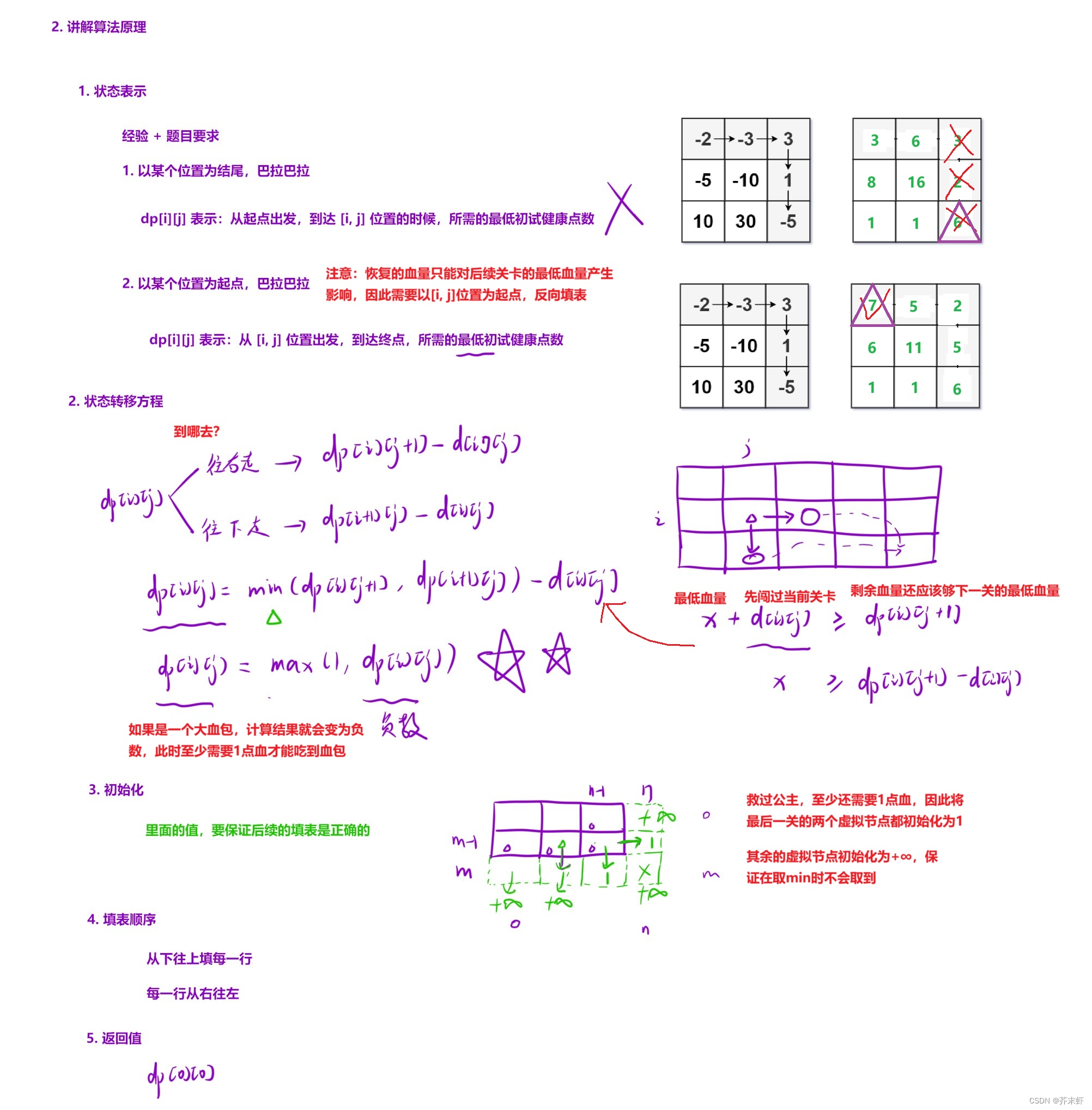
本题的难点在于怎么处理血量增加的问题, 增加血量不能为之前的损失提供帮助，只会对后续有帮助。
这意味着正向填表是困难的，但是反向填表很好做。以当前位置为起点，从后往前推，当前如果可以治愈，那么当前的最低血量就是下一关的最低血量减去治疗量，注意不可以<1。

编写代码

class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dun) {int m = dun.size(), n = dun[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1, INT_MAX));dp[m][n-1] = dp[m-1][n] = 1;for(int i = m-1; i >= 0; --i) //从下往上{for(int j = n-1; j >= 0; --j) //从右往左{dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dun[i][j];dp[i][j] = max(1, dp[i][j]);}}return dp[0][0];}
};

这篇关于【动态规划】路径问题 {二维动态规划；选择合适的状态表示方法；创建虚拟节点}的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---