本文主要是介绍复杂度分析(上):如何分析、统计算法的执行效率和资源消耗?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Tip:各平台的 markdown 解析标准不同,会有些数学符号无法识别,比如^n^: 表示n次方,~y~: 表示y 的底数。
什么是复杂度分析?
算法复杂度是指算法在编写成可执行程序后,运行时所需要的资源,资源包括时间资源和内存资源。
为什么需要复杂度分析?
首先任何一个程序最重要是准确性,即要确保程序能正常运行,实现预期功能。
但是,任何一个有价值的程序除了确保能正常运行,还要确保尽量短的运行时间和尽量少的运行空间,使程序正确高效执行得到预期效果。这就涉及时间复杂度分析和(空间复杂度分析),通过分析程序算法的时间复杂度可以找出运行时间尽量短的算法。
对于一些数据处理比较少的简单程序,不同算法使程序运行时间不同,但由于数据处理量少,这种运行时间的差别可以忽略。但是在实际应用中,很多程序往往涉及相当大量的数据处理,这就会导致实现同一个功能的程序,用不同算法,运行时间差别很大。有些算法可能只要几秒,有些算法却要几天才能得到结果。这时候,时间复杂度的分析就显得必要。
- 测试结果非常依赖测试环境
测试环境中硬件的不同会对测试结果有很大的影响。比如,我们拿同样一份代码,分别在 Intel Core i9处理器和 Intel Core i3处理器来运行,肯定 i9比 i3处理器快的多,同样一份代码,在不同的机器上,执行的速度会有不同。 - 测试接口受数据规模的影响很大
以排序算法为例,同一个排序算法,待排序数据的有序度不一样,排序的执行时间就会有很大的差别。极端情况,如果数据已经是有序的,那排序算法的不需要做任何操作,执行时间就会很短,如果测试数据规模调小,测试结果可能无法真实地反应算法的性能,比如,对于小规模的数据排序,插入排序可能反倒会比快速排序要快!
所以,我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率。
如何进行复杂度分析?
大 O 复杂度表示法
分析一下如下代码:
int cal(int n) {int sum = 0;int i = 1;for (; i <= n; ++i) {sum = sum + i;}return sum;}
从 CPU 角度拉看,这段代码的每一行都执行的类似的操作:读数据-运算-写数据。我们假设没喊代码的执行时间都一样,为 unit_time。在这个假设基础之上,这段代码总执行时间是多少呢?
第2、3行代码分别需要1个 unit_time 的执行时间,第4、5行都运行了 n 遍,所以需要2n*unit_time 的执行时间,所以这段代码总的执行时间就是(2n+2)*unit_time。可以看出来。
所有代码的执行时间 T(n) 与每行代码的执行次数成正比。
按照这个分析思路,再来看看这段代码。
int cal(int n) {int sum = 0;int i = 1;int j = 1;for (; i <= n; ++i) {j = 1;for (; j <= n; ++j) {sum = sum + i * j;}}}
我们还是同样假设每个语句的执行时间是 unit_time,那这段代码的总执行时间 T(n) 是多少呢?
第 2、3、4 行代码,每行都需要 1 个 unit_time的执行时间,第5、6行代码循环执行了 n 遍,需要2n * unit_time的执行时间,第7、8行代码循环执行了 n2 遍,所以需要2n2 *unit_time 的执行时间。所以,整段代码总的执行时间 T(n)=(2n2+2n+3)*unit_time。
尽管不知道 unit_time 的具体值,但是通过这两段代码执行时间推导,可以得到一个非常重要的规律:
所有代码的执行时间 T(n)与每行代码的执行次数 n 成正比。
用大 O 复杂度表示法:
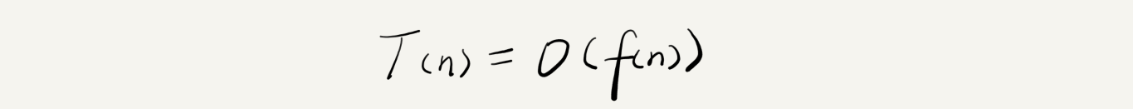
解释下这个公式:其中,T(n)我们已经讲过了,它表示代码执行的时间;n 表示数据规模的大小;f(n)表示每行代码执行的次数总和,因为这是一个公式,所以用 f(n)来表示。公式中 O,表示代码的执行时间T(n) 与 f(n) 表达式成正比。
所以,第一个例子中的 T(n) = O(2n+2),第二个例子中的 T(n) = O(2n2+2n+3)。这就是大 O 时间复杂度表示法。大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度,简称时间复杂度。
公式中低阶、常量、系数三部分并部左右增长趋势,所以可以忽略。用大 O 表示法表示上面两段代码:
T(n) = O(n) ; T(n) = O(n^2^)。
时间复杂度分析
- 只关注循环执行次数最多的一段代码
大 O 只是表示一种变化趋势,通常会忽略公式中低阶、常量、系数,只需要记录一个最大的量级就可以了,所以,我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那段代码就可以了。
看下面代码:
int cal(int n) {int sum = 0;int i = 1;for (; i <= n; ++i) {sum = sum + i;}return sum;}第2、3行代码都是常量级的执行时间,与 n 的大小无关,循环执行次数最多是4、5行,这两行代码被执行了 n 次
,所以总的时间复杂度就是 O(n)。
公式:T(n)=O(max(f(n),g(n)));
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
在分析如下代码:
int cal(int n) {int sum_1 = 0;int p = 1;for (; p < 100; ++p) {sum_1 = sum_1 + p;}int sum_2 = 0;int q = 1;for (; q < n; ++q) {sum_2 = sum_2 + q;}int sum_3 = 0;int i = 1;int j = 1;for (; i <= n; ++i) {j = 1; for (; j <= n; ++j) {sum_3 = sum_3 + i * j;}}return sum_1 + sum_2 + sum_3;}代码分为3部分,分别是 sum_1、sum_2、sum_3。
第一部分时间复杂多多少呢?这段代码执行了100次,是一个常量执行时间,跟 n 规模无关,可以忽略。
第二部分和第三部分的时间复杂度分别是 O(n)、O(n2)
综合这三段代码的时间复杂度,取其中量级最大部分,所以整段代码的复杂度就为 O(n2)。
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度乘积
看如下代码片段:
int cal(int n) {int ret = 0; int i = 1;for (; i < n; ++i) {ret = ret + f(i);} } int f(int n) {int sum = 0;int i = 1;for (; i < n; ++i) {sum = sum + i;} return sum;}
落实到具体的代码上,我们可以吧乘法法则看成是嵌套循环,
f()函数本身不是一个简单的操作,它的时间复杂度是 T(n)=O(n),因为是嵌套函数,所以整个 cal()函数的时间复杂度就是 T(n)=O(n2)=T1(n) * T2(n)。
几种常见的时间复杂度分析

复杂度量级可以分为多项式量级和非多项式量级。其中,非多项式量级只有两个:O(2n) 和 O(n!)。
对于多项式量级,随着数据规模的增长,算法的执行时间和空间占用统一呈多项式规律增长;而对于非多项式量级,随着数据规模的增长,其时间复杂度会急剧增长,执行时间无限增加;
下面主要来看看几种常见的多项式时间复杂度:
O(1)
一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
O(logn)、O(nlogn)
最难分析的是对数阶时间复杂度,这里通过一个例子来说明一下。
i=1;while (i <= n) {i = i * 2;}
根据我们前面讲的复杂度分析方法,第三行代码是循环执行次数最多的。所以,我们只要能计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。
从代码中可以看出,变量 i 的值从 1 开始取,每循环一次就乘以 2。当大于 n 时,循环结束。还记得我们高中学过的等比数列吗?实际上,变量 i 的取值就是一个等比数列。如果我把它一个一个列出来,就应该是这个样子的:

所以,我们只要知道 x 值是多少,就知道这行代码执行的次数了。通过 2x=n 求解 x 这个问题我们想高中应该就学过了,我就不多说了。x=log2n,所以,这段代码的时间复杂度就是O(log2n)。
把代码稍微再改一下,你看看这段代码的时间复杂度是多少?
i=1;while (i <= n) {i = i * 3;}
按照刚才的思路,很简单就能看出来,这段代码的时间复杂度 O(log3n)。
实际上,不管是以2为底、以3为底,还是以10为底,我们可以把所有对数阶的时间复杂度都记为 O(logn)。为什么呢?
我们知道,对数之间是可以互相转换的:
log3n 就等于 log32 * log2n,所以 O ( log3n) = O(C * log2n),其中
C=log32 是一个常量。
基于我们前面的一个理论:在采用大 O 标记复杂度的时候,可以忽略系数,即 O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于 O(log3n)。因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)。
如果你理解了前面讲的 O(logn),那 O(nlogn)就很容易理解了。还记得我们刚讲的乘法法则吗?如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,时间复杂度就是 O(nlogn) 了。而且,O(nlogn) 也是一种非常常见的算法时间复杂度。比如,归并排序、快速排序的时间复杂度都是 O(nlogn)。
O(m+n)、O(m*n)
再来讲一种跟前面都不一样的时间复杂度,代码的复杂度由两个数据的规模来决定。比如:
int cal(int m, int n) {int sum_1 = 0;int i = 1;for (; i < m; ++i) {sum_1 = sum_1 + i;}int sum_2 = 0;int j = 1;for (; j < n; ++j) {sum_2 = sum_2 + j;}return sum_1 + sum_2;
}从代码中可以看出,m 和 n 是表示两个未知的数据规模,其大小关系也无法确定,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是 O(m+n)。
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为:T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效:T1(m)*T2(n) = O(f(m) * f(n))。
综上所述:
多项式阶:随着数据规模的增长,算法的执行时间和空间占用,按照多项式的比例增长。包括,
O(1)(常数阶)、O(logn)(对数阶)、O(n)(线性阶)、O(nlogn)(线性对数阶)、O(n2)(平方阶)、O(n3)(立方阶)
非多项式阶:随着数据规模的增长,算法的执行时间和空间占用暴增,这类算法性能极差。包括,
O(2n)(指数阶)、O(n!)(阶乘阶)
空间复杂度分析
相比起时间复杂度分析,空间复杂度分析方法学起来就非常简单了。
这里也举一个例子进行说明:
void print(int n) {int i = 0;int[] a = new int[n];for (i; i <n; ++i) {a[i] = i * i;}for (i = n-1; i >= 0; --i) {print out a[i]}
}这里第 3 行申请了一个大小为 n 的 int 类型数组,除此之外,其余代码所占空间都是可以忽略的,所以整段代码的空间复杂度就是 O(n)。
我们常见的空间复杂度就是 O(1)、O(n)、O(n^2 ),像 O(logn)、O(nlogn) 这样的对数阶空间复杂度平时都用不到,相比起来,空间复杂度分析比时间复杂度分析要简单很多。
内容小结
复杂度包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系,越高阶复杂度的算法,执行效率越低。常见的复杂度从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )。
refer to
学习总结资料来自极客时间版权所有: https://time.geekbang.org/column/article/40036
这篇关于复杂度分析(上):如何分析、统计算法的执行效率和资源消耗?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






