中国剩余定理——AcWing 204. 表达整数的奇怪方式

本文主要是介绍中国剩余定理——AcWing 204. 表达整数的奇怪方式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

中国剩余定理

定义

中国剩余定理最早出自我国古代的《孙子算经》，是数论中的一个重要定理。它描述了这样一种情况：在模运算下，对于一组线性同余方程组，存在唯一解的条件和求解方法。

运用情况

常用于在一些涉及到按不同模的余数条件下求解问题。比如在密码学、计算数论、计算机科学等领域中，当需要处理多个模条件相关的计算时，常常会用到中国剩余定理。

注意事项

• 要求各个模之间互质，否则定理不直接适用，可能需要进行一些转化处理。
• 在计算过程中要保证计算的准确性，尤其是涉及到较大数的运算时。

解题思路

AcWing 204. 表达整数的奇怪方式   

题目描述

AcWing 204. 表达整数的奇怪方式 - AcWing

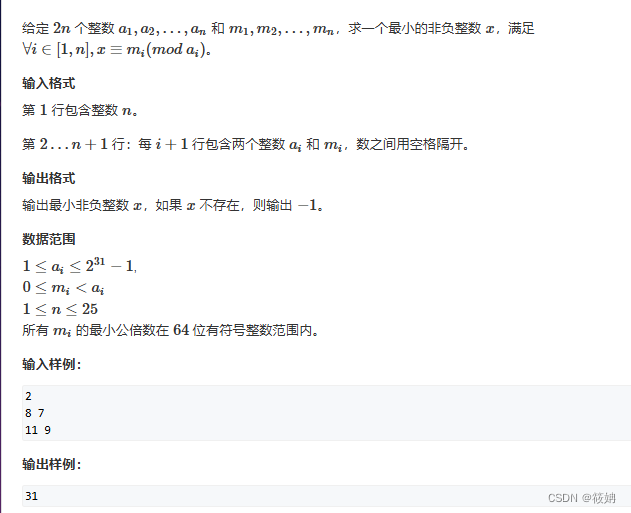
运行代码

#include <iostream>
#define int long long
using namespace std;
int n;
int exgcd(int a, int b, int &x, int  &y)
{if(!b){x = 1, y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= a / b * x;return d;
}
signed main()
{bool st = true;cin >> n;int a1, m1;cin >> a1 >> m1;for(int i = 2; i <= n; i ++ ){int a2, m2, k01, k02, d;cin >> a2 >> m2;d = exgcd(a1, a2, k01, k02);if((m2 - m1) % d) {st = false;break;}k01 = k01 * (m2 - m1) / d;k01 = (k01 % (a2 / d) + (a2 / d)) % (a2 / d);m1 += a1 * k01;a1 = a1 / d * a2;}if(st) cout << (m1 % a1 + a1) % a1 << endl;else cout << -1 << endl;return 0;
} 

代码思路

1. 类型定义与变量初始化：

   • 使用 #define int long long 将整型变量默认定义为长整型，以处理大数。
   • 定义全局变量 n 表示同余方程的数量。

2. 扩展欧几里得算法（exgcd）： 实现了扩展欧几里得算法，用于求解形如 ax + by = gcd(a, b)ax+by=gcd(a,b) 的方程。返回值 d 是 aa 和 bb 的最大公约数（GCD），同时通过引用参数 x 和 y 返回系数。这个函数是解决CRT的关键，用于寻找模数之间的关系。

3. 主函数（main）：

   • 首先读入同余方程的数量 n。
   • 初始化第一个方程的系数 a1 和模数 m1。
   • 对于每个后续的方程（从第二个到第 n 个），执行以下操作：
     • 读取当前方程的系数 a2 和模数 m2。
     • 使用 exgcd 函数计算 a1 和 a2 的最大公约数 d，以及对应的系数 k01, k02。
     • 检查是否存在解：如果 (m2 - m1)(m2−m1) 不能被 d 整除，则说明无解，标记 st 为 false 并跳出循环。
     • 如果有解，根据中国剩余定理调整 m1 和 a1，使得它们分别表示合并后的同余方程的临时解和新模数。
   • 最后，根据 st 的值输出结果：如果为 true，则输出满足所有同余条件的最小非负整数解；否则，输出 -1 表示无解。

改进思路

1. 使用更明确的变量名：虽然简短的变量名让代码紧凑，但更具有描述性的名称可以提高代码的可读性。例如，可以将 a1, a2, m1, m2 等变量名改为 current_coefficient, next_coefficient, current_modulus, next_modulus 等。

2. 避免全局变量：全局变量 n 可能导致代码的维护和理解难度增加，尤其是在大型项目中。可以考虑将其作为函数参数传递。

3. 优化解的计算和输出：

   • 直接计算最终解而不仅仅是累积操作。在循环结束后，可以计算最终的 x（即满足所有同余方程的解）并直接取模，避免最后对 a1 进行额外的模运算。
   • 输出解时，使用 % 运算符可能两次取模，实际上 (m1 % a1 + a1) % a1 可以简化为 (m1 % a1)，因为当 m1 < 0 时，(m1 + a1) % a1 已经保证结果非负。

4. 增加错误处理和注释：对于输入验证（如检查模数是否两两互质、是否为正整数等）添加更多的错误处理逻辑，并在关键步骤添加注释，帮助读者理解算法逻辑。

5. 模块化设计：将中国剩余定理的求解过程封装成一个独立的函数，而不是全部放在 main 函数中，这样可以提高代码的复用性和可测试性。

6. 考虑大数运算库：如果要处理非常大的数字，可以考虑使用专门的大数运算库（如 GMP 库），这会比直接使用 C++ 内置数据类型更高效且支持更大的数值范围。

7. 优化扩展欧几里得算法的实现：虽然现有实现是标准的，但在某些特定情况下，可以通过一些小技巧进一步优化，比如利用幂次计算减少递归深度，或是迭代法替代递归以节省栈空间。

这篇关于中国剩余定理——AcWing 204. 表达整数的奇怪方式的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---