【数据结构】第十七弹---C语言实现选择排序

本文主要是介绍【数据结构】第十七弹---C语言实现选择排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

✨个人主页：熬夜学编程的小林

💗系列专栏：【C语言详解】【数据结构详解】【C++详解】

1、选择排序

1.1、基本思想

1.2、代码实现

1.3、代码测试

1.4、时空复杂度分析

总结

1、选择排序

1.1、基本思想

选择排序是一种简单直观的比较排序算法。该算法的基本思想是在每一轮中选出当前未排序部分的最小（或最大）元素，然后将其放置到未排序序列的起始位置，这个过程一直重复直至整个数组被排序。

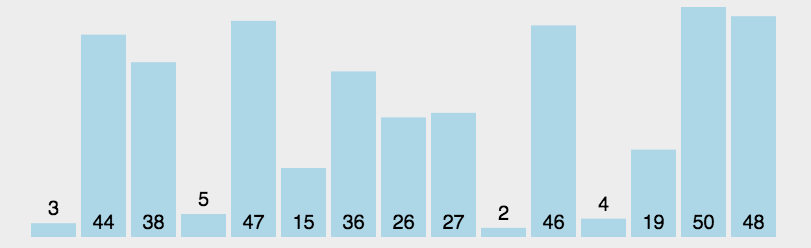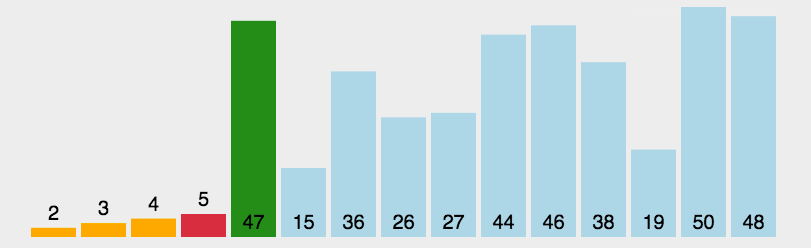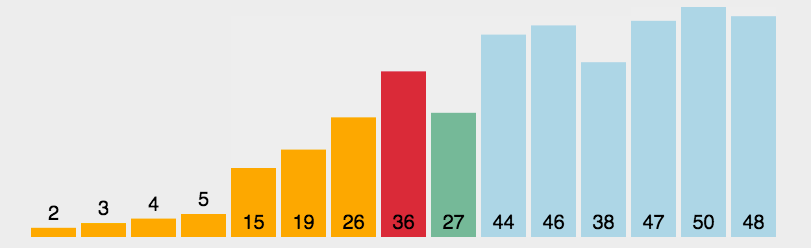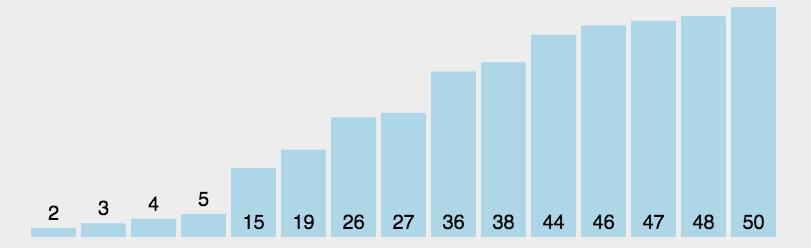
选择排序的具体步骤如下：

★ 从数组的当前未排序部分选择最小（或最大）的一个元素。
★ 将这个最小（或最大）元素与未排序序列的第一个元素交换位置。
★ 然后从剩余未排序的元素中继续这个过程，将每一次找到的最小（或最大）元素放到未排序序列的开始。
★ 这个过程一直进行到整个数组的所有元素都被排为有序状态。

1.2、代码实现

此处可以进行一个小的优化，同时找最小值与最大值，但是有一个细节需要注意，先上代码。

此处还需要交换元素，所以提前封装一个交换函数。

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void SelectSort(int a[], int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxi = begin;//找最大值的下标int mini = begin;//找最小值的下标for (int i = begin + 1; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);Swap(&a[end], &a[maxi]);begin++;end--;}
}

★ 首先初始化两个索引begin和end，分别代表当前未排序序列的开始和结束位置。

★ 进入一个循环，条件是begin < end，确保在数组中还有未排序的元素。

★ 遍历一遍序列，找到最大元素和最小元素的下标。

★ 将最小元素与序列的始端交换，最大元素与序列的尾端交换。

★ 更新begin与end。

思考一下上面写的代码有没有问题呢？？？

答案是有问题的，因为这里我们是首先进行最小元素与首位置更换，再进行最大元素与末尾更换，如果我的最大元素就在首位置就会有问题，如下图：

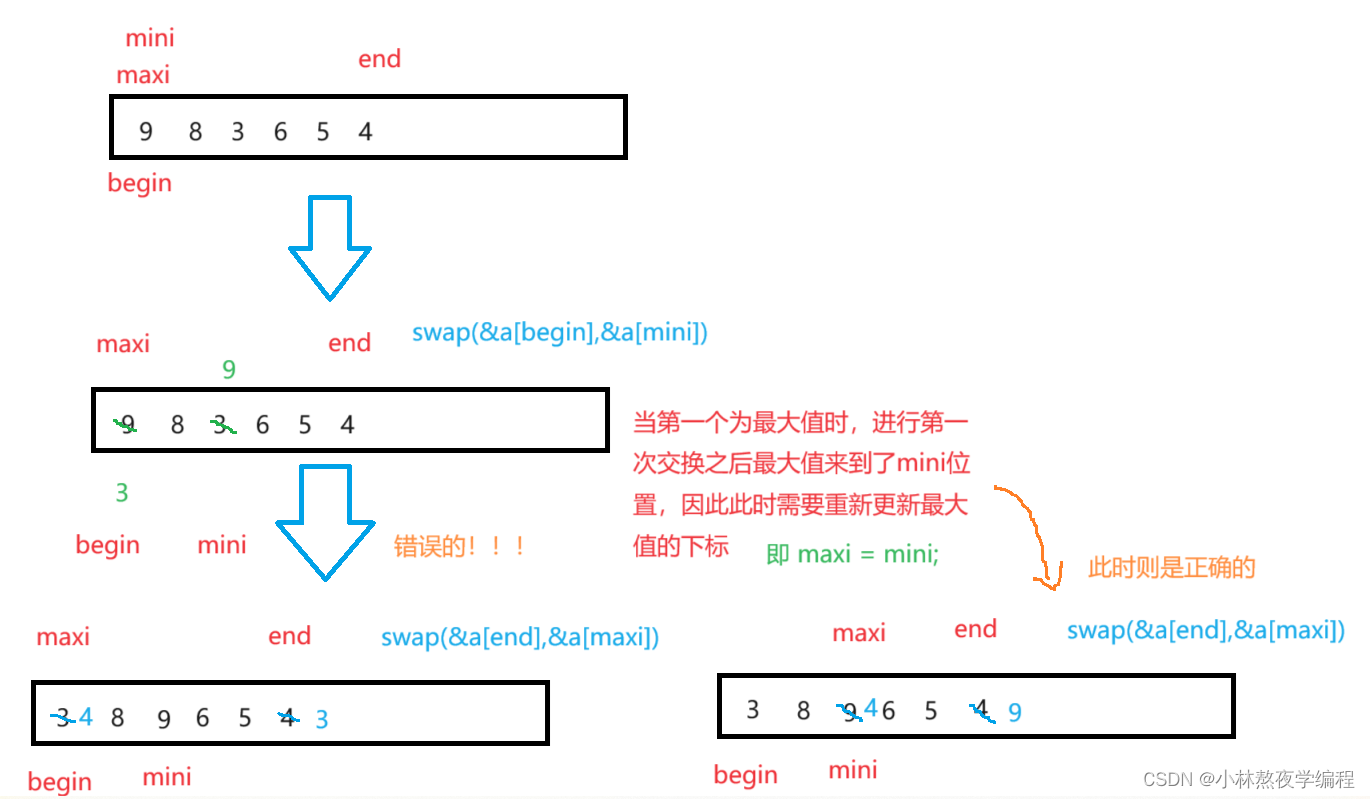
如果最大值就在第一个位置时需要更新最大值的下标！！！

正确的代码如下：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void SelectSort(int a[], int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxi = begin;//找最大值的下标int mini = begin;//找最小值的下标for (int i = begin + 1; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);//最大值的位置跟最小值重合//mini被换到maxi位置时  原本的最大值则是miniif (maxi == begin)maxi = mini;Swap(&a[end], &a[maxi]);begin++;end--;}
}

注意：

1.这里是对最初的选择排序进行优化，最小值最大值一起进行的。

2.当最大值被交换后，需要重新赋值。

1.3、代码测试

测试代码：

//测试选择排序
int main()
{int a[] = { 9,8,7,6,5,4,3,2,1,0 };//给一组数据int sz = sizeof(a) / sizeof(a[0]);//计算数组元素个数printf("排序前：\n");ArrayPrint(a, sz);SelectSort(a, sz);printf("排序后：\n");ArrayPrint(a, sz);return 0;
}

测试结果：

1.4、时空复杂度分析

时间复杂度

最好、平均、最坏情况下的时间复杂度都是 O(n^2)。

原因在于，不管数组的初始顺序如何，选择排序都需要比较所有未排序的元素来找到最小（或最大）的元素，并执行这个过程 n-1 次（对于 n 个元素的数组）。每次选择操作需要比较的次数从 n-1 次减少到 1 次，总共的比较次数是 (n-1) + (n-2) + … + 1 = n(n-1)/2，这是一个二次函数，因此时间复杂度为 O(n^2)。

空间复杂度

选择排序是一种原地排序算法，除了输入数组外，它只需要有限的几个变量（比如，用于存储最小元素下标的变量和循环计数器）。因此，它的空间复杂度为常数空间O(1)。

选择排序的特性总结：