红黑树的基本概念

本文主要是介绍红黑树的基本概念，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

红黑树

特征
- [1] 根节点是黑色的
- [2] 每个叶子节点都是黑色的空节点(NIL), 也就是说，叶子节点不存储数据
- [3] 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的
- [4] 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点

为什么说红黑树是“近似平衡”的？

平衡的意思可以等价为性能不退化
近似平衡就是等价为性能不会退化太厉害
二叉查找树很多操作的性能都跟树的高度成正比
- 一颗极其平衡的二叉树(满二叉树或完全二叉树)的高度大约是log2n
- 所以，如果要证明红黑树是近似平衡的，只需要分析，红黑树的高度是否比较稳定地趋近log2n就好了
红黑树高度分析
- 如果，把红色节点从红黑树中去掉，那单纯包含黑色节点的红黑树的高度是多少？
  - 红色节点删除之后，有些节点就没有父节点了，它们会直接拿这些节点的祖父节点(父节点的父节点)作为父节点。所以，之前的二叉树就会变成四叉树
  - 前面红黑树的定义有一条：从任意节点到可达的叶子节点的每个路径包含相同数目的黑色节点。从四叉树中取出某些节点，放到叶节点位置，四叉树就变成完全二叉树。所以，仅包含黑色节点的四叉树的高度，比包含相同节点个数的完全二叉的高度还要笑
  - 完全二叉树的高度近似log2n,这里的四叉“黑树”的高度要低于完全二叉树，所以去掉红色节点的“黑树”的高度也不会超过log2n
  - 原红黑树中。红色节点不能相邻，也就说，有一个红色节点就要至少有一个黑色节点，将它跟其他红色节点隔开。红色树中包含最多黑色节点的路径不会超过log2n,所以加入红色节点之后，最长路径不会超过2log2n也就是说红黑树的高度近似2log2n

红黑树操作项

左旋(rotate left)
- 左旋全称，围绕某个节点的左旋
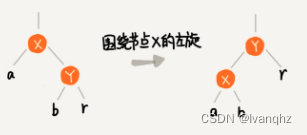
- X的右子节点成为X的父节点。也即X成为左子节点
右旋(rotate right)
- 右旋全称，围绕某个节点的右旋
- X的左子节点成为X的父节点。也即X成为右子节点
插入操作的平衡调整
- 红黑树规定，插入的节点必须是红色。二叉查找树中新插入的节点都是放在叶子节点上
  - 如果插入节点的父节点是黑色，那什么都不用做，它仍然满足红黑树的定义
  - 如果插入的节点是根节点，那直接改变它的颜色，把它变成黑色
- 如果存在违背红黑树的定义，就需要左右旋转和改变颜色做调整
- 红黑树的平衡调整过程是一个迭代的过程
  - 把正在处理的节点叫做关注节点
  - 关注节点会随着不停迭代处理，而不断发生变化。最开始的关注节点就是新插入的节点
- 插入平衡调整策略
  - CASE 1: 如果关注节点a，它的叔叔节点d是红色
    - 操作策略
      - 将关注节点a的父节点b, 叔叔节点d的颜色都设置成黑色
      - 将关注节点a的祖父节点c设置成红色
      - 关注节点变成a的祖父节点c
      - 跳到CASE 2 或 CASE 3
    - 策略说明
      - a 和 b都是红色，违背了特征[3]. 把b设置成黑色以解决问题
      - b 从 红色变成了黑色，违背了特征[4].所以要把c设置红色
      - 因为a,c都改变了颜色。导致 d节点分支的黑色节点总数减少了1，违背了特征[4].所以d要变成黑色
  - CASE 2: 如果关注节点是a，它的叔叔节点d是黑色，关注节点a是其父节点b的右子节点
    - 操作策略
      - 关注节点变成节点a的父节点b
      - 围绕新的关注节点b左旋
      - 跳到CASE 3
    - 策略说明
      - 处理红黑树的核心思想：将红色的节点移到根节点，然后将根节点设为黑色
      - 所以要不断将破坏红黑树特性的红色节点上移。即通过左旋将a上移
      - 如果a变成了根节点，可以直接变黑色.如果不是根节点，就需要切换关注节为b
      - 处理问题准则
        需要从下至上(由叶到根)方向处理
        必须先解决子节点的问题，再解决父节点问题
  - CASE 3: 如果关注节点是a，它的叔叔节点d是黑色，关注节点a是其父节点b的左子节点
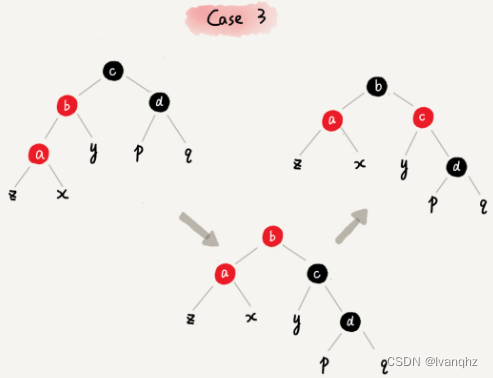
    - 操作策略
      - 围绕关注节点a的祖父节点c右旋
      - 将关注节点a的父节点b，兄弟节点c的颜色互换
      - 调整结束
    - 策略说明
      - b 和 a都是红色，违背了特征[3]
      - 所以把b，c颜色互换。b为黑色, c为红色。然后以c右旋
        b设置为黑色,解决了特征[3]
        b为黑色后，所有经过b的黑色节点数量增加了1，违背了特征[4]，要把c改成红色，
        但是经过d的黑色节点数量减少了1，然后以c右旋
- 删除平衡调整
  - 删除平衡调整分两步
    - 针对删除节点初步调整
      - 将红黑树当作一颗二叉查找树，将节点删除后，可能违反特征[1], 特征[3], 特征[4]
      - 对于删除的某节点(删除节点y，新节点x)
        删除节点y之后，x占据了原来节点y的位置
        既然删除y(y是黑色)，意味着减少一个黑色节点，那在该位置上增加一个黑色即可
        假设"x包含一个额外的黑色"，就正好弥补了"删除y所丢失的黑色节点"，就不会违反特征[4]
        还有，假设"x包含一个额外的黑色"(x原本颜色还存在)，这样也不会违反特征[4]
        现在，x不仅包含原本的颜色属性，x还包含一个额外的黑色。即x的颜色属性是"红 + 黑" 或 “黑 + 黑”，违反特征[3]
    - 针对关注节点进行二次调整
      - 二次调整是为了解决违反特征[3],特征[4]这2个特征
      - 调整方法(x为需要调整的节点)：将x所包含的额外的黑色不断沿树上移(向根方向移动)
        x是 "红 + 黑"节点，x为叶子节点
        直接把x设为黑色，结束。此时红黑树性质全部恢复
        
        x是 "黑 + 黑"节点，且x是根
        什么都不做，结束。此时红黑树性质全部恢复
        
        x是"黑 + 黑"节点，且不是根
        可以划分出四种子情况
  - 针对删除节点初步调整
    - 删除简述
      - 被删除节点没有儿子，即为叶节点。那么，直接将该节点删除就OK了
      - 被删除节点只有一个儿子。那么，直接删除该节点，并用该节点的唯一子节点顶替它的位置
      - 被删除节点有两个儿子
        先找出它的后继节点，然后把‘它的后继节点的内容’复制给‘该节点的内容’，之后，删除‘它的后继节点’
    - CASE 1: 如果要删除的节点是a, 它只有一个子节点b
      - 操作策略
        
        删除节点a，并且把节点替换到a的位置，这一部分操作跟普通的二叉查找树的删除操作一样
        节点a只能是黑色，节点b也只能是红色，其他情况均不符合红黑树的定义。这种情况下，我们把节点b改成黑色
        调整结束，不需要进行二次调整
      - 策略说明
        
        被删除节点只有一个儿子
        那么，直接删除该节点，并用该节点的唯一字节点顶替他的位置
    - CASE 2: 如果要删除的节点a有两个非空子节点，并且它的后继节点就是节点a的右子节点c
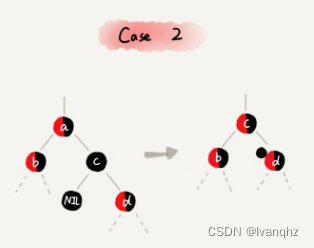
      - 操作策略
        
        如果节点a的后继节点就是右子节点c，那右子节点肯定没有左子树。我们把节点a删除，并且将节点c替换到节点a的位置。这一部分操作跟普通的二叉树的删除操作无异
        然后把节点c的颜色设置为跟节点a相同的颜色
        如果节点c是黑色，为了不违反红黑树的特征[4],我们给节点c的右子节点d多加一个黑色，节点d就成了"红 - 黑" 或"黑 - 黑"
        同时关注节点变成了节点d，第二步的调整操作就会针对关注节点来做
      - 策略说明
        
        被删除的节点有两个儿子。那么，先找出它的后继节点
        然后把“它的后继节点的内容”复制给“该节点的内容”
        之后，删除“它的后继节点”。在这里，后继节点详单于替身，在将后继节点的内容复制给“被删除节点”之后，再将后继节点删除
        这样就巧妙的将问题转换为“删除后继节点”的情况了
        后面只需要考虑后继节点的情况
    - CASE 3: 如果要删除的是节点a，它有两个非空子节点，并且节点a的后继节点不是右子节点
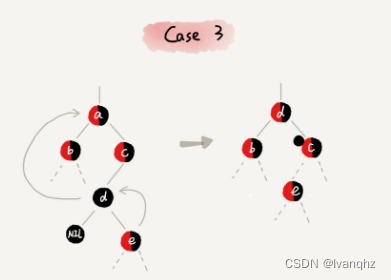
      - 找到后继节点d，并将它删除，删除后继节点d的过程参照CASE 1
      - 将节点a替换成后继节点d
      - 把节点d的颜色设置为跟节点a相同的颜色
      - 如果节点d是黑色，为了不违法特征[4],我们给节点d的右子节点c多加一个黑色，这个时候节点c就变成了"红 - 黑" 或者 "黑 - 黑"
      - 这个时候，关注节点变成了节点c，第二步的调整操作就会针对关注节点来做
  - 针对关注节点进行二次调整
    - 经过初步调整之后，关注节点变成了“红 - 黑” 或者 “黑 - 黑”
    - CASE1: 如果关注节点是a，它的兄弟节点c是红色
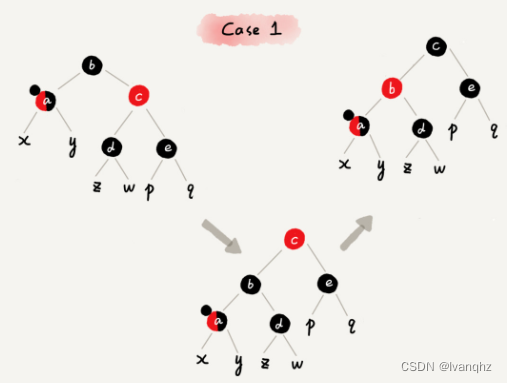
      - 操作策略
        
        围绕关注节点a的父节点b左旋
        关注节点a的父节点b和祖父节点c交换颜色
        关注节点不变
        继续从四种情况中选择合适的规则来调整
      - 策略说明
        
        这样做的目的是将CASE 1 转换为CASE 2, CASE 3 或 CASE 4从而进一步处理
        对b进行左旋。左旋后，为了保持红黑树特性，就需要把 b，c的颜色互换
    - CASE 2: 如果关注节点是a，它的兄弟节点c是黑色，并且节点c的左右子节点d，e都是黑色
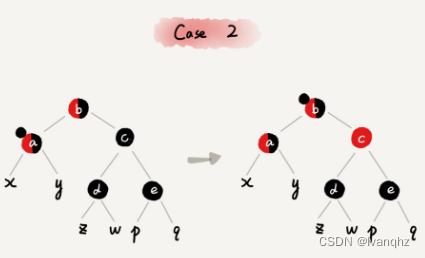
      - 操作策略
        
        将关注节点a的兄弟节点c的颜色变成红色
        从关注节点a中去掉一个黑色，这个时候节点a就是单纯的红色或者黑色
        给关注节点a的父节点b添加一个黑色，这个时候节点b就变成来"红-黑" 或者"黑 - 黑"
        关注节点从a变成其父节点b
        继续从四种情况中选择符合的规则来调整
      - 策略说明
        
        这个情况的处理思想是把"a中多余的一个黑色属性上移(往根节点方向)"
        假设a为"黑 + 黑"节点，将a由"黑 + 黑"节点变成"黑"节点，多余的一个"黑"属性，转移到父节点
        b节点多出了一个黑属性(如b原先是"黑"，则此时变成了"黑 + 黑"；若b原先是红，则变成"红 + 黑")
        此时，所有经过a分支中黑色节点个数没变化
        因为经过c分支黑色节点个数+1了，需要把黑色数量-1。所以，要把 c设置为红色
    - CASE 3: 如果关注节点是a，它的兄弟节点c是黑色，c的左子节点d是红色，c的右子节点e是黑色
      - 操作策略
        
        围绕关注节点a的兄弟节点c右旋
        节点c和节点d交换颜色
        关注节点不变
        跳转到CASE 4,继续调整
      - 策略说明
        
        主要是为了把CASE 3 转换成CASE 4
        对c进行右旋。为了保证右旋后仍然是红黑树，需要c和d交换颜色
        这个时候变成了平衡二叉树的单旋和双旋的情况，双旋的处理逻辑就是把双旋变成单旋(比如先右后左旋就是把树变成'左撇子')
    - CASE 4: 如果关注节点a的兄弟节点c是黑色，并且c的右子节点是红色的
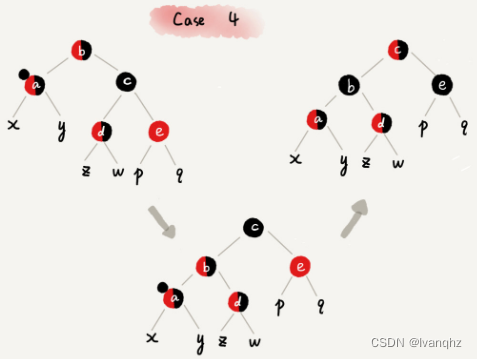
      - 操作策略
        
        围绕关注节点a的父节点b左旋
        将关注节点a的兄弟节点c的颜色，跟关注节点a的父节点b设置成相同的颜色
        将关注节点a父节点b的颜色设置为黑色
        从关键节点a中去掉一个黑色，节点a变成单纯的红色或黑色
        将关注节点a的叔叔节点e设置为黑色
        调整结束
      - 策略说明
        
        目的：去除"黑-黑"/"红-黑"节点，变成单独的黑色节点
        左旋后为什么把 b设置成c的颜色？
        因为左旋后，把和b和d都是红色违反特征[3]
        如果都是黑色都违反特征[4]
        
        设置b为黑色，为了保证满足特征[4]
        “同时经过根节点和a分支的黑色节点个数不变”
        只需要a丢弃多余的颜色。假设a的颜色"黑 + 黑"，而左旋后"同时经过根节点和a分支的黑色节点"增加了1
        现在，只需要将a由"黑 + 黑"变成单独的"黑"节点
        
        “同时经过根节点和d的分支的黑色节点不变”
        若要满足这个条件,只需要把b的原始颜色给c即可
        所以，最后算是对调了b和c的颜色
        
        “同时经过根节点和e分支的黑色节点不变”
        在满足上一个条件下。要满足这个条件。把e设置成黑色即可