本文主要是介绍关于二分法的理解(以JS为例),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
算法介绍
基本概念
二分查找算法,又称折半查找算法,是一种在有序数组中查找特定元素的高效方法。它的核心思想是将数组分成两半,然后根据目标值与中间元素的比较结果来决定是继续在左半部分还是右半部分进行搜索。
工作原理
- 初始化:设置两个指针,一个指向数组的起始位置(low),另一个指向数组的结束位置(high)。
- 循环:当low指针小于或等于high指针时,执行以下步骤:
- 计算中间位置(mid),通常使用
(low + high) / 2。 - 比较中间元素(arr[mid])与目标值。
- 如果中间元素等于目标值,返回中间位置,查找成功。
- 如果中间元素大于目标值,说明目标值位于数组的左半部分,更新high指针为mid - 1。
- 如果中间元素小于目标值,说明目标值位于数组的右半部分,更新low指针为mid + 1。
- 计算中间位置(mid),通常使用
- 结束条件:当low指针大于high指针时,循环结束,表示目标值不在数组中。
时间复杂度
二分查找算法的时间复杂度为O(log n),其中n是数组的长度。这是因为每次迭代都会将搜索范围减半,因此需要对数级次迭代才能找到目标值或确定它不存在。
空间复杂度
二分查找算法的空间复杂度为O(1),因为它只需要常数级别的额外空间来存储索引。
适用条件
二分查找算法要求数组必须是有序的。如果数组是无序的,那么在应用二分查找之前,需要先对其进行排序,这将增加算法的总体时间复杂度。
优点
- 高效:对于大型数据集,二分查找比线性搜索更快。
- 简单:算法逻辑清晰,易于理解和实现。
局限性
- 需要有序数组:如果数组无序,需要先排序,这可能会影响性能。
- 不适用于动态数据集:如果数组经常变动,维护其有序状态可能会很复杂。
通俗讲解
二分查找算法:就像在书架上找书
想象一下,你在一个按字母顺序排列的书架上找一本特定的书。书架上有成千上万本书,但它们都是有序排列的。二分查找算法就像是你快速找到这本书的方法。
- 开始搜索:你站在书架的中间,看看那里的书是不是你要找的。
- 缩小范围:如果那本书的书名比你要找的书的书名要早,你就会往右边看。如果晚,就往左边看。
- 重复过程:不管你往左还是往右,你都会再次站在新的中间位置,重复刚才的比较过程。
- 直到找到:这个过程会一直重复,直到你找到那本书,或者确定书架上没有这本书。
为什么它这么快?
- 分而治之:每次你只需要看一半的书,而不是全部。这就像是你每次翻页都跳过一半的内容,大大加快了查找速度。
- 对数级速度:因为每次你都在减少一半的搜索范围,所以查找的速度非常快。这就是为什么我们说它的时间复杂度是O(log n),n是书的数量。想象一下,1000本书,你可能只需要10次就能找到,而不是1000次。
但是,有个前提
- 书架要有序:这个方法只有在书架上的书籍是有序排列的情况下才有效。如果书架乱七八糟,这个方法就不管用了。
用在计算机上
在计算机科学中,二分查找算法用在有序数组中查找特定元素。计算机就像你一样,通过比较中间的元素和它要查找的目标值,然后决定是继续在数组的哪一半查找,直到找到目标或者确定它不存在。
总结
二分查找算法就像是在有序的书架上快速找到一本书的技巧。它简单、高效,但需要一个有序的环境。下次当你需要在大量有序的数据中快速找到某个元素时,不妨想想这个算法,它可能会帮你节省很多时间。
核心思想
-
有序性:二分查找算法的基础是数据的有序性。只有当数据集(如数组)是有序的,算法才能有效工作。
-
中间点:算法通过计算数组中间的索引来找到一个参考点,即中间元素。
-
比较与决策:将目标值与中间元素进行比较。根据比较结果,算法决定是继续在当前搜索区间的左侧还是右侧进行查找。
-
区间减半:无论比较结果如何,都会将搜索范围缩小到原来的一半。如果目标值小于中间元素,搜索区间将变为左侧一半;如果目标值大于中间元素,搜索区间将变为右侧一半。
-
迭代:这个过程会不断重复,每次迭代都会更新搜索区间的边界,直到找到目标值或搜索区间为空。
-
效率:通过每次迭代将搜索区间减半,二分查找算法能够非常快速地定位元素或确定元素不存在,其效率远高于线性搜索。
-
终止条件:搜索终止的条件有两个:找到目标值或搜索区间为空(即low指针大于high指针)。
-
简单性:算法的逻辑简单明了,易于实现和理解。
-
普适性:虽然二分查找算法在数组上最为常见,但其核心思想可以应用于其他有序数据结构的搜索问题。
-
局限性:算法的局限性在于它要求数据必须是事先排序的。如果数据动态变化,需要重新排序,这可能会影响算法的效率。
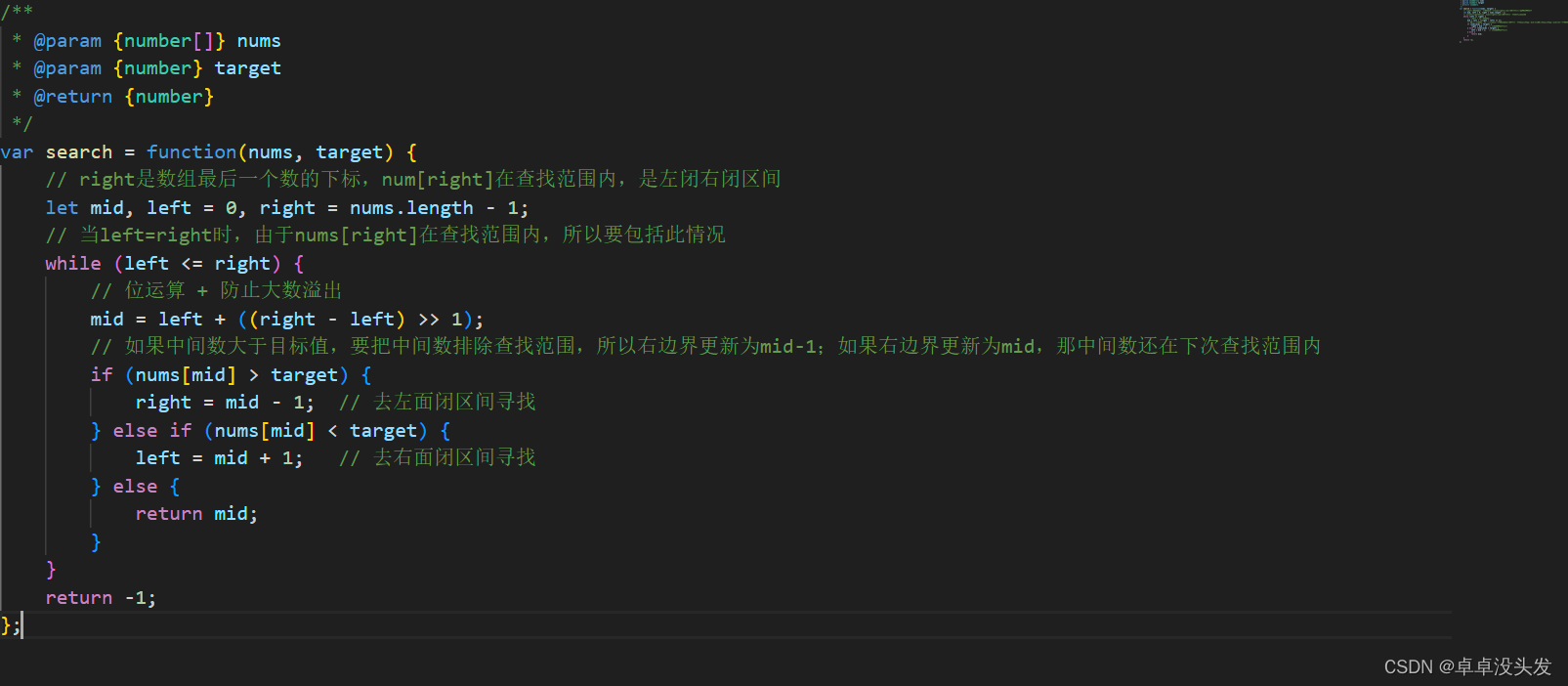
具体实现(以LeeCode 704题为例)
题目:

答案:
你学废了吗
这篇关于关于二分法的理解(以JS为例)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





