本文主要是介绍背包问题----完全背包(最优方案总数分析及实现),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本人博文《背包问题----完全背包(详解|代码实现|背包具体物品的求解)》中已详细谈过完全背包问题,同时在博文《背包问题---01背包最优方案总数(原理剖析代码实现)》中也总结过01背包的最优方案总数的实现。这里我们模仿01背包最优方案总数方法给出完全背包的最优方案求解方法。
重写完全背包的动态规划的状态及状态方程:
完全背包是在N种物品中选取若干件(同一种物品可多次选取)放在空间为V的背包里,每种物品的体积为C1,C2,…,Cn,与之相对应的价值为W1,W2,…,Wn.求解怎么装物品可使背包里物品总价值最大。
设物品种类为N,背包容量为V,每种物品的体积为C[i],价值为W[i]。
子问题定义:F[i][j]表示前i种物品中选取若干件物品放入剩余空间为j的背包中所能得到的最大价值。
状态方程为:
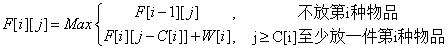 (2-2)
(2-2)
在文章《背包问题---01背包最优方案总数(原理剖析代码实现)》中曾定义G[i][j]代表F[i][j]的方案总数。这里我们也做相同的定义,那么最终的结果应该为G[N][V]。
由01背包转变到完全背包后G[i][j]该怎么求?
对于01背包来说,G[i][j]求法如下(摘自:《背包问题---01背包最优方案总数(原理剖析代码实现)》):
如果F[i][j]=F[i-1][j]且F[i][j]!=F[i-1][j-C[i]]+W[i]说明在状态[i][j]时只有前i-1件物品的放入才会使价值最大,所以第i件物品不放入,那么到状态[i][j]的方案数应该等于[i-1][j]状态的方案数即G[i][j]=G[i-1][j];
如果F[i][j]=F[i-1][j-C[i]]+W[i] 且F[i][j]!=F[i-1][j]说明在状态[i][j]时只有第i件物品的加入才会使总价值最大,那么方案数应该等于[i-1][j-C[i]]的方案数,即G[i][j]=G[i-1][j-C[i]];
如果F[i][j]=F[i-1][j-C[i]]+W[i] 且F[i][j]=F[i-1][j]则说明即可以通过状态[i-1][j]在不加入第i件物品情况下到达状态[i][j],又可以通过状态[i-1][j-C[i]]在加入第i件物品的情况下到达状态[i][j],并且这两种情况都使得价值最大且这两种情况是互斥的,所以方案总数为G[i][j]=G[i-1][j-C[i]]+ G[i-1][j]。
对于完全背包,我们也可以根据其状态方程来进行条件判断:
如果F[i][j] = F[i-1][j]且F[i][j] != F[i][j-C[i]]+W[i],说明背包总不存在第i种物品,也就是说背包种物品仍由前i-1种物品组成,那么应该有G[i][j] = G[i-1][j];
如果F[i][j] = F[i][j-C[i]]+W[i]且F[i][j] != F[i-1][j],则说明背包中必定存在第i种物品使背包达到[i][j]状态的最大值,G[i][j] = G[i]
这篇关于背包问题----完全背包(最优方案总数分析及实现)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







