本文主要是介绍刷题笔记2:用位运算找“只出现一次的一个数”,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. & 和 | 的基本操作
137. 只出现一次的数字 II - 力扣(LeetCode)
先对位运算的操作进行复习:
1、>> 右移操作符
移位规则:⾸先右移运算分两种:1. 逻辑右移:左边⽤0填充,右边丢弃2. 算术右移:左边⽤原该值的符号位填充,右边丢弃一般的编译器都默认使用算术右移。
2. << 左移操作符
移位规则:左边抛弃、右边补0
注意,所有的操作符只能移动整数。
3. & 和 |
& //按位与
| //按位或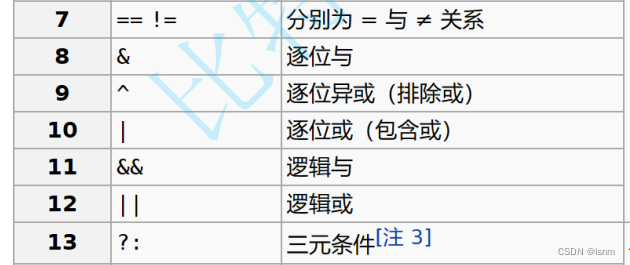
& :
- 清零特定位 (m中特定位置0,其它位为1,s=s&m或s&=m)
- 取某数中指定位 (m中特定位置1,其它位为0,s=s&m或s&=m) 比如 最经典的
for(i=0;i<32;++i) //int是32位二进制整数 int ans =(x>>i)& 1;由于1的补码是 000...0001,x每次右移1位来将每一位分别和0000....0001进行按位与,因此每一轮循环都能将x的一位赋值给ans,让ans依次得到x的每一个二进制位。
| :
多用于将左操作数某些位置1,其它位不变 (m特定位置为1,其余位置为0,希望将s的特定位置改为1,s |= m)
经典:根据特定的条件将ans中的某几位调整为1(将0000..0001中的1一位一位的往前挪)
if(.....) ans |= (1 << i);
有了以上铺垫,我们再学习思路:
由于除了答案,其余每个数字出现三次,所以这三个相同数字为一组中,就有三个一模一样的32为二进制数据(3个1或3个0),我们将第n位上的所有数据加在一起再对3取模,得到的数据就是ans在这一个二进制位上该有的数据。(很多个3和0取出来的模都为0,此时不论ans对应的这一位是1或0,都能被正确赋值)
答案:
int singleNumber(vector<int>& nums) {int ans = 0;for (int i = 0; i < 32; ++i) {int x = 0;for (int j = 0; j < nums.size(); ++j) {x += (nums[j] >> i) & 1;}if (x % 3) {ans |= (1 << i);}}return ans;}2.小试牛刀
136. 只出现一次的数字 - 力扣(LeetCode)
依然是找出只出现一次的数据,不过按位异或就可以了
^ : 双目运算符按位异或,相异位1,相同为0
int singleNumber(vector<int>& nums) {int ans=0;for(auto e:nums){ans^=e;}return ans;}3.位运算 x & -x 来获取x的lowbit(取出二进制下X最低位的1)
假设x为正数(位操作符都只对整数有用),在x变成-x时,除了第一位的符号位变化外,在由原码变到反码再到补码(取反加一)时,取反加一中的 “加一”,一定会加到反码由低到高的第一个0上,而反码所有的0都对应的是原码(正数)的1,(所以反码的第一个0对应的就是原码的第一个1)当反码的第一个0(假定这个0在p位置)被加成1后,就可以通过&运算或得 “最低位在p位置并且是1”的数据。
我们可以认为x &-x是一种取得最低位1的技巧,并且这个用法对负数也凑效。
并且,在y = x & -x后,y是个除了符号位和p位置以外,其余位置都是0的数。
来个大的:
260. 只出现一次的数字 III - 力扣(LeetCode)
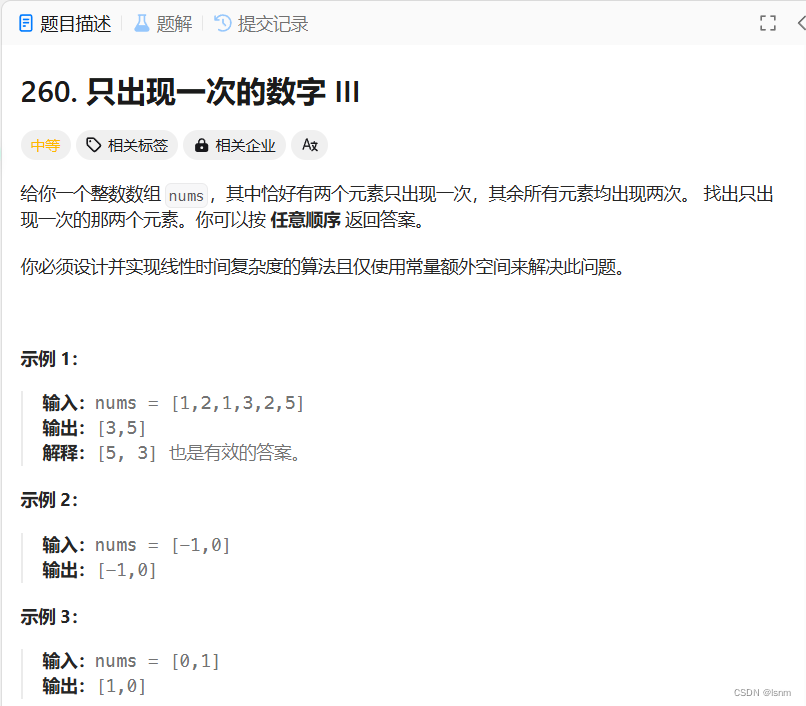
就像刚刚的小试牛刀,我们可以用异或消掉除了ans数组(用于存放两个只出现一次的数a, b)之外的所有数据。不过这两个被异或在一起的数据(x = a^b)该怎么分开呢?
分开的方法:
对于x,x的每一个1,一定都是由一个数的1和另一个数的0组成的。
在这个理论的基础上,我们通过x & -x来获得一个和x的最低位1(假设在位置p)相同,其他(除最高位)都是0的数字y。我们通过 判断位置p是否为1将nums数组分成两组,所以ans数组中的两个数字一定就被分开了,两组中剩下的其他数字一定是成对出现的,将两个组分别全部异或就能得到答案。
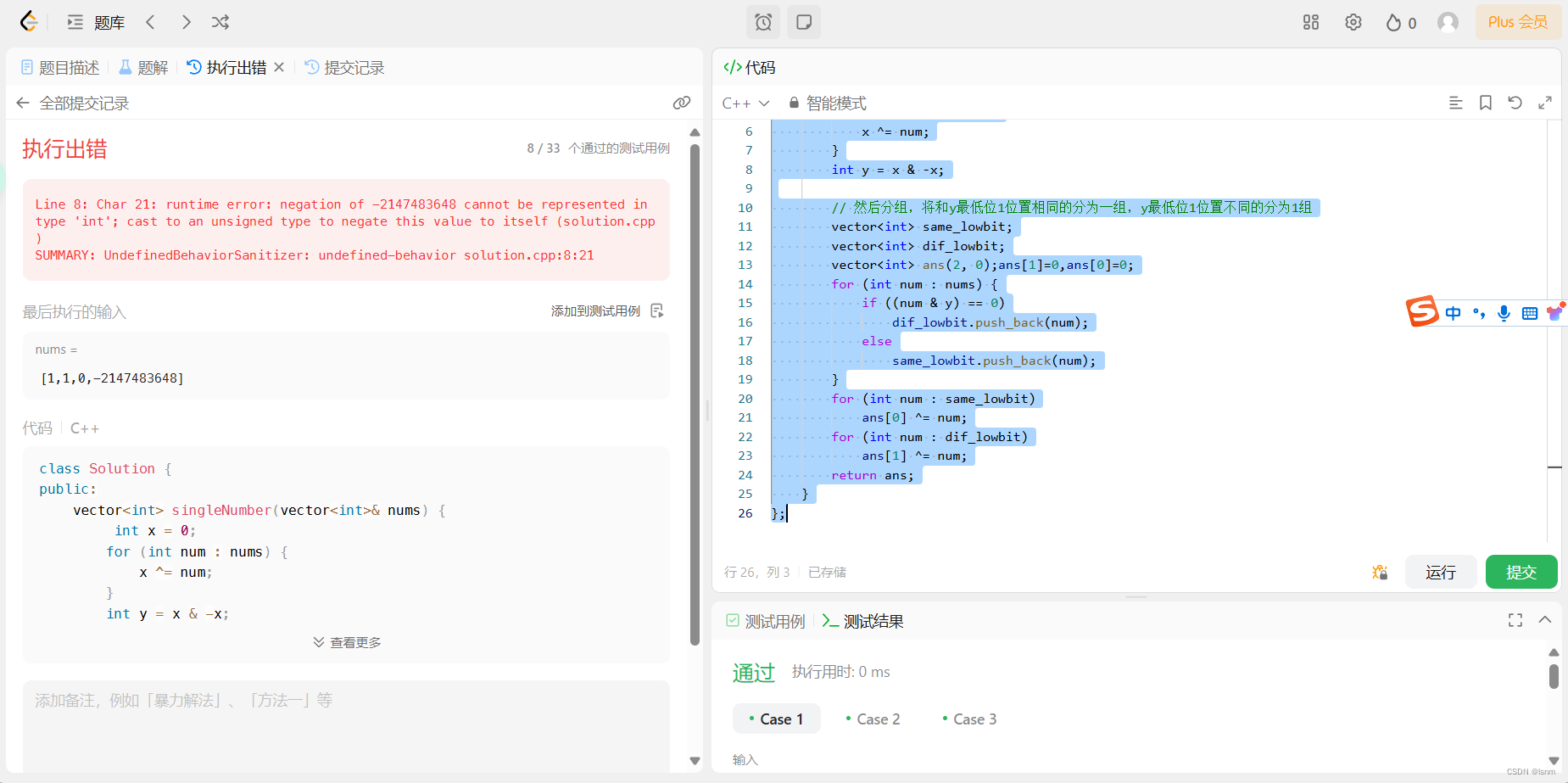
没有全部通过,原因是当测试用例中有x为-2^31时,-x(2^31)没法被放进int
我们处理如下:
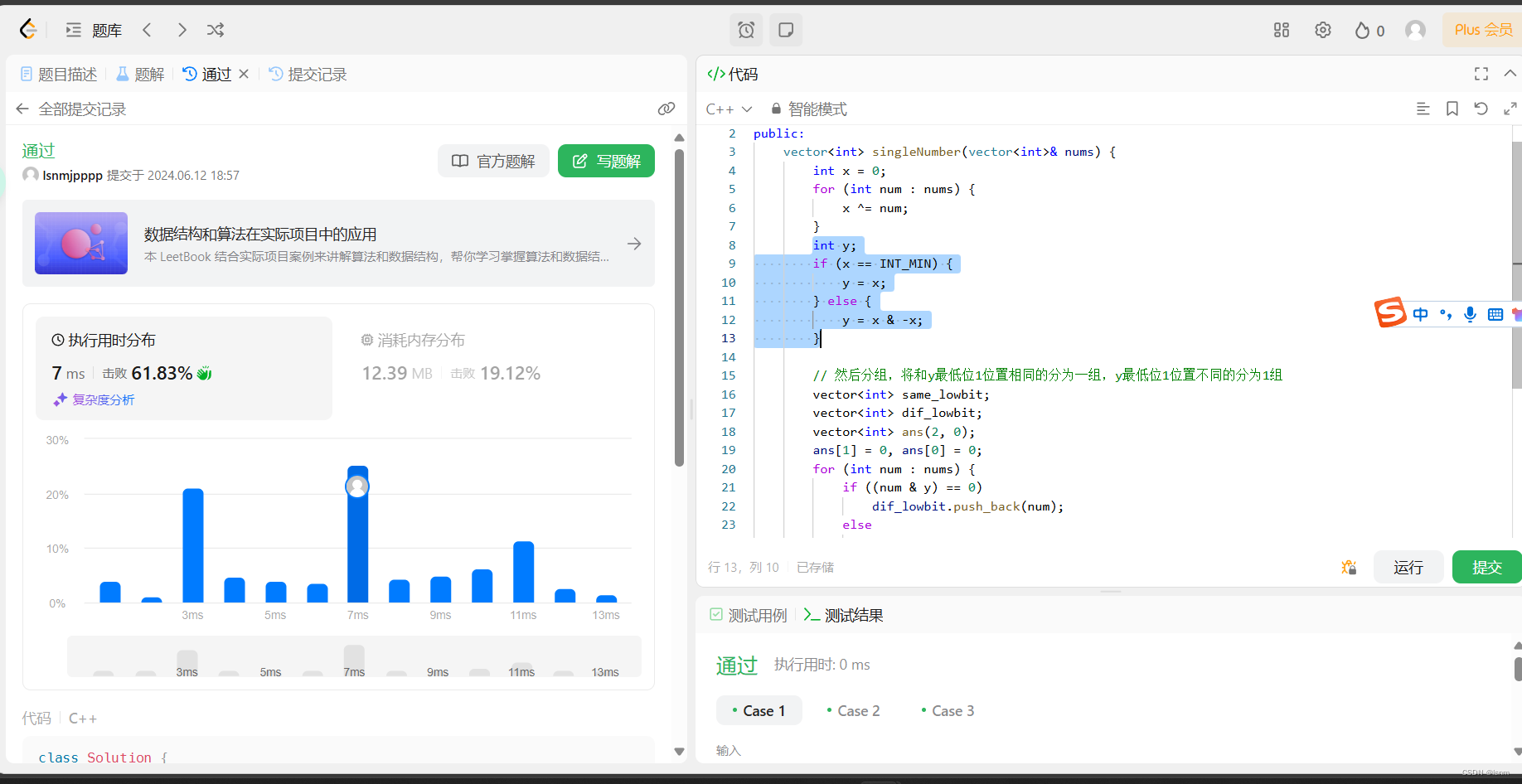
会在x处出现-2^31次方的,答案一定是0和-2^31,否则x不会等于-2^31
并且在下文中,0和-2^31也的确会分开,因此达到目的。
各位都是工科生,仔细想想按位异或的最后一步就明白了。
这篇关于刷题笔记2:用位运算找“只出现一次的一个数”的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





