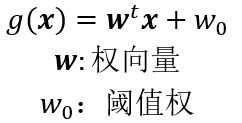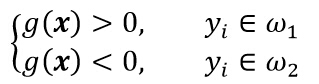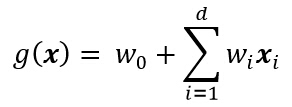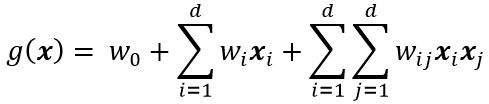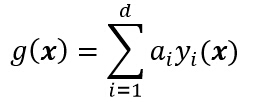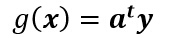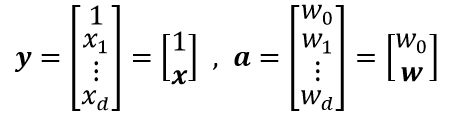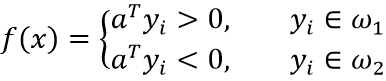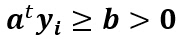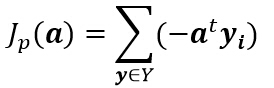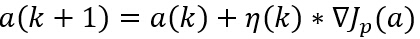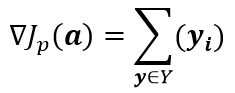本文主要是介绍模式识别六--感知器的实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章转自:http://www.kancloud.cn/digest/prandmethod/102848
在之前的模式识别研究中,判别函数J(.)的参数是已知的,即假设概率密度函数的参数形式已知。本节不考虑概率密度函数的确切形式,使用非参数化的方法来求解判别函数。由于线性判别函数具有许多优良的特性,因此这里我们只考虑以下形式的判别函数:它们或者是x的各个分量的线性函数,或者是关于以x为自变量的某些函数的线性函数。在设计感知器之前,需要明确以下几个基本概念:
一、判别函数:是指由x的各个分量的线性组合而成的函数:
若样本有c类,则存在c个判别函数,对具有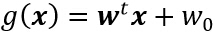
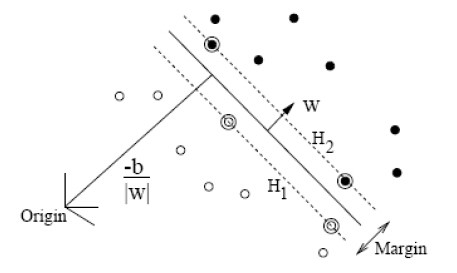
方程g(x)=0定义了一个判定面,它把两个类的点分开来,这个平面被称为超平面,如下图所示。
二、广义线性判别函数
线性判别函数g(x)又可写成以下形式:
其中系数wi是权向量w的分量。通过加入另外的项(w的各对分量之间的乘积),得到二次判别函数:
因为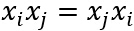
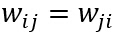
若继续加入更高次的项,就可以得到多项式判别函数,这可看作对某一判别函数g(x)做级数展开,然后取其截尾逼近,此时广义线性判别函数可写成:
或:
这里y通常被成为“增广特征向量”(augmented feature vector),类似的,a被称为“增广权向量”,分别可写成:
这个从d维x空间到d+1维y空间的映射虽然在数学上几乎没有变化,但十分有用。虽然增加了一个常量,但在x空间上的所有样本间距离在变换后保持不变,得到的y向量都在d维的自空间中,也就是x空间本身。通过这种映射,可以将寻找权向量w和权阈值w0的问题简化为寻找一个简单的权向量a。
三、样本线性可分
即在特征空间中可以用一个或多个线性分界面正确无误地分开若干类样本;对于两类样本点w1和w2,其样本点集合表示为: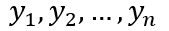
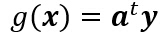
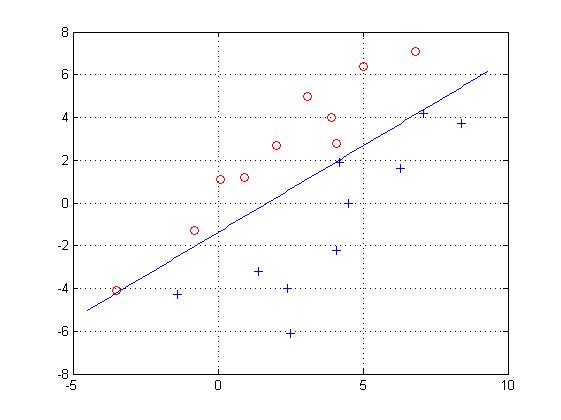
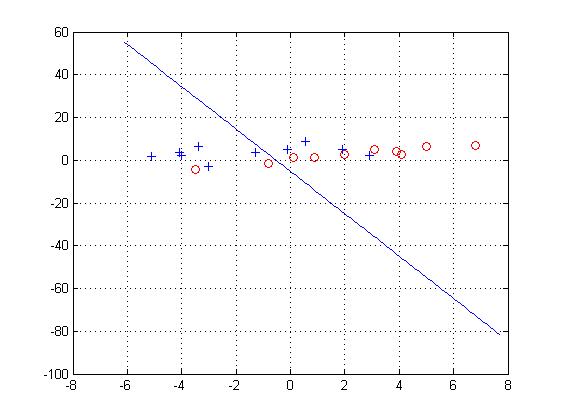
则称样本是线性可分的。如下图中第一个图就是线性可分,而第二个图则不可分。所有满足条件的权向量称为解向量。
通常对解区限制:引入余量b,要求解向量满足:
余量b的加入在一定程度上可防止优化算法收敛到解区的边界。
四、感知器准则函数
这里考虑构造线性不等式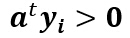
其中Y是被权向量a错分的样本集。当且仅当JP(a) = min JP(a) = 0 时,a是解向量。这就是感知器(Perceptron)准则函数。
1.基本的感知器设计
感知器准则函数的最小化可以使用梯度下降迭代算法求解:
其中,k为迭代次数,η为调整的步长。即下一次迭代的权向量是把当前时刻的权向量向目标函数的负梯度方向调整一个修正量。
即在每一步迭代时把错分的样本按照某个系数叠加到权向量上。这样就得到了感知算法。
2.批处理感知器算法
3.固定增量感知器算法
通常情况,一次将所有错误样本进行修正不是效率最高的做法,更常用是每次只修正一个样本或一批样本的固定增量法:
五、收敛性分析:
只要训练样本集是线性可分的,对于任意的初值 a(1) ,经过有限次迭代运算,算法必定收敛。而当样本线性不可分时,感知器算法无法收敛。
总结:感知器是最简单可以“学习”的机器,是解决线性可分的最基本方法。也是很多复杂算法的基础。感知器的算法的推广有很多种,如带裕量的变增量感知器、批处理裕量松弛算法、单样本裕量松弛算法等等。
以下是批处理感知器算法与固定增量感知器算法实现的MATLAB代码,并给出四组数据以供测试:
% 批处理感知器算法
function BatchPerceptron(w1, w2)figure;
plot(w1(:,1),w1(:,2),'ro');
hold on;
grid on;
plot(w2(:,1),w2(:,2),'b+');% 对所有训练样本求增广特征向量y
one = ones(10,1);
y1 = [one w1];
y2 = [one w2];
w12 = [y1; -y2]; % 增广样本规范化
y = zeros(size(w12,1),1); % 错分样本集y初始为零矩阵
% 初始化参数
a = [0 0 0]; % [0 0 0];
Eta = 1;
time = 0; % 收敛步数
while any(y<=0)for i=1:size(y,1)y(i) = a * w12(i,:)';end;a = a + sum(w12(find(y<=0),:));%修正向量atime = time + 1;%收敛步数if (time >= 300)break;end
end;
if (time >= 300)disp('目标函数在规定的最大迭代次数内无法收敛');disp(['批处理感知器算法的解矢量a为: ',num2str(a)]);
else
disp(['批处理感知器算法收敛时解矢量a为: ',num2str(a)]);
disp(['批处理感知器算法收敛步数k为: ',num2str(time)]);
end%找到样本在坐标中的集中区域,以便于打印样本坐标图
xmin = min(min(w1(:,1)),min(w2(:,1)));
xmax = max(max(w1(:,1)),max(w2(:,1)));
xindex = xmin-1:(xmax-xmin)/100:xmax+1;
yindex = -a(2)*xindex/a(3)-a(1)/a(3);
plot(xindex,yindex);
title('批处理感知器算法实现两类数据的分类');% 固定增量感知器算法
function FixedIncrementPerceptron(w1, w2)[n, d] = size(w1);
figure;
plot(w1(:,1),w1(:,2),'ro');
hold on;
grid on;
plot(w2(:,1),w2(:,2),'b+');% 对所有训练样本求增广特征向量y
one = ones(10,1);
y1 = [one w1];
y2 = [one w2];
w12 = [y1; -y2]; % 增广样本规范化
y = zeros(size(w12,1),1); % 错分样本集y初始为零矩阵
% 初始化参数
a = [0 0 0];
Eta = 1;
% k = 0;
time = 0; % 收敛的步数
yk = zeros(10,3);y = a * w12';
while sum(y<=0)>0
% for i=1:size(y,1)
% y(i) = a * w12(i,:)';
% end;y = a * w12';rej=[];for i=1:2*n %这个循环计算a(K+1) = a(k) + sum {yj被错误分类} y(j)if y(i)<=0a = a + w12(i,:);rej = [rej i];endend% fprintf('after iter %d, a = %g, %g\n', time, a);% rejtime = time + 1;if ((size(rej) == 0) | (time >= 300))break;end
end;
if (time >= 300)disp('目标函数在规定的最大迭代次数内无法收敛');disp(['固定增量感知器算法的解矢量a为: ',num2str(a)]);
else
disp(['固定增量感知器算法收敛时解矢量a为: ',num2str(a)]);
disp(['固定增量感知器算法收敛步数kt为: ',num2str(time)]);
end
%找到样本在坐标中的集中区域,以便于打印样本坐标图
xmin = min(min(w1(:,1)),min(w2(:,1)));
xmax = max(max(w1(:,1)),max(w2(:,1)));
xindex = xmin-1:(xmax-xmin)/100:xmax+1;
% yindex = -a(2)*xindex/a(3)-a(1)/a(3);
yindex = -a(2)*xindex/a(3) - a(1)/a(3);
plot(xindex,yindex);
title('固定增量感知器算法实现两类数据的分类');close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 感知器实验
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%w1 = [ 0.1 1.1;...6.8 7.1;...-3.5 -4.1;...2.0 2.7;...4.1 2.8;...3.1 5.0;...-0.8 -1.3;...0.9 1.2;...5.0 6.4;...3.9 4.0];w2 = [ 7.1 4.2;...-1.4 -4.3;...4.5 0.0;...6.3 1.6;...4.2 1.9;...1.4 -3.2;...2.4 -4.0;...2.5 -6.1;...8.4 3.7;...4.1 -2.2];w3 = [-3.0 -2.9;...0.54 8.7;...2.9 2.1;...-0.1 5.2;...-4.0 2.2;...-1.3 3.7;...-3.4 6.2;...-4.1 3.4;...-5.1 1.6;...1.9 5.1];w4 = [-2.0 -8.4;...-8.9 0.2;...-4.2 -7.7;...-8.5 -3.2;...-6.7 -4.0;...-0.5 -9.2;...-5.3 -6.7;...-8.7 -6.4;...-7.1 -9.7;...-8.0 -6.3];BatchPerceptron(w1, w2);FixedIncrementPerceptron(w1, w3);这篇关于模式识别六--感知器的实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!