本文主要是介绍网络空间安全数学基础·期末复习,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、整除与同余
1.最大公因子性质:
(a,b)=(-a,b)=(a,-b)=(-a,-b)=(|a|,|b|)
(0,a)=a
2.最大公因子求解(欧几里得算法、辗转相除法)
例:(-3824,1837)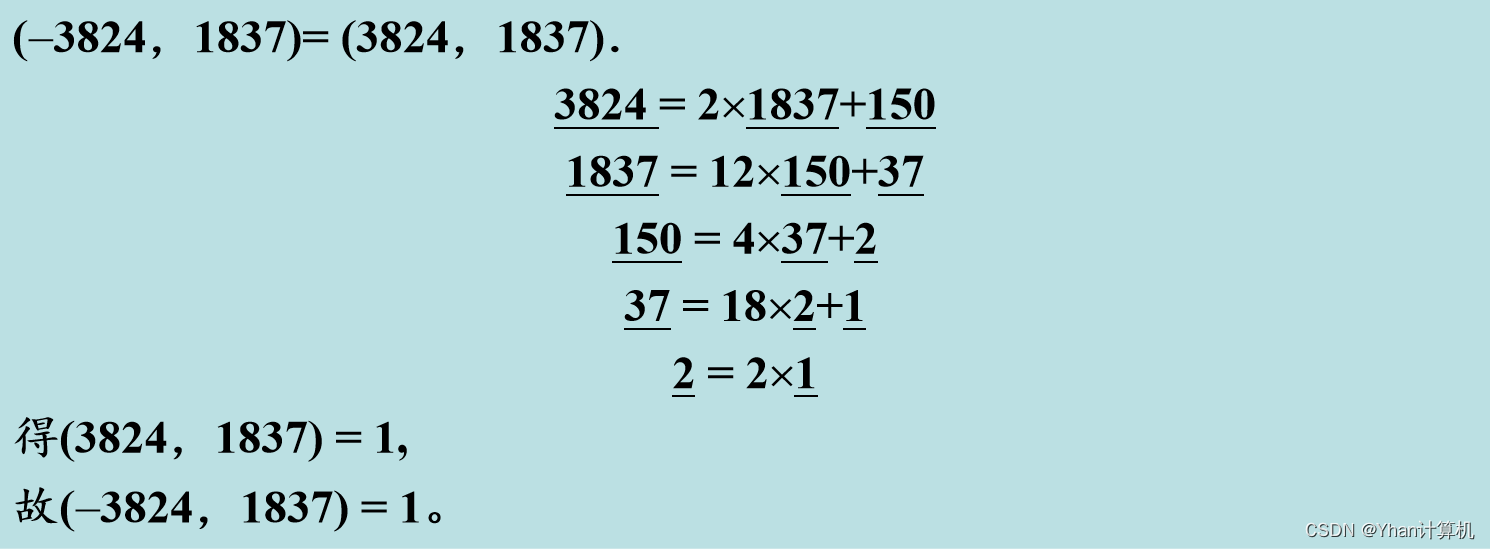
3.最大公因子定理:
设a,b是两个不全为零的整数,则存在两个整数u, v,使得:(a, b)=ua+vb。
例:将a = 888,b = 312的最大公因子表示为(a,b) = ua+vb。
4.最小公倍数性质:
[a,b] = [–a,b] = [a,–b] = [–a,–b] = [|a|,|b|]![]() ,特别地,如果(a, b) = 1, [a, b] = |ab|。
,特别地,如果(a, b) = 1, [a, b] = |ab|。
5.算术基本定理:
定理:每个大于1的整数a都可以分解为有限个素数的乘积:a=p1p2…pr。该分解除素数因子的排列外是唯一的。
6.标准因子分解式:
由于p1,p2,…,pr中可能存在重复,所以a的分解式可表示为有限个素数的幂的乘积:![]() ,这称为a的标准因子分解式。
,这称为a的标准因子分解式。
7.Eratosthenes筛法:
设a是任意大于1的整数,则a的除1外最小正因子q是一素数,并且当a是一合数时,![]() 。
。
例:
求不超过100的全部素数。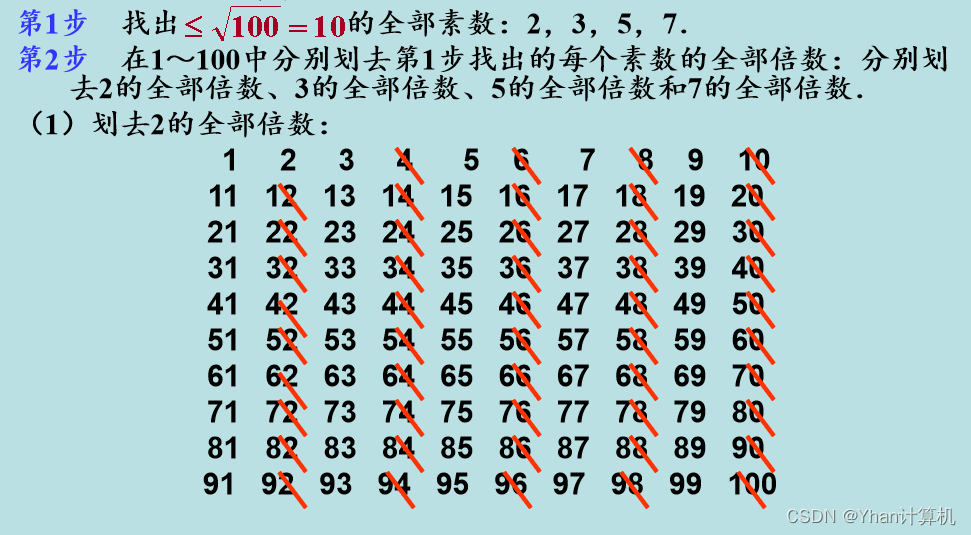

同理可以将因子5,7的倍数划去: (3) 划去5的全部倍数: (4) 划去7的全部倍数。
最终经过上述步骤后剩下的数除1外就是不超过100的全部素 数: (25个) 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
8.快速指数算法
例:求解 2^64 (mod 641)
二、群
★1.群的定义:
设G是一非空集合。如果在G上定义了一个代数运算,称为乘法,记为ab,而且这个运算满足下列条件,那么(G,·)称为一个群:
1) G对于乘法是封闭,即对于G中任意元素a,b,有ab∈G;(封闭性)
2) 对于G中任意元素a,b,c,有(ab)c = a(bc) ;(交换律)
(满足上述两点则为半群)
3) 在G中有一个元素e,对于G中任意元素a,有 ea=a;(左单位元)
4) 对于G中任一元素a都存在G中的一个元素b,使ba=e。(左逆元)
注意:
1) 左单位元也是右单位元,左逆元也是右逆元,所以单位元和逆元不再区分左右。
2) 单位元和逆元是唯一的。
3) 如果一个非空有限集合G中的运算封闭且满足结合律(半群),则它是一个群的充分必要条件是满足消去律(如果ax=ax’,则x=x’;(左消去) 如果ya=y’a,则y=y’。 (右消去))。
2.群的阶
如果一个群G中元素的个数是无限多个,则称G是无限群;如果G中的元素个数是有限多个,则称G是有限群,G中元素的个数称为群的阶,记为|G|。
3.子群
一个群G的一个子集H如果对于G的乘法构成一个群, 则称H为G的子群,记作H≤G。一个群G至少有两个子群:G本身;只包含单位元的子集{e}, 它们称为G的平凡子群,其他子群成为真子群(H<G)。
注意:
1) 子群与群单位元同一。
2) a∈H,a^(-1)是a在G中的逆元,则a^(-1)∈H。
4.子群判定:
一个群G的一个非空子集H构成一个子群的充分必要条件是:对于∀a,b∈H,有:ab^(-1)∈H。
一个群G的一个非空有限子集H构成一个子群的充分必要条件是:对于任意a,b∈H,有ab∈H。
5.同构与同态
1) 映射
单射:∀a, b∈A,如果a≠b,则 f(a)≠f(b)。
满射:∀b∈B,总有a∈A,使f(a)=b。
一一映射:既是满射又是单射的映射。
2) 同态与同构
假设G和G’是两个群,若存在映射f:G→G’ 满足:∀a, b∈G,均有 f(a·b)= f(a)⊙f(b)则称f是G到G’的一个同态映射或简称同态。
如果f是单射,则称f是单同态;
如果f是满射,则称f是满同态;
如果f是一一映射,则称f是同构映射;
如果G=G’,同态f称为自同态,同构映射f称为自同构映射。
3) 反像
设f是G到G’的同态映射。∀a’∈G’,集合 {a|f(a)=a’, a∈G}可能是空集,也可能包含一个以上的元素(f不是单射)。这个集合称为a’的完全反像。(可以类比函数值y所对应的x值,但并不完全一样,因为一个x仅能对应一个y,而此处一个a’可以有多个a对应,如下图)
特别地,单位元的完全反像称为同态映射f的核,记为ker(f),即ker(f) = {a|a∈G,f(a)=e’},ker(f)是G的子群,称为f的核子群。
这篇关于网络空间安全数学基础·期末复习的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






