秋招突击——6/10——复习{（树形DP）树的最长路径、}——新作{电话号码的字母组合}

本文主要是介绍秋招突击——6/10——复习{（树形DP）树的最长路径、}——新作{电话号码的字母组合}，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

引言

• 中间面试了两天，去上海呆了一天，在女朋友这里，休息了三天。

复习

树形DP——树的最长路径

思路分析

• 这个可以想象成迷宫的寻路问题，然后总共有n-1条路径，最差的情况遍历n！的次数人，然后找到最优解，时间复杂度太高了。
• 这样想可真的是太幼稚了，应该直接暴力枚举每一个点到其他店的最长的边，时间复杂度也就是O(n2)
• 使用动态规划，找到状态表示？可以尝试一下，f【i】表示所有能够到达节点i的所有路径中的最长的值，但是不存在环路的问题，并且走过的节点不能再走一遍，我是不是应该保存对应的状态变化过程？
• 我觉得可以先使用之前类似迷宫的动态规划思路，然后再增加一个回路检测的功能。
• 在简化一下，遍历起点和终点，然后进行搜索。
• 感觉不对，参考一下克鲁斯卡尔算法，但是实现起来没什么头绪

参考思路

求图的最长的直径的通用方法

• 任取一点作为起点，找到距离该点最远的一个点u，使用BFS或者DFS进行搜搜
• 再找到距离u最远的一个点v，同样是使用DFS或者BFS
• 那么u和v之间的路径就是一条直径。

证明

• 首先证明任取一个点u，u一定是某一个直径的一条端点，然后从u求出来的某一个最长的边是直径
• 情况一，两个边之间没有任何的交点，可以使用反证法进行证明。
  
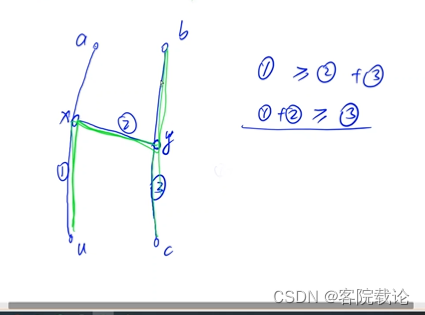
• 情况二，两者之间存在交点
  • 那么现在，有一个问题，就是比一个直径长的边，一定是直径吗？
    
• 通过上述证明，u一定是某一个直径的端点，然后在开始从u出发，找到对应节点v，uv就是对应的路径。

树形DP分析方法

• 想办法把所有路径都枚举一边，然后找到边权和最大的边。集合分类的依据是什么？
  • 每条直径都有一个最高的点，然后找到挂到这个点上的所有路径的长度的最大值
  • 这里分类的依据就是，所有路径上最高的点是该点的路径集合中的权重之和的最大值
    • 这里还是很巧妙的，我每一次就不需要进行BFS或者DFS，只需要找当前的子节点的作为最高节点的路径

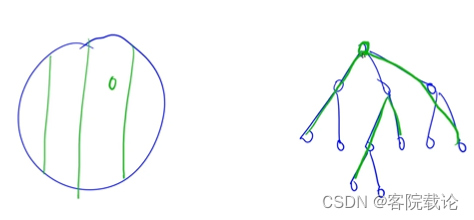
• 以每一个点的为起点，然后计算以当前点为起点的所有路径中的最大值和次大值，然后累加和就是最大值。
• 还有一种情况就是，直接一个点到底，仅仅取最大值就行了

问题

• 虽然通过固定节点，对所有路径进行集合划分，但是有一个问题，如何定义最高的节点？以及如何确保没有回路的情况？
• 这里的代码属实没有看懂，有以下几个问题
  • 使用若干个一维数组表示树形结构
  • 创建father参数方式回传。

参考代码

• 这里还是没有看懂，时间不够了，花了很多时间，都不行

#include <iostream>
#include <cstring>using namespace std;const int N = 1e4 + 10, M = N << 1; //初始不确定树的拓扑结构，因此要建立双向边int n;
int h[N], e[M], w[M], ne[M], idx;
int f1[N], f2[N], res;void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int father)
{f1[u] = f2[u] = 0;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == father) continue;dfs(j, u);if (f1[j] + w[i] >= f1[u]) f2[u] = f1[u] ,f1[u] = f1[j] + w[i]; //最长路转移 else if (f1[j] + w[i] > f2[u]) f2[u] = f1[j] + w[i];            //次长路转移}res = max(res, f1[u] + f2[u]);
}
int main()
{memset(h, -1, sizeof h);scanf("%d", &n);for (int i = 0; i < n - 1; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}dfs(1, -1); //我们可以任意选取一个点作为根节点，这样整棵树的拓扑结构被唯一确定下来了printf("%d\n", res);return 0;
}

作者：一只野生彩色铅笔
链接：https://www.acwing.com/solution/content/63883/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

• 这里先一步一步来吧，先解决树形数据的存储问题。

使用一维数组模拟邻接表存储树形结构或者稀疏图

• h【n】：存储每一个节点的第一条边的索引
• e【M】：存储边的终点
• w【M】：存储每条边的权重
• ne【M】：存储每条边下一条边的索引
• idx：边的索引指针，初始值为0，用来记录边的数量

下述为添加边的具体代码

void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

• idx：是边的序号，因为这里是按照边的顺序添加边的
• e[idx] = b：第idx边的终点是b
• w[idx] = c：第idx边的权重是c
• ne[idx] = h[a]：h【a】暂时还没有更新还是上一个邻接边的序号idx，所以，这里记录一下，当前邻接边的下一个边的序号是当前节点为起点的上一个临界边的序号
• h[a] = idx++：记录一下，以a为起点，最新输入的边的索引，具体流程图应该如下

新作

电话号码的组合

题目链接

思路分析

• 这里最多四个字符，然后每一个字符都表示三到四个字母，直接暴力搜索完全没有任何问题。
• 实际上就三种情况，如果不追求代码的美观性，就多写几段，这里是想着用三层循环来写，然后增加美观性，写得太久了，没时间测试了。直接看源码。

vector<string> letterCombinations(string d) {unordered_map<char,string> s = {{'2',"abc"},{'3',"def"},{'4',"ghi"},{'5',"jkl"},{'6',"mno"},{'7',"pqrs"},{'8',"tuv"},{'9',"wxyz"},};vector<string> res,temp;// 给你一个字符串，然后遍历其中的每一个元素，往其中添加元素for (int i = 1; i <= d.size(); ++i) {for (int j = 0; j < s[d[i - 1]].size(); ++j) {// 判定是否为空的情况if (res.size() <= s[d[i - 1]].size()){string t;temp.emplace_back(t+=s[d[i - 1]][j]);}elsefor (auto x : res) {x +=  s[d[i - 1]][j];temp.push_back(x);}res = temp;}}

参考实现

• 这里直接使用回溯实现，我应该多去想想看的，而且这里也没有使用很多的数据机构，使用的string数组实现，效果会更好。有很多技巧，需要我后续不断加深巩固学习。
• 使用string表示映射

string strs[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"
};

• 将char转成数字

 for(auto c:strs[digits[u] - '0']){dfs(digits, u + 1,path + c); }

• 最终实现结果
  

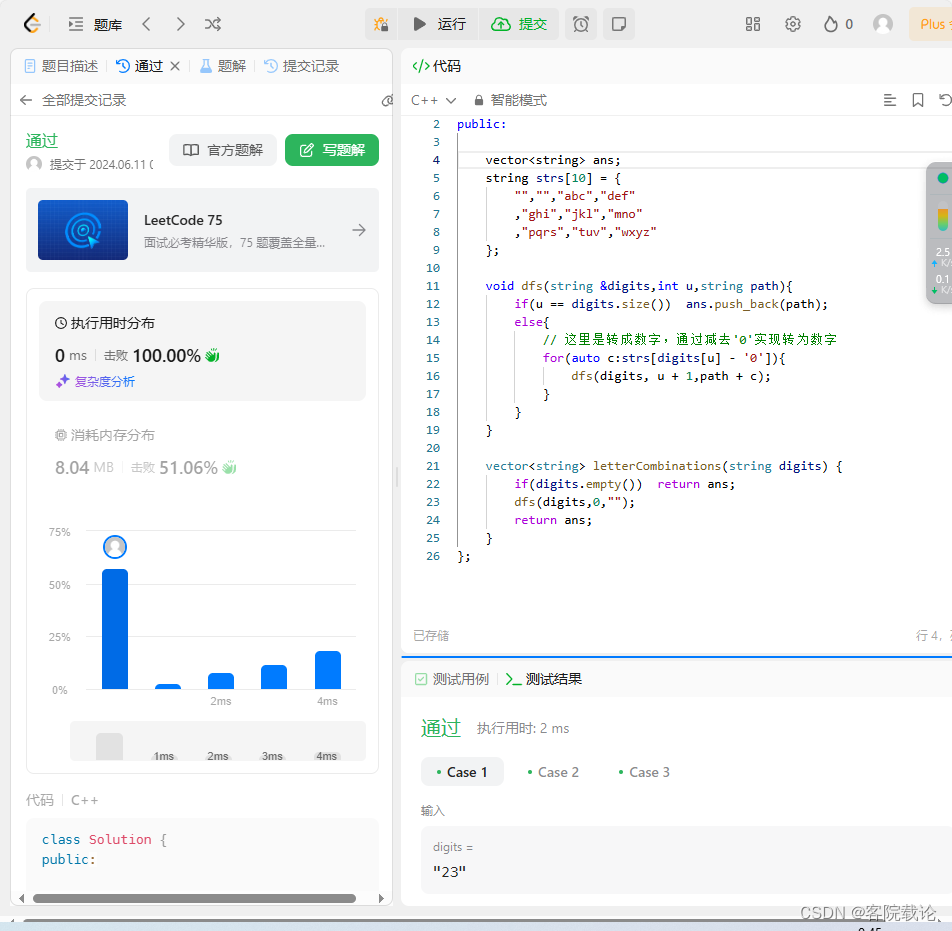
总结

• 今天无论是新学的题目，还是复习的题目，都做得蛮差的，好好练习一下，后续总归会有进展的，加油
• 今天学到了很多技巧。

这篇关于秋招突击——6/10——复习{（树形DP）树的最长路径、}——新作{电话号码的字母组合}的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---