【数据结构（邓俊辉）学习笔记】图07——最短路径

本文主要是介绍【数据结构（邓俊辉）学习笔记】图07——最短路径，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. 概述

学习下最短路径和Dijistra算法

1. 问题

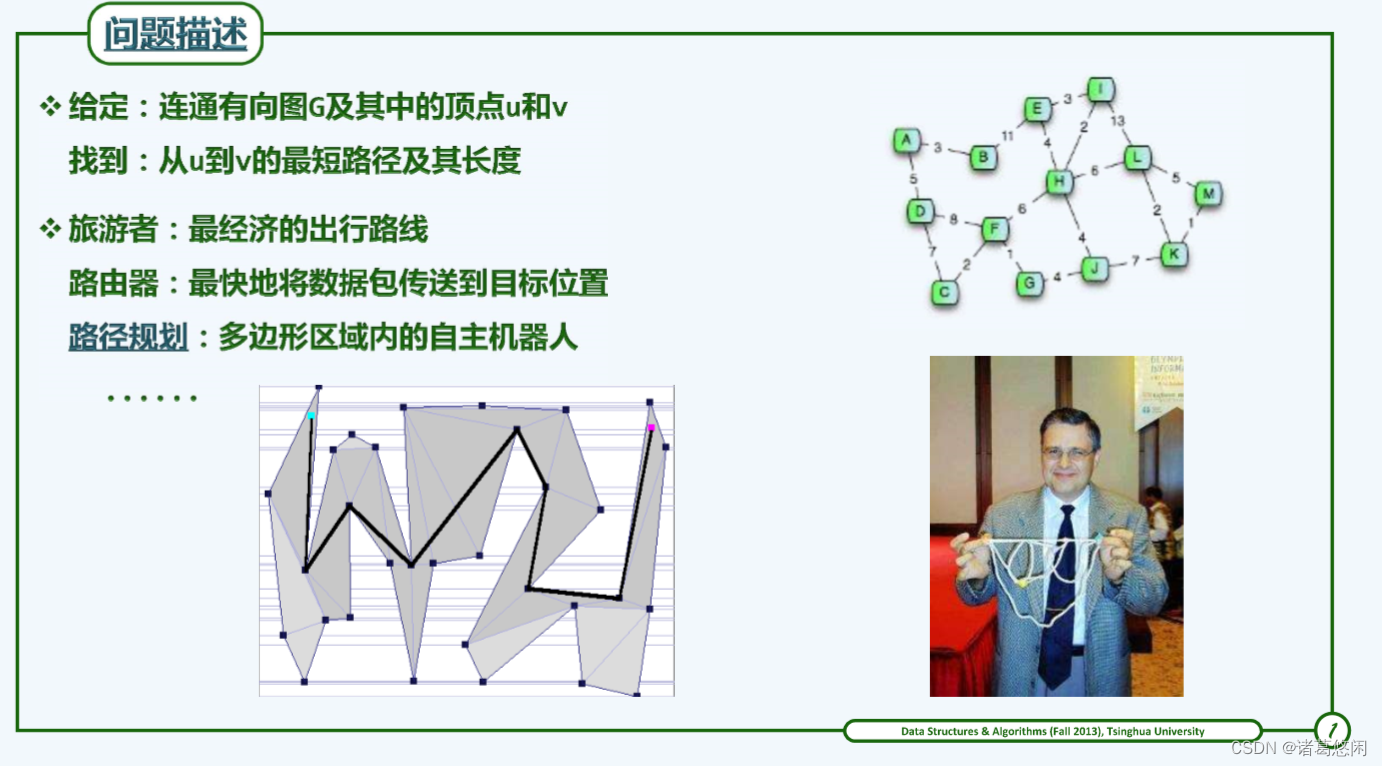
给定带权网络G = (V, E)，以及源点（source）s ∈ V，对于所有的其它顶点v，s到v的最短通路有多长？该通路由哪些边构成？

2. 最短路径

2.1 最短路径树

2.1.1 单调性

设顶点s到v的最短路径为$\rho$。于是对于该路径上的任一顶点u，若其在$\rho$上对应的前缀为$\sigma$，则$\sigma$也必
是s到u的最短路径（之一）。

2.1.2 歧义性

较之最小支撑树，最短路径的歧义性更难处理。首先，即便各边权重互异，从s到v的最短路径也未必唯一。另外，当存在非正权重的边，并导致某个环路的总权值非正时，最短路径甚至无从定义。因此以下不妨假定，带权网络G内各边权重均大于零。

2.1. 3 无环性

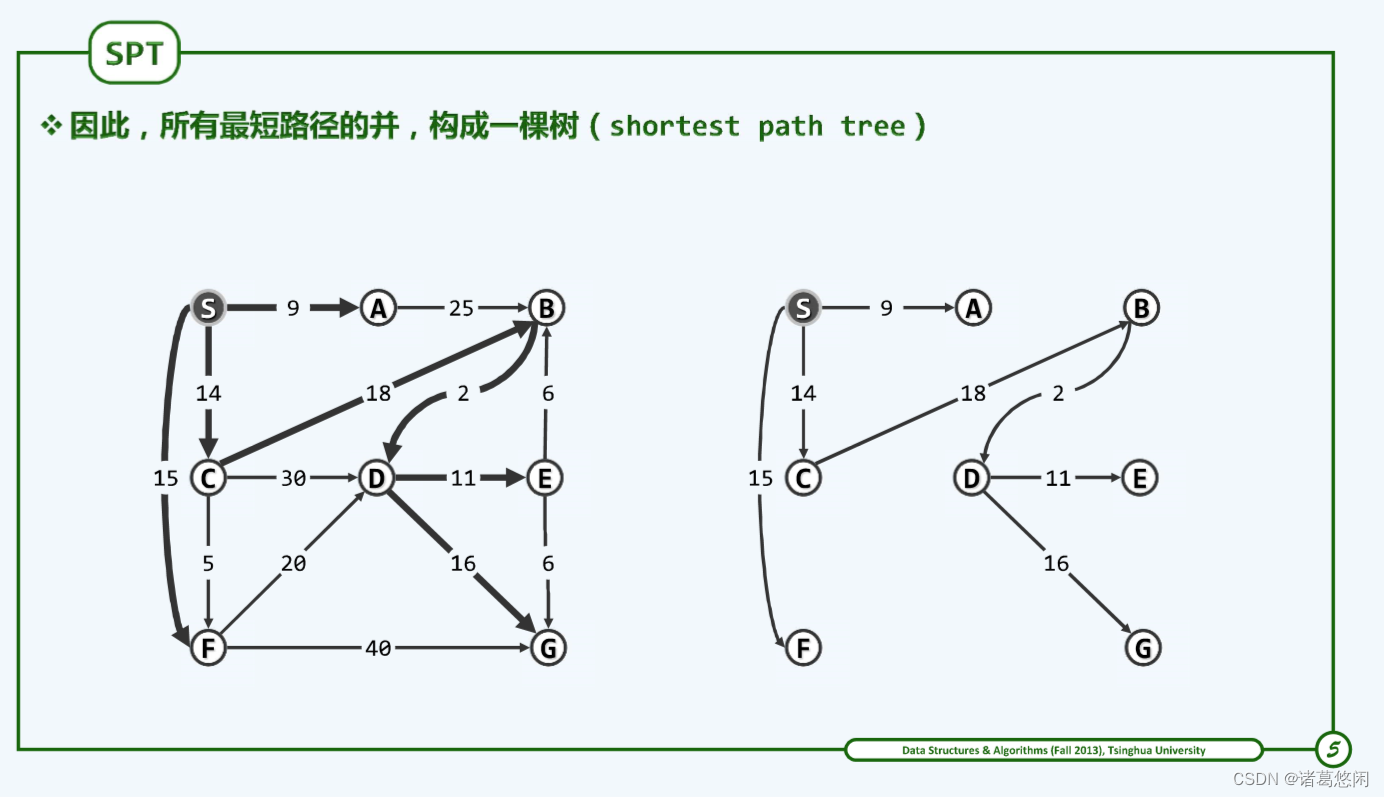考查从源点到其余顶点的最短路径（若有多条，任选其一）。于是由以上单调性，这些路径的并集必然不含任何（有向）回路。这就意味着，如图所示，构成所谓的最短路径树（shortest-path tree）。

2.2 Dijkstra 算法

2.2.1 贪心迭代

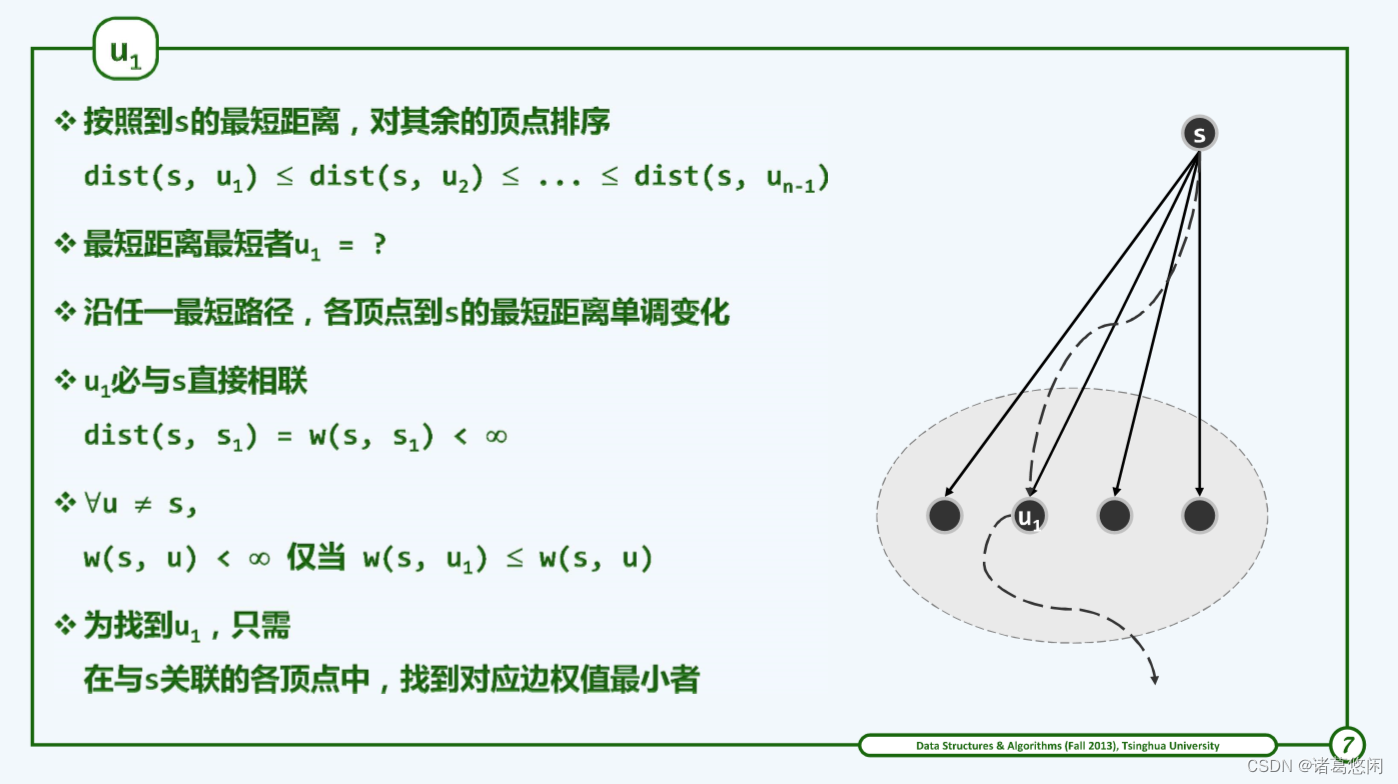
上述思路可知，只要能够确定$u_{k+1}$，便可反过来将$T_k$扩展为$T_{k+1}$。如此，便可按照到s距离的非降次序，逐一确定各个顶点{$u_1$, $u_2$, …, $u_n$}，同时得到各棵最短路径子树，并得到最终的最短路径树T = $T_n$。现在，问题的关键就在于：
~~~~~~~~~~~~~~~~~~                   如何才能高效地找到$u_{k+1}$？
实际上，由最短路径子树序列的上述性质，每一个顶点$u_{k+1}$都是在$T_k$之外，距离s最近者。若将此距离作为各顶点的优先级数，则与最小支撑树的Prim算法类似，每次将$u_{k+1}$加入$T_k$并将其拓展至$T_{k+1}$后，需要且只需要更新那些仍在$T_{k+1}$之外，且与$T_{k+1}$关联的顶点的优先级数。

可见，该算法与Prim算法仅有一处差异：考虑的是$u_{k+1}$到s的距离，而不再是其到$T_k$的距离。

2.2.2 实现

与Prim算法一样，Dijkstra算法也可纳入此前的优先级搜索算法框架。

为此，每次由$T_k$扩展至$T_{k+1}$时，可将$V_k$之外各顶点u到$V_k$的距离看作u的优先级数（若u与$V_k$内顶点均无联边，则优先级数设为+∞）。如此，每一最短跨越边$e_k$所对应的顶点$u_k$，都会因拥有最小的优先级数（或等价地，最高的优先级）而被选中。

唯一需要专门处理的是，在$u_k$和$e_k$加入$T_k$之后，应如何快速地更新$V_{k+1}$以外顶点的优先级数。实际上，只有与$u_k$邻接的那些顶点，才有可能在此后降低优先级数。因此与Prim算法一样，也可遍历$u_k$的每一个邻居v，只要边$u_{k}v$的权重加上$u_k$的优先级数，小于v当前的优先级数，即可将后者更新为前者。

2.2.3 实例

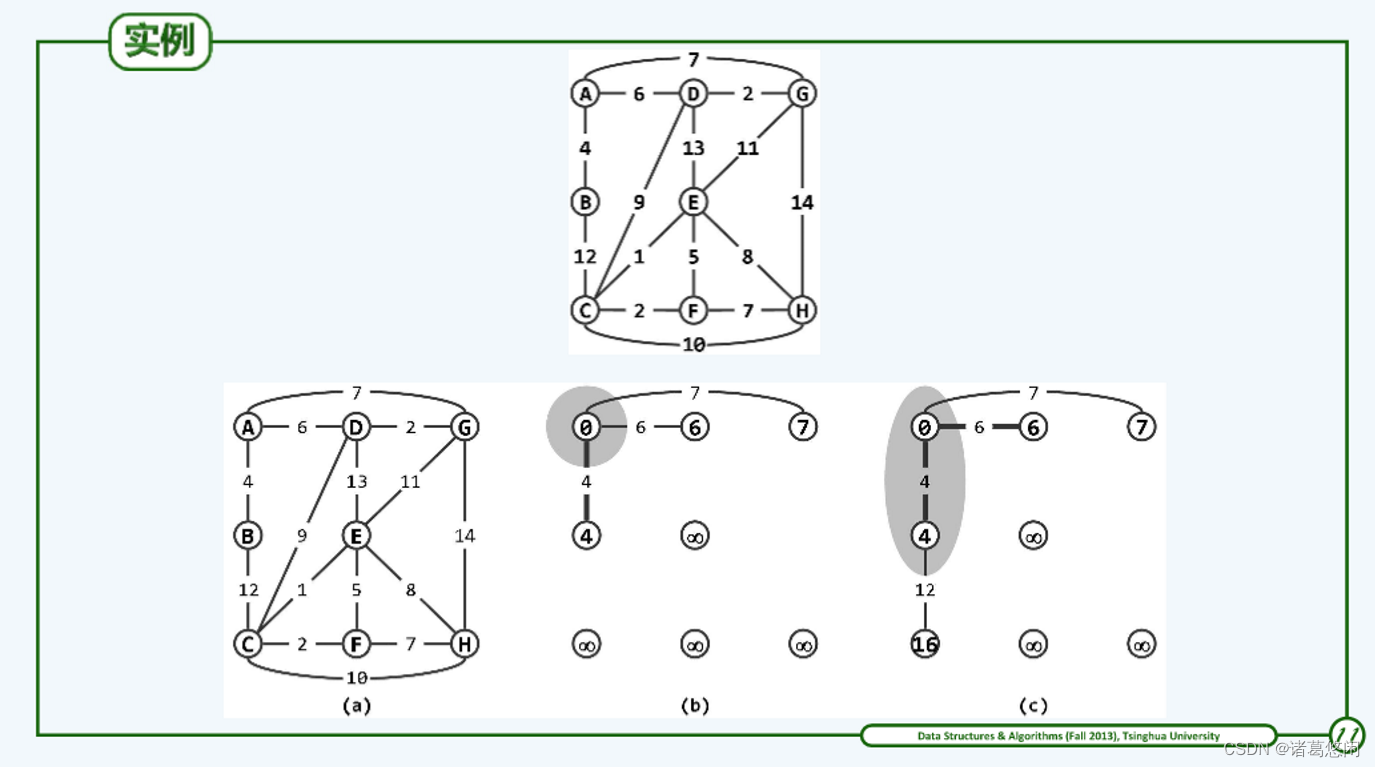
2.2.4 复杂度

不难看出，以上顶点优先级更新器只需常数运行时间。同样根据对PFS搜索性能的分析结论，Dijkstra算法这一实现版本的时间复杂度为O($n^2$)。

作为PFS搜索的特例，Dijkstra算法的效率也可借助优先级队列进一步提高。

这篇关于【数据结构（邓俊辉）学习笔记】图07——最短路径的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---