本文主要是介绍【学术小白成长之路】03三方演化博弈(基于复制动态方程)均衡点与稳定性分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
从本专栏开始,笔者正式研究演化博弈分析,其中涉及到双方演化博弈分析,三方演化博弈分析,复杂网络博弈分析等等。
先阅读了大量相关的博弈分析的文献,总结了现有的研究常用的研究流程,针对每个流程进行拆解。具体学习每个步骤中的步骤的实现方法和流程。基础性文章,希望对您有帮助,如果存在错误或不足之处,还请海涵。且看且珍惜!
文章目录
- 1.均衡点计算
- 2.稳定性分析
- 3.MatLAB的代码实现
1.均衡点计算
参与主体根据既得利益不断调整策略以追求自身利益的改善,最终达到动态平衡的策略称为演化稳定策略(ESS)。
在判定演化稳定策略之前首先要求出演化博弈的均衡点。令F(x))=0、F(y)=0和F(z)=0,即系统策略选择的变化率为零时,可以得到该动力系统的均衡点。
在计算出均衡点之前,我们可以先构建出来雅可比矩阵,先不进行计算,用于后面将均衡点带入雅可比矩阵之中进行计算。
可以看出,雅可比矩阵就对应函数在x,y,z概率上的偏导。

如某篇文章中所示,在计算出复制动态方程后,通过构建的复制动态方程,来构建雅克比矩阵。

这时候,我们令F(x)=0;F (y)=0;F (z)=0就可以计算出对应的xyz的组合,如(0,0,0)、(0,1,0)这样的组合均衡点。
一般会解出来很多这样的组合解,但是这样均衡点不一定具有稳定,还需要进一步计算。
2.稳定性分析
获取均衡点之后,就可以用到上文构建的雅可比矩阵
将求得的均衡点代入雅可比矩阵求此时矩阵对应的特征值
依据特征值,来判断均衡点的稳定性,一般文章中都是以特征值全负值的数为ESS点
如果特征值均小于0,则均衡点有渐进稳定性,为演化稳定策略;
若的特征值均大于0,则为不稳定点;
若特征值有1或2个大大0,则为鞍点:
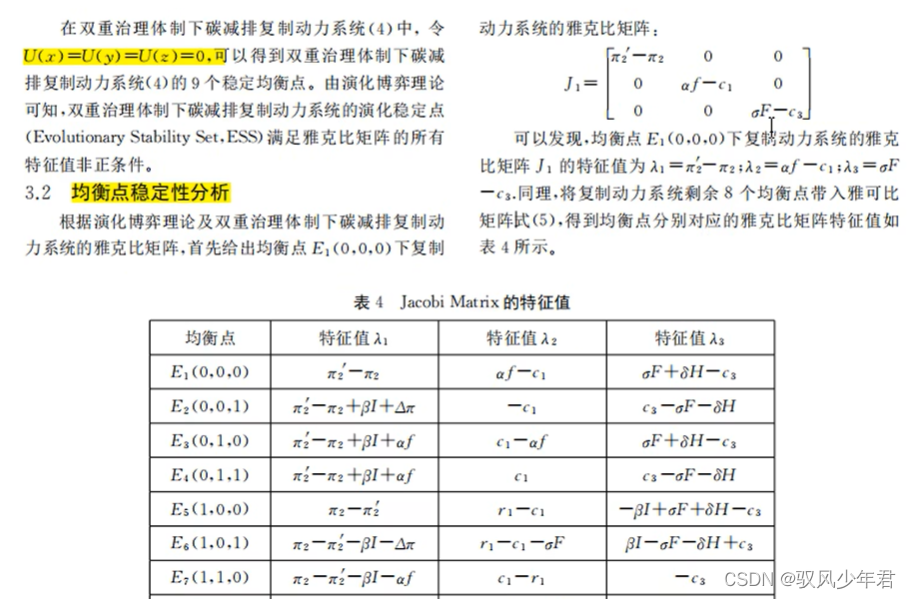
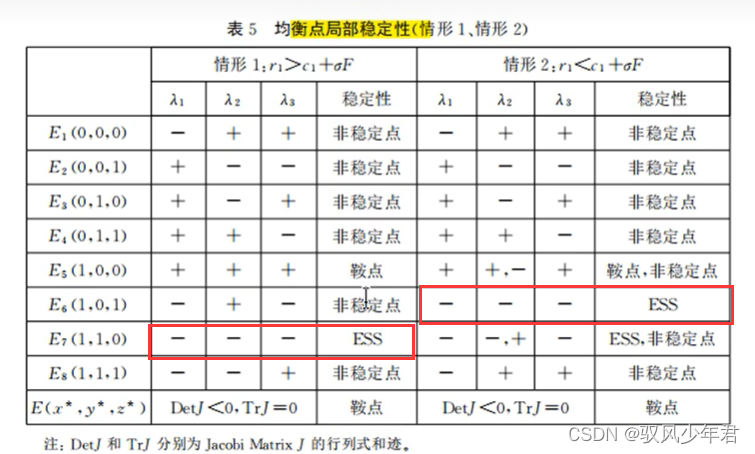
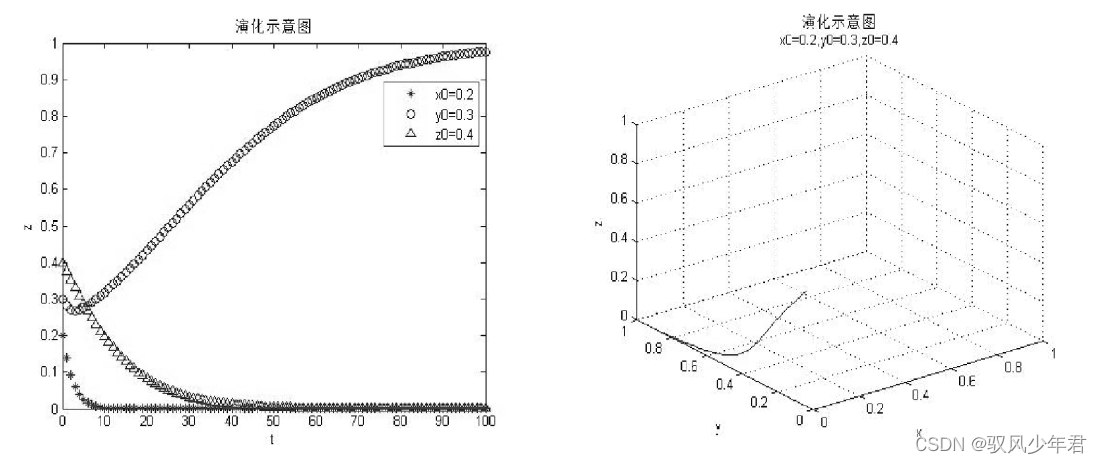
接下来,就可以进行模拟仿真的分析,可以借助Python,Matlab之内的工具进行实现
3.MatLAB的代码实现
%求均衡点及其特征值%
%(1)构建雅可比矩阵:diff是指求偏导
disp(['雅可比矩阵']):
A=[diff(fx,x) diff(fx,y) diff(fx,z);diff(fy,x) diff(fy,y) diff(fy,z);diff(fz,x) diff(fz,y) diff(fz,z)]%(2〉求均衡点:首先构建等式数组,然后使用solve函数来计算均衡点,输出对应的均衡点,最后构建均衡点数
equ=[fx==0,fy==0,fz==0];
answ=solve (equ,[x,y,z]);
%输出均衡点数组
disp(['均衡点:']):A1=[answ.x, answ.y, answ.z]
%均衡点个数
disp(['均衡点个数']):length(answ.x)
最后一点代码,不打了,有需要自己对应打把


这篇关于【学术小白成长之路】03三方演化博弈(基于复制动态方程)均衡点与稳定性分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






