本文主要是介绍信息学奥赛初赛天天练-21-完善程序-动态规划、编辑距离与字符数组应用的极致探索,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
PDF文档公众号回复关键字:20240606

1 2023 CSP-J 完善程序2
完善程序(单选题,每小题 3 分,共计 30 分)
给定两个字符串,每次操作可以选择删除(Delete)、插入(Insert)、替换(Replace),一个字符,求将第一个字符串转换为第二个字符串所需要的最少操作次数。
源程序
01 #include <iostream>
02 #include <string>
03 #include <vector>
04 using namespace std;
05
06 int min(int x,int y,int z){
07 return min(min(x,y),z);
08 }
09
10 int edit_dist_dp(string str1,string str2){
11 int m=str1.length();
12 int n=str2.length();
13 vector<vector<int>> dp(m+1,vector<int>(n+1));
14
15 for(int i=0;i<=m;i++){
16 for(int j=0;j<=n;j++){
17 if(i==0)
18 dp[i][j]=①;
19 else if(j==0)
20 dp[i][j]=②;
21 else if(③)
22 dp[i][j]=④;
23 else
24 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],⑤);
25 }
26 }
27 return dp[m][n];
28 }
29
30 int main(){
31 string str1,str2;
32 cin>>str1>>str2;
33 cout<<"Mininum number of operation:"
34 <<edit_dist_dp(str1,str2)<<endl;
35 return 0;
36 }
38 ①处应填( )
A j B i C m D n
39 ②处应填( )
A j B i C m D n
40 ③处应填( )
A str1[i-1]==str2[j-1] B str1[i]==str2[j]
C str1[i-1]!=str2[j-1] D str1[i]!=str2[j]
41 ④处应填( )
A dp[i-1][j-1]+1 B dp[i-1][j-1]
C dp[i-1][j] D dp[i][j-1]
42 ⑤处应填( )
A dp[i][j] + 1 B dp[i-1][j-1]+1
C dp[i-1][j-1] D dp[i][j]
2 相关知识点
1) 动态规划
动态规划(Dynamic Programming):简称 DP,是一种求解多阶段决策过程最优化问题的方法。在动态规划中,通过把原问题分解为相对简单的子问题,先求解子问题,再由子问题的解而得到原问题的解
动态规划最早由理查德 · 贝尔曼于 1957 年在其著作动态规划(Dynamic Programming)一书中提出。这里的 Programming 并不是编程的意思,而是指一种表格处理方法,即将每一步计算的结果存储在表格中,供随后的计算查询使用
2) 动态规划特征
最优子结构
指的是一个问题的最优解包含其子问题的最优解
即一个问题的最优解可以通过子问题的最优解计算而来,这样就可以使用子问题的解
重叠子问题
指的是在求解子问题的过程中,有大量的子问题是重复的,一个子问题在下一阶段的决策中可能会被多次用到
即大量重复的子问题,只需要对其求解一次,用表格将结果存储下来,求解原问题时大大提高计算效率
无后效性
指的是子问题的解(状态值)只与之前阶段有关,而与后面阶段无关。当前阶段的若干状态值一旦确定,就不再改变,不会再受到后续阶段决策的影响
即一旦某个子问题的解确定后,就不会再被改变
特征对比
最优子结构为求解原问题的解可以利用子问题的解的可能,无后效性,确保求解原问题最优解时子问题最优解一定可用
重叠子问题的存在,求解子问题时会出现多次重复求解子问题,动态规划的子问题存储,保证了重叠的子问题只计算1次存储,后续查询表格使用
3) dp数组
把原问题分解成若干子问题,每个子问题求解过程称为一个阶段,每一阶段求解结果记录到表格中,存储到dp数组中
dp数组中的元素存放每一阶段子问题的目标解
求解更复杂问题解时,如果用到子问题的解,直接到dp数组取出使用
3 思路分析
编辑距离
初始化dp数组
考虑str1不取任何字符,str2不取任何字符,因此dp数组的长度要是行数和列数是str1和str2长度加1
0行是空字符分别变成str1,前i个字符需要的最少操作次数
0列是空字符分别变成str2,前j个字符需要的最少操作次数
需要分别对0行0列进行初始化数据
后面dp数组的值根据0行0列的数据,和状态转移方程计算获得
状态转移
dp[i] [j] 表示str1中,前i个字符,变换到str2中前j个字符,需要操作的最少次数
//str1为abc ,str2为def时
//考虑求解dp[i][j]时,即考虑str1和str2最后一个字符,分2种情况,str1[i]和str2[j]是否相同
1 结尾相同
//str1[i]==str2[j] 时 ,str1为abcg,str2为defg时,等价于str1为abc,str2为def时需要操作的最少次数
dp[i][j]=dp[i-1][j-1]
2 结尾不同 插入
//str1[i]!=str2[j] 时,可能进行插入,删除,替换
//插入一个字符 str1为abc,str2为def,f插入到abc后,str1为abcf,str为def,此时结尾都是f,str1多了一个字符
//结尾相同 dp[i-1][j-1],str1多了一个字符,dp[i][j-1],做了一次插入操作+1
dp[i][j]=dp[i][j-1]+1
3 结尾不同 删除
//删除一个字符 str1为abc,str2为def,对def插入c后,str2为defc,此时结尾都是c,针对str1相等于删除了c
//结尾相同 dp[i-1][j-1],str2多了一个字符,dp[i-1][j],str2做了一次插入操作+1
dp[i][j]=dp[i-1][j]+1
4 结尾不同 更新
//更新结尾字符 str1为abc,str2为def,用f更新c,变成abf,def,都是f结尾
//结尾相同 dp[i-1][j-1] ,对abc中字符c更新成了f,做了1次更新操作+1
dp[i][j]=dp[i-1][j-1]
5 结尾不同时 取最小
//结尾不同时的3种情况,需要最少的操作次数,所以取3种情况的最小值
min(dp[i][j]=dp[i][j-1]+1,dp[i][j]=dp[i-1][j]+1,dp[i][j]=dp[i-1][j-1])
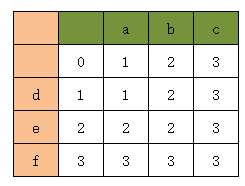
dp数组值
str1为abc,str2为def时,对应的dp数组
38 ①处应填( )
A j B i C m D n
答案 A
分析
i为0时,填dp数组第0行的值,第0行是空字符变成后面每1列需要对应列数次操作,列数为j
空列时0次,a列时1次,b列时2次,c列时3次
39 ②处应填( )
A j B i C m D n
答案 B
分析
j为0时,填dp数组第0列,第0列时空字符变成后面每行的操作次数,即i次
空行时为0,d行时为1,e行时为2,f行时为3
40 ③处应填( )
A str1[i-1]==str2[j-1] B str1[i]==str2[j]
C str1[i-1]!=str2[j-1] D str1[i]!=str2[j]
答案 A
分析
//str1和str2每加入1个字符时,求解最小操作次数
//此时需要判断最后1个字符是否相等
//正常情况下应该判断str1[i]==str2[j],由于dp数组的0行0列单独赋值,str1[0],str2[0]赋值为dp[1][1]
//并且循环是[0~m],[0~n]
//dp数组对应str1,str2下标是从1,1开始的,str1,str2是从0,0开始的
//所以填第i行时对应的是str1和str2是str1[i-1],str2[j-1]
15 for(int i=0;i<=m;i++){
16 for(int j=0;j<=n;j++){
17 if(i==0)
18 dp[i][j]=①;
19 else if(j==0)
20 dp[i][j]=②;
21 else if(③)
22 dp[i][j]=④;
23 else
24 dp[i][j]=1+min(dp[i][j-1],dp[i-1][j],⑤);
25 }
26 }
41 ④处应填( )
A dp[i-1][j-1]+1 B dp[i-1][j-1]
C dp[i-1][j] D dp[i][j-1]
答案 B
分析
结尾字符相同时
str1[i]==str2[j] 时 ,str1为abcg,str2为defg时,等价于str1为abc,str2为def时需要操作的最少次数
42 ⑤处应填( )
A dp[i][j] + 1 B dp[i-1][j-1]+1
C dp[i-1][j-1] D dp[i][j]
答案 C
分析
结尾不同的3种情况少了更新,所以选C
2 结尾不同 插入
//str1[i]!=str2[j] 时,可能进行插入,删除,替换
//插入一个字符 str1为abc,str2为def,f插入到abc后,str1为abcf,str为def,此时结尾都是f,str1多了一个字符
//结尾相同 dp[i-1][j-1],str1多了一个字符,dp[i][j-1],做了一次插入操作+1
dp[i][j]=dp[i][j-1]+1
3 结尾不同 删除
//删除一个字符 str1为abc,str2为def,对def插入c后,str2为defc,此时结尾都是c,针对str1相等于删除了c
//结尾相同 dp[i-1][j-1],str2多了一个字符,dp[i-1][j],str2做了一次插入操作+1
dp[i][j]=dp[i-1][j]+1
4 结尾不同 更新
//更新结尾字符 str1为abc,str2为def,用f更新c,变成abf,def,都是f结尾
//结尾相同 dp[i-1][j-1] ,对abc中字符c更新成了f,做了1次更新操作+1
这篇关于信息学奥赛初赛天天练-21-完善程序-动态规划、编辑距离与字符数组应用的极致探索的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







