opencv进阶 ——（十二）基于三角剖分实现人脸对齐

本文主要是介绍opencv进阶 ——（十二）基于三角剖分实现人脸对齐，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

 三角剖分概念  

        三角剖分（Triangulation）是一种将多边形或曲面分解为一系列互不相交的三角形的技术，它是计算几何、计算机图形学、地理信息系统、工程和科学计算中的一个基本概念。通过三角剖分，复杂的形状可以被简化为基本的三角形元素，这些元素更容易处理和分析。

在二维空间中，一个简单的三角剖分将一个多边形划分为若干个不相交的三角形，这些三角形的边要么是多边形的边，要么是连接多边形内部点的边。在三维空间中，三角剖分通常应用于表面建模，将一个曲面分割成一系列互不相交的三角面片。

三角剖分有多种类型，其中最著名的一种是Delaunay三角剖分。在Delaunay剖分中，一个点的邻接三角形的内切圆（包含该点但不包含其他点的最小圆）是唯一的，且该点位于圆的外部。这种剖分在很多应用中非常有用，因为它保证了相邻三角形之间的良好分布，从而避免了过于狭长的三角形，这对于数值计算和图形渲染来说是理想的。

三角剖分在以下领域有广泛应用：

• 计算机图形学：在3D建模和渲染中，用于将复杂的模型简化为三角面片，便于计算和显示。
• 地理信息系统（GIS）：用于将地图数据分割成三角形网格，便于空间分析和数据可视化。
• 有限元分析（FEM）：在工程计算中，用于将连续区域划分为离散的三角形单元，以便于数值求解偏微分方程。
• 游戏开发：在游戏引擎中，用于减少模型的多边形数量，提高渲染效率。
• 机器学习：在某些算法中，比如最近邻搜索，Delaunay三角剖分可以作为数据结构加速计算。

        三角剖分通常可以通过算法来实现，例如Graham扫描、 Jarvis March 或者更高效的算法如incremental方法和flip-based方法。在实际应用中，有许多现成的库和工具提供了三角剖分的功能，例如CGAL（Computational Geometry Algorithms Library）和Triangle库。 

人脸对齐实现   

实现步骤 

1、检测人脸区域

2、对人脸区域进行关键点标识

3、考虑到人脸可以存在倾斜，为了能更好的对齐效果，可以对关键点做旋转矩阵拟合

4、这里以经典的人脸68关键点为示例，为了边界部分更自然，可以对旋转矩阵进行扩展

5、将每一个三角形与目标三角形进行仿射变换得到一张与目标点对齐的人脸

代码实现

扩展旋转矩阵区域

void increaseRect(std::vector<cv::Point2f>& points,const cv::Mat& img)
{// 计算点集合构成的矩形的边界框cv::Rect rect = cv::boundingRect(points);// 定义增加比例float scale = 0.2;// 计算增加的宽度和高度int width = rect.width*scale;int height = rect.height*scale;// 定义增加值的lambda函数，用于安全地增加或减少一个值auto addVal = [](float& val, float add, float max){val = std::min(val + add, max); // 确保值不会超过最大值};auto subVal = [](float& val, float sub, float min){val = std::max(val - sub, min); // 确保值不会低于最小值};// 应用增加的宽度和高度来调整四个顶点的位置// 调整第一个点的x坐标和y坐标subVal(points[0].x, width, 0);addVal(points[0].y, height, img.rows);// 调整第二个点的x坐标和y坐标subVal(points[1].x, width, 0);subVal(points[1].y, height, 0);// 调整第三个点的x坐标和y坐标addVal(points[2].x, width, img.cols);subVal(points[2].y, height, 0);// 调整第四个点的x坐标和y坐标addVal(points[3].x, width, img.cols);addVal(points[3].y, height, img.rows);
}

增加边界点

void FillPointRect(const std::vector<cv::Point2f>& points,  std::vector<cv::Point>& vecPoint)
{// 临时存储扩充的点std::vector<cv::Point> addPointsTmp; // 根据原始点集，通过向每个点添加偏移量来生成新的点addPointsTmp.push_back(points[0] + cv::Point2f(1, -1));addPointsTmp.push_back(points[1] + cv::Point2f(1, +1));addPointsTmp.push_back(points[2] + cv::Point2f(-1, +1));addPointsTmp.push_back(points[3] + cv::Point2f(-1, -1));// 通过现有点计算并加入新的点，以构成矩形的外接多边形addPointsTmp.push_back((addPointsTmp[0]  + addPointsTmp[1])/2);addPointsTmp.push_back((addPointsTmp[1]  + addPointsTmp[2])/2);addPointsTmp.push_back((addPointsTmp[2]  + addPointsTmp[3])/2);addPointsTmp.push_back((addPointsTmp[3]  + addPointsTmp[0])/2);// 将扩充的点集添加到输出向量中vecPoint.insert(vecPoint.end(), addPointsTmp.begin(), addPointsTmp.end());
}

获取所有的三角形下标

//获取三角形下标
std::vector<cv::Vec3i> Triangulation::getTrianglesIndexs(std::vector<cv::Vec6f>& triangleList, std::vector<cv::Point>& vecPoint)
{auto findPoint = [&vecPoint](cv::Point& p){for (int i = 0; i < vecPoint.size(); i++){if (vecPoint[i] == p){return i;}    }return -1;};std::vector<cv::Vec3i> trianglesIndexs;for (auto& item : triangleList){cv::Point p1 = cv::Point(item[0], item[1]);cv::Point p2 = cv::Point(item[2], item[3]);cv::Point p3 = cv::Point(item[4], item[5]);auto idx1 = findPoint(p1);auto idx2 = findPoint(p2);auto idx3 = findPoint(p3);if (idx1 != -1 && idx2 != -1 && idx3 != -1){trianglesIndexs.push_back(cv::Vec3i(idx1, idx2, idx3));}}return trianglesIndexs;
}

绘制三角剖分图

std::vector<cv::Point> vecPoint = item.boxPoint;auto rotateRect = cv::minAreaRect(vecPoint);cv::Point2f pot[4];rotateRect.points(pot);std::vector<cv::Point2f> rotatePoints{pot[0], pot[1], pot[2], pot[3]};increaseRect(rotatePoints, img);FillPointRect(rotatePoints, vecPoint);std::vector<cv::Point> vecHull;cv::convexHull(vecPoint, vecHull);auto rect = cv::boundingRect(vecHull);cv::Subdiv2D subdiv(rect);std::vector<cv::Point2f> vecPoint2f;for (auto& ptIt : vecPoint){vecPoint2f.emplace_back(cv::Point2f(ptIt.x, ptIt.y));}subdiv.insert(vecPoint2f);std::vector<cv::Vec6f> triangleList;subdiv.getTriangleList(triangleList);auto trianglesIndexs = std::move(getTrianglesIndexs(triangleList, vecPoint));for (auto& item : trianglesIndexs){cv::Point pt1 = vecPoint[item[0]];cv::Point pt2 = vecPoint[item[1]];cv::Point pt3 = vecPoint[item[2]];cv::line(destDataOut->img(), pt1, pt2, 255);cv::line(destDataOut->img(), pt2, pt3, 255);cv::line(destDataOut->img(), pt3, pt1, 255);}

人脸对齐

cv::Mat alignmentImageData(const cv::Mat& srcImg, const cv::Rect& srcBox, std::vector<cv::Point> vecPointRoi, std::vector<cv::Point> vecDestPointRoi)
{auto srcImgRoi = srcImg(srcBox);//构建三角剖分，获取三角形下标cv::Subdiv2D subdiv(cv::Rect(0, 0, srcBox.width, srcBox.height));std::vector<cv::Point2f> vecPoint2f;vecPoint2f.insert(vecPoint2f.end(), vecPointRoi.begin(), vecPointRoi.end());subdiv.insert(vecPoint2f);std::vector<cv::Vec6f> triangleList;subdiv.getTriangleList(triangleList);auto trianglesIndexs = std::move(getTrianglesIndexs(triangleList, vecPointRoi));qDebug() << "triangles size:" << trianglesIndexs.size();cv::Mat destNewImg = srcImgRoi.clone();auto maxRoiSize = srcImgRoi.size();for (auto& item : trianglesIndexs){cv::Point tr1Pt1 = vecPointRoi[item[0]];cv::Point tr1Pt2 = vecPointRoi[item[1]];cv::Point tr1Pt3 = vecPointRoi[item[2]];auto rect1 = cv::boundingRect(std::vector<cv::Point>{tr1Pt1, tr1Pt2, tr1Pt3});auto croppedTriangle = srcImgRoi(rect1);cv::Point rect1Beg = cv::Point(rect1.x, rect1.y);cv::Point tr2Pt1 = vecDestPointRoi[item[0]];cv::Point tr2Pt2 = vecDestPointRoi[item[1]];cv::Point tr2Pt3 = vecDestPointRoi[item[2]];auto rect2 = cv::boundingRect(std::vector<cv::Point>{tr2Pt1, tr2Pt2, tr2Pt3});cv::Mat croppedTr2Mask = cv::Mat::zeros(rect2.size(),  CV_8UC1);//生成模板图像三角形掩码cv::Point rect2Beg = cv::Point(rect2.x, rect2.y);std::vector<cv::Point> maskPoints2 = {tr2Pt1 - rect2Beg, tr2Pt2 - rect2Beg, tr2Pt3 - rect2Beg};cv::fillConvexPoly(croppedTr2Mask, maskPoints2, 255);cv::Point2f srcTri[3] = {tr1Pt1 - rect1Beg, tr1Pt2 - rect1Beg, tr1Pt3 - rect1Beg};cv::Point2f dstTri[3] = {tr2Pt1 - rect2Beg, tr2Pt2 - rect2Beg, tr2Pt3 - rect2Beg};auto warpMat = cv::getAffineTransform(srcTri, dstTri);cv::Mat warpTriangle;cv::warpAffine(croppedTriangle, warpTriangle, warpMat, rect2.size());cv::bitwise_and(warpTriangle, warpTriangle, warpTriangle, croppedTr2Mask);cv::Mat roi = destNewImg(rect2);warpTriangle.copyTo(roi, croppedTr2Mask);}return  destNewImg;
}

人脸68关键点和5关键点三角剖分图

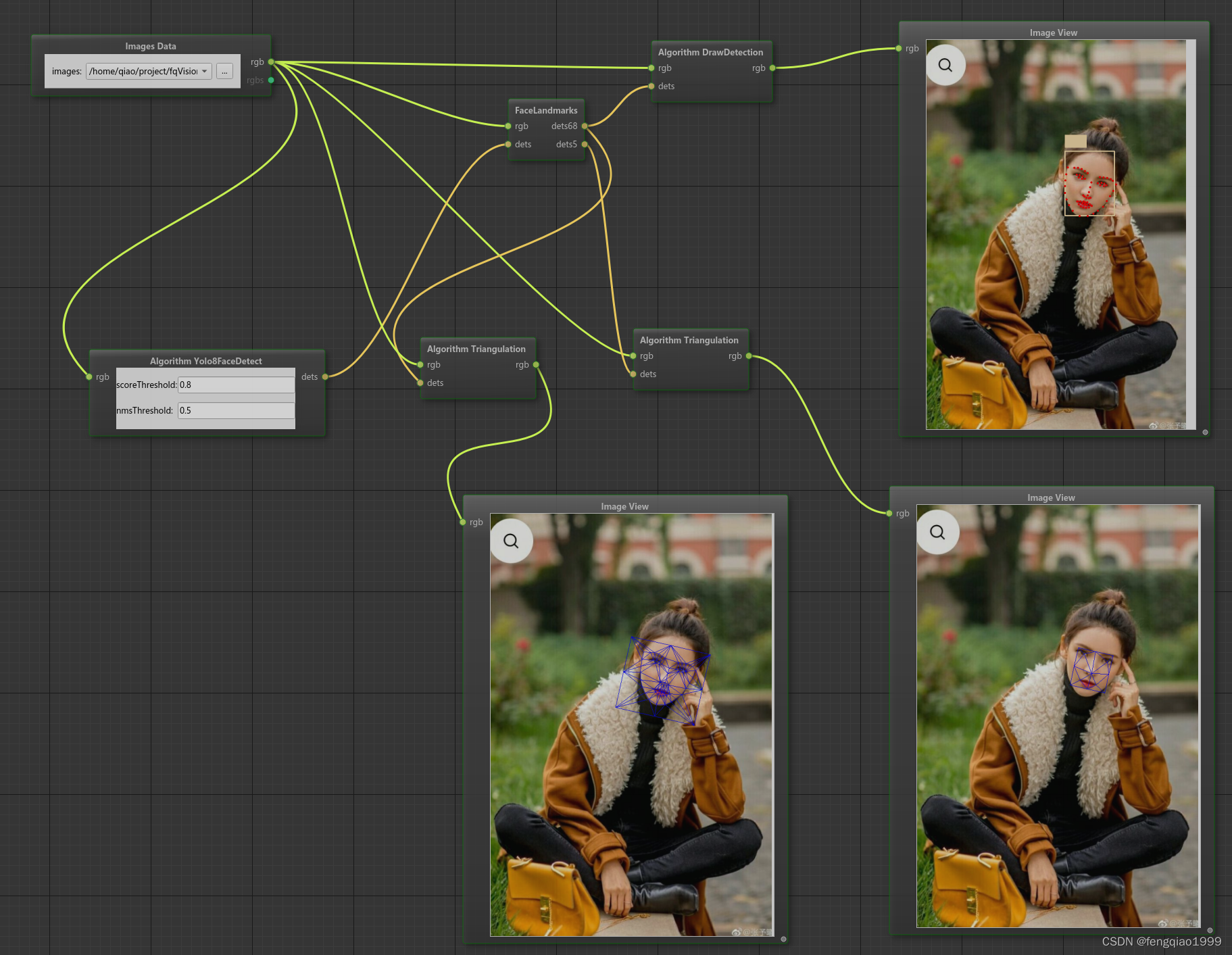
人脸对齐

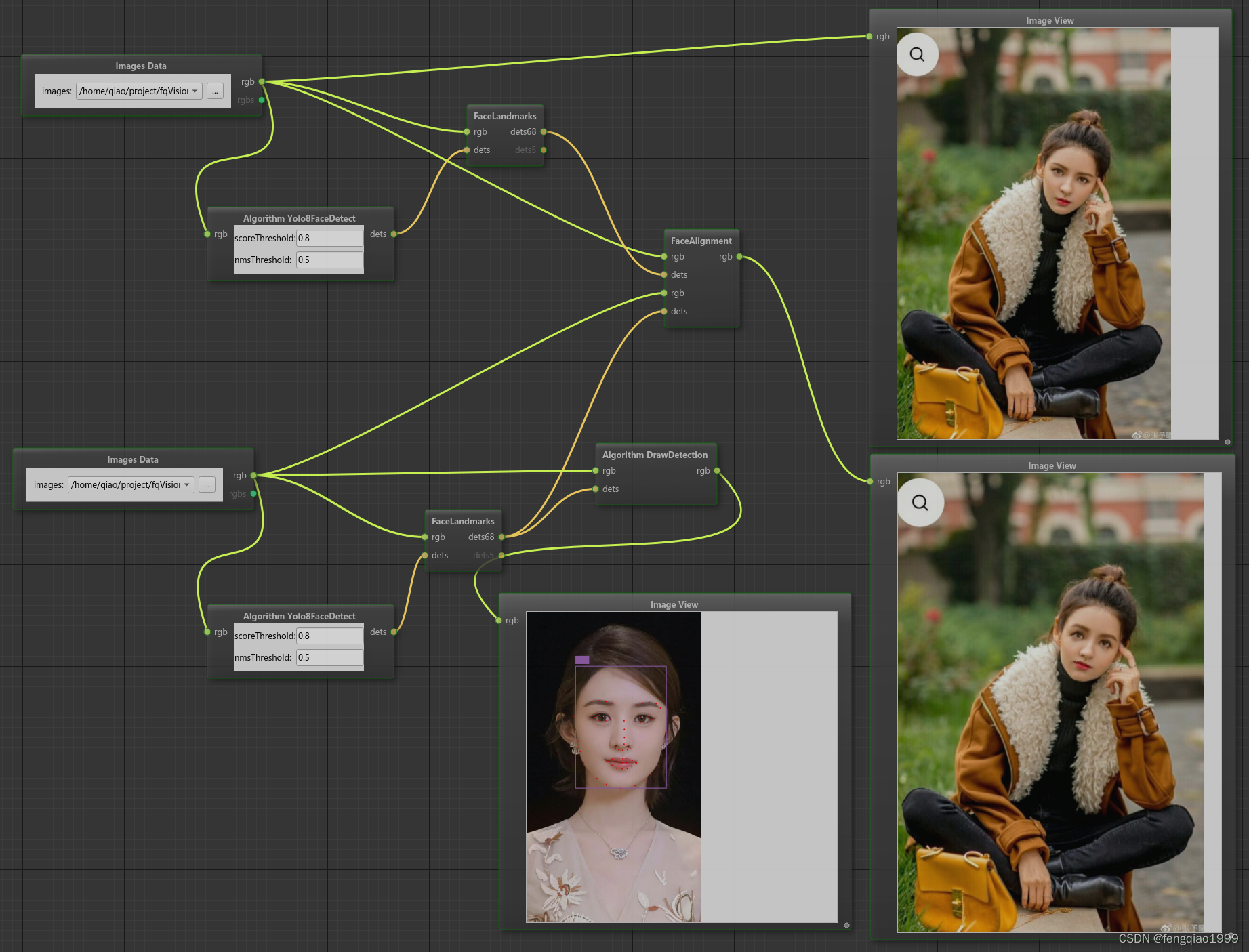
这篇关于opencv进阶 ——（十二）基于三角剖分实现人脸对齐的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---