本文主要是介绍太极图形课——渲染——光线追踪实战第一部分呢,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
根据概念部分我们逐步通过太极实现光线追踪
总共可以分为5步
第一步:如何发射出一道光?
首先明确何为一道光,光从我们眼睛(摄像机)射出,那么在三维虚拟世界里,我们可以认为这道光就是一条射线,在三维世界里,一条射线可以由一个点和一个向量定义

任何在这条射线上的点,我们都可以用一个标量t来表示,这个标量的值代表了这个点到射出去的原点的距离
那么我们如何把这样一条射线放进我们所定义的虚拟世界中呢,首先需要设定的就是在这个虚拟世界中我们眼睛(摄像机)的位置,这个位置通过三维世界的坐标一个三维的数组就可以表达了,第二就是定义我们看的方向,也就是方向向量,也通过一个三维的数组表达
在概念中说,最后我们要将三维的物体投影在眼前的屏幕上就可以了,那么我们就需要放置屏幕,我们所看的方向穿过这个屏幕的中心,这个屏幕垂直于我们的视线

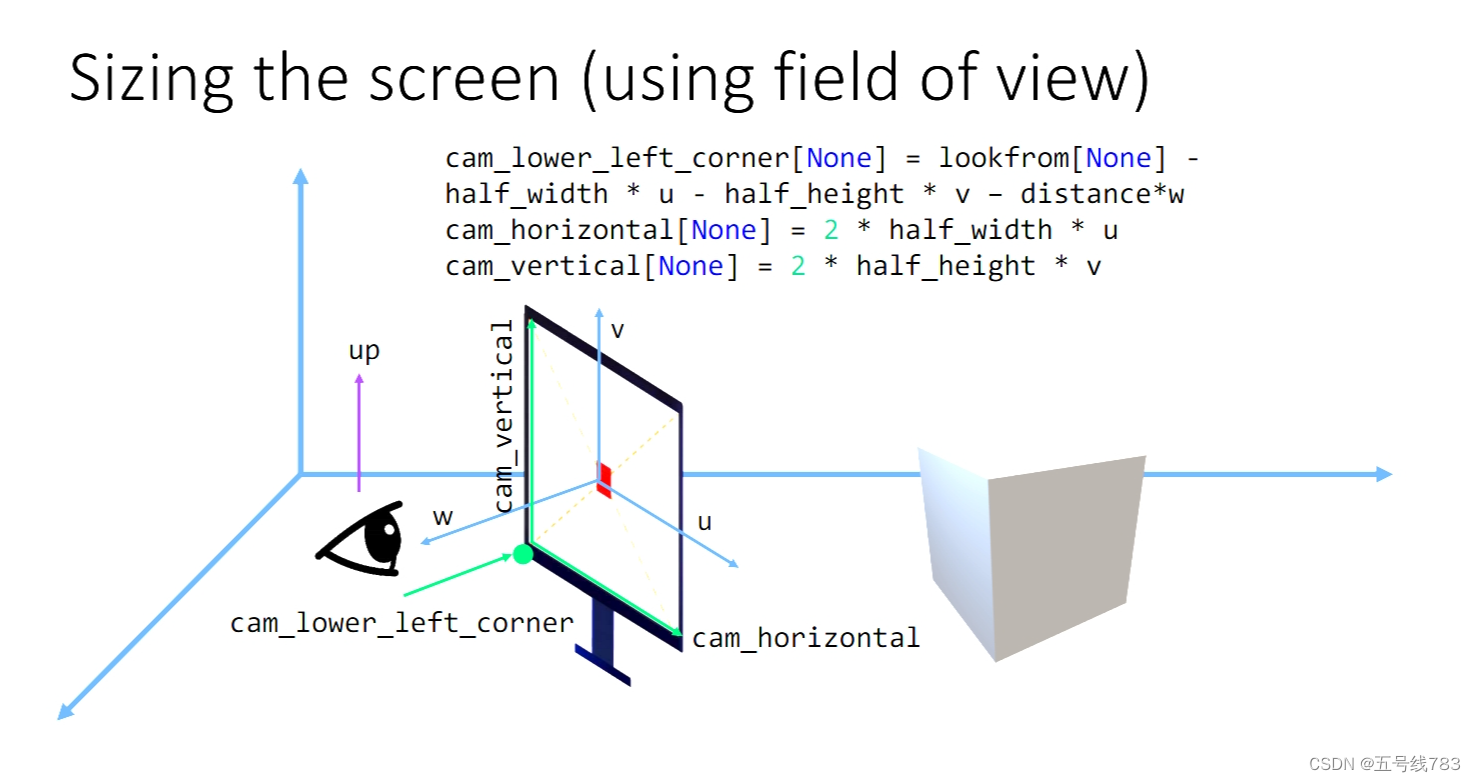
现在屏幕的位置还没有确定,首先我们需要确定屏幕和我们眼睛的距离,再确定屏幕屏幕的方向,我们设定一个三维向量来确定,最后就是屏幕的大小,这个我们通过设定一个fov来表示

通过fov可以求出屏幕的半宽和半长,宽由长决定,取决于你需要几比几的屏幕,例如16:9,有了这些我们设定一个以屏幕中心为原点的坐标系uvw,最后可以确定眼睛或者说摄像机左下角出发的点,并确定其水平和垂直的向量
此时我们就已经准备好发射射线
#首先定义一个世界坐标系,其中有眼睛或者说摄像机的位置
lookfrom[None] = [x,y,z]
#定义朝向
lookat[None] = [x,y,z]
#定义屏幕和其中心点
theta = 1.0/3.0 *pi #fov设置
half_height = ti.tan(theta/2.0) *distance
half_width = aspect_ratio * half_height * distance
w = (lookfrom[None] - lookat[None]).normalized()
u = (upp[None].cross(w)).normalized()
v = w.cross(u)
#可以得到屏幕的视点位置
cam_lower_left_corner[None] = (lookfrom[None] - half_width*u - half_height *v - w)*distance
cam_horizational[None] = 2* half_width * u * distance
cam_vertical[None] = 2 * half_height * v *distance
#发射光线
u = float(j)/res_x
v = float(i)/res_Y
ray.direction = cam_lower_left_corner[None] + u * cam_horizational[None] + v * cam_vertical[None] - lookfrom[None]
#pixel块是一个像素点方块,我们可以将其放在正中间
u = float(i + 0.5)/res_x
v = float(j + 0.5)/res_y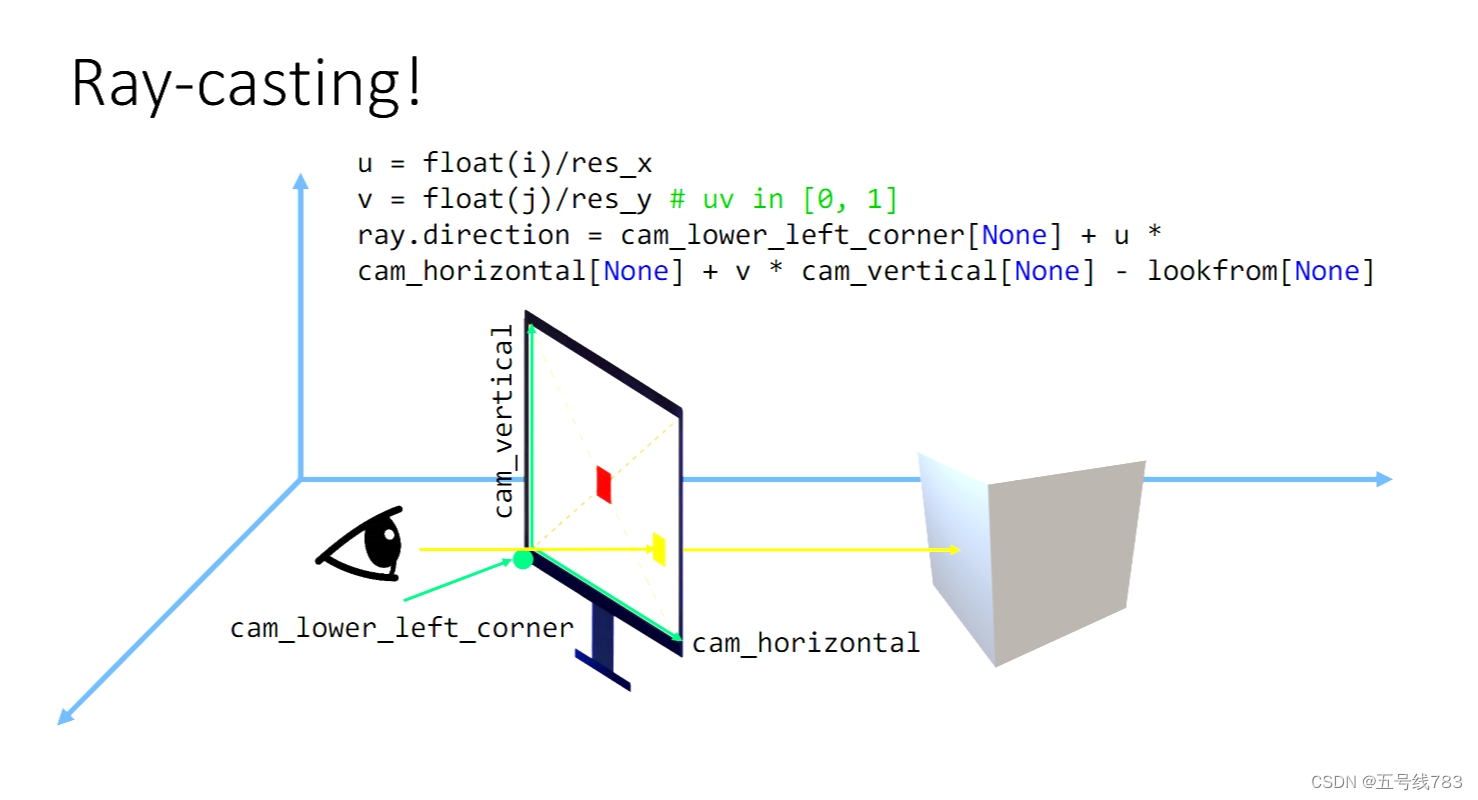
由于像素是一个方块,我们还可以把这个射线正好移动到点的中心

第二步: 如何将光和物体求交
之前已经了解到一个视线由一个射线表示,射线上的每一个点可以通过一个标量t来表示,那么怎么实现物体和实现的求交呢,对于一个圆来说。我们可以将圆用一个参数方程来表示,然后将点用t来代替我们就可以得到下列的方程


将方程简化就可以获得一个一元二次方程


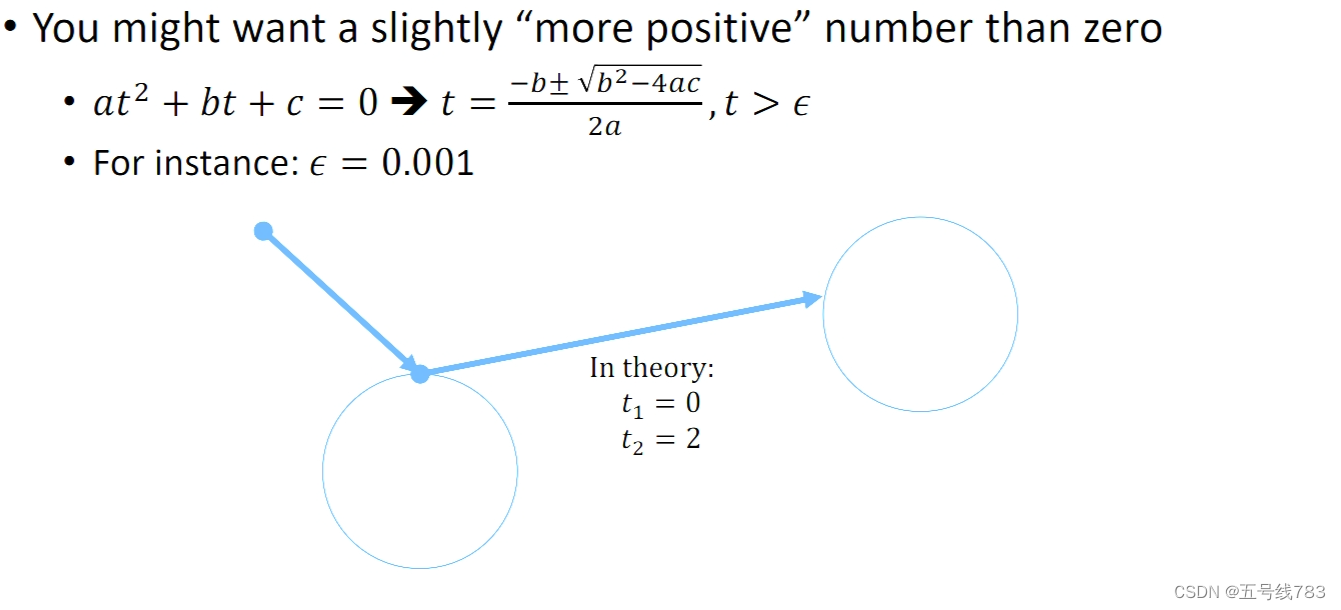
通过求根公式韦达定理,可以判断是否有相交,相交的点是哪一个,我们需要去第一个正根,在计算机中由于有时候会出现0.0001这种明显是物体没有相交而是反射的正根,因此需要添加一个门槛,例如正根至少要大于0.001
目前教程所给代码中仅仅只实现了与圆的相交,实际上还可以实现和平面,三角形实现相交,例如对于一个平面来说,我们
的参数方程可以定义为平面上任意两个点所构成的向量和平面的法向量垂直,也就是点乘为0,将任意一点用视线的点代替

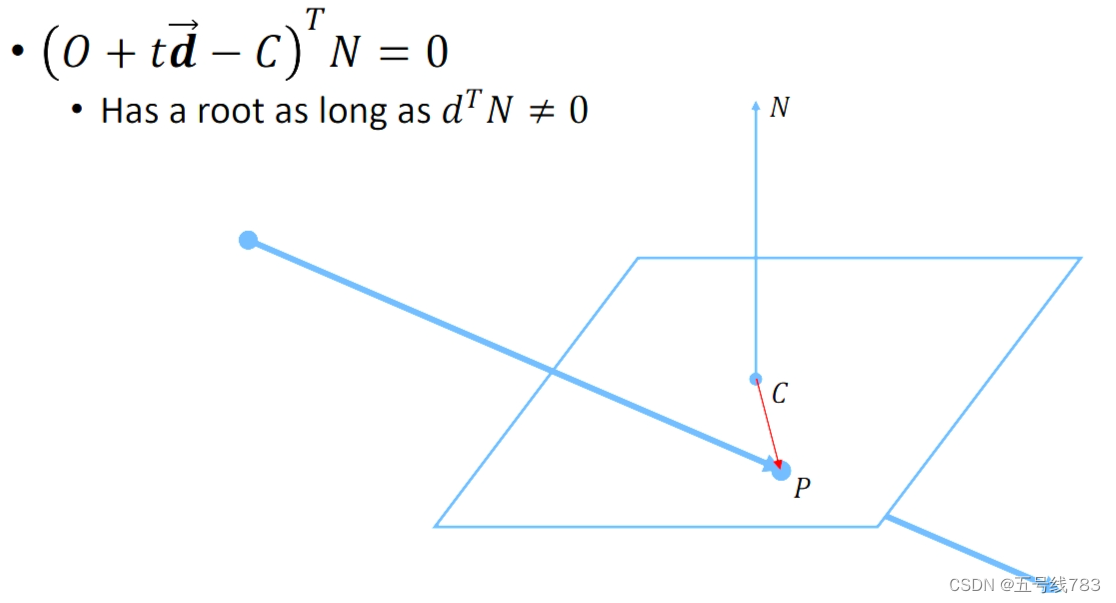
可以获得的根的方程为向量d和法向量点乘不为0,也就是这两个方向不垂直的时候,一定有一个点
 、
、
如果为点乘为0,也分为从平面出发导致与平面重合以及不从平面出发,永远没有交点
进一步如何判断有点的话是否该点在三角形内

此时需要引入的概念是重心的概念,具体概念如下图,三个三角形的面积相加等于整个三角形说明这个点在三角形内
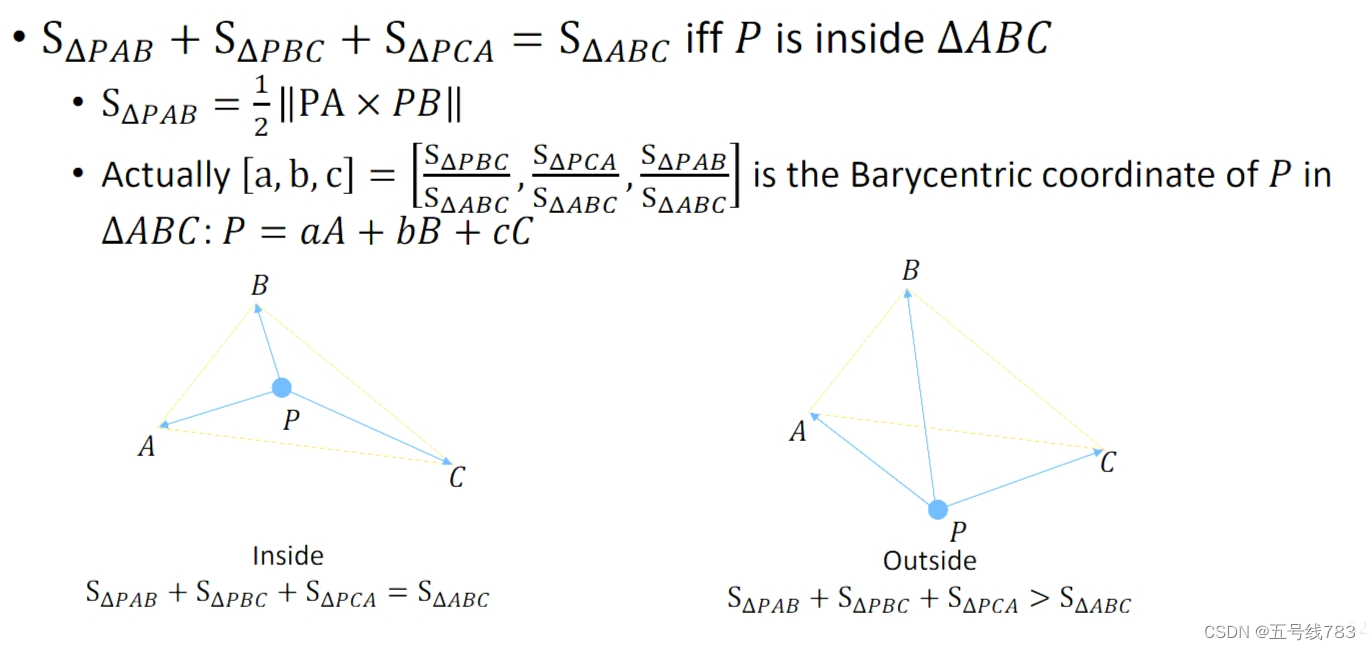
这个重心的概念可以推广到四面体上
此时就可以判断三角形网格的相交了

最后可以得到两种方法,一种是隐式积分,找到面的定义,将点的定义代入其中,最后得到一个高纬的方程,简化后都是一个一元二次方程,第二种方法遍历全部的三角形面片,找到点在哪个三角形里面
这篇关于太极图形课——渲染——光线追踪实战第一部分呢的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




