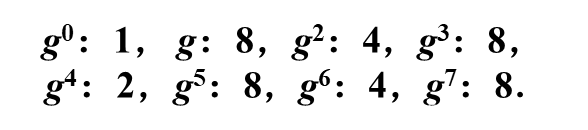网络空间安全数学基础·循环群、群的结构

本文主要是介绍网络空间安全数学基础·循环群、群的结构，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

3.1 循环群（重要）
3.2 剩余类群（掌握）
3.3 子群的陪集（掌握）
3.4 正规子群、商群（重要）

3.1 循环群

定义：如果一个群G里的元素都是某一个元素g的幂，则G称为循环群。g称为G的一个生成元，由g生成的循环群记为(g)或<g>。
无限循环群可表示为：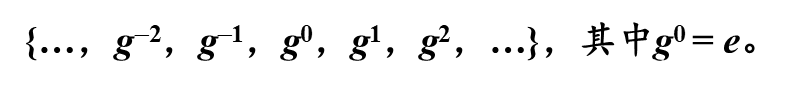

有限n阶循环群可表示为：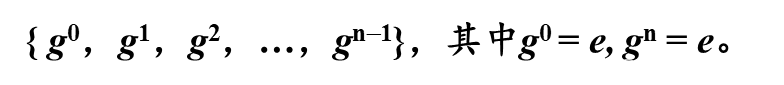

例：整数加法群Z是一个循环群。1是生成元，每一个元素都是1的“幂”。再次强调讨论的群里“乘法”是抽象的，只代表一种代数运算．在整数加群中，“乘法”就是普通加法，那么“幂”就是一个元素的连加，例如
，。

而且规定

即0为0个1相加。

循环群简单性质：
n阶循环群中g^n = e，得：设i，j是任意整数，如果i≡j (mod n)，则g^i = g^j，g^i的逆元g^i = g^(n-i)是交换群。
对于循环群G中两个任意元，循环群一定满足交换律，是交换群(Abel群)。在n阶循环群中，有g^n = e。

设G是一个群，a是G中的一个元素。
1) a的所有幂两两不相等，于是以a为生成元的循环群是无限循环群。
2) 存在整数i>j，使a^i = a^j，则a^(i-j)=e。这表明存在正整数k = i-j 使a^k = e。使上式成立的最小正整数k称为元素a的阶。在第1种情况下，这样的正整数不存在，称a是无限阶元素。

元素的阶及其性质：
a是n阶元素，则序列两两不相同，而且a的一切幂都包含在这个序列中。
定理：一个群G的任意元素a都能生成一个循环群，它是G的子群。如果a是无限阶元素，则a生成无限循环群，如果a是n阶元素，则a生成n阶循环群。
定理：对于n阶元素a有a^i = e，当且仅当n|i。a^k 的阶为 n/(k,n)。
推论：元素g生成的n阶循环群G中元素g^k(0＜k≤n-1)的阶为 n/(k,n)；当k，n互素时，g^k的阶为n，也是G的生成元。

例：8阶循环群各个元素的阶分别为：

其中共有4个生成元

整数集合{0,1,2…,n-1}中与n互素的数有φ(n)个(欧拉函数)，因此n阶循环群共有φ(n)个n阶元素即φ(n)个生成元。

定理：
1) 循环群的子群是循环群，它或者仅由单位元构成，或者由子群中具有最小正指数的元素生成，即生成元为具有最小正指数的元素；
2) 无限循环群的子群除{e}外都是无限循环群；
3) n阶循环群的子群的阶是n的正因子，且对n的每一个正因子q，有且仅有一个q阶子群。

例：8阶循环群G的真子群。
8的所有正因子为1，2，4，8, 相应的子群分别为: (因为8=1·8=2·4=4·2=8·1）

其中{e}和G是群G的平凡子群。

3.2 剩余类群

剩余类：根据同余的概念，可以将整数Z进行分类：设m是正整数，把模m同余的整数归为一类，即可表示为 a = qm+r， 0≤r＜m，q = 0，±1，±2，… 。这一类，称为剩余类，剩余类中的每个数称为该类的剩余或代表，r称为该类的最小非负剩余。

剩余类群：
将全体整数按模m分成m个剩余类：
或
= {0，±m，±2m，±3m，…}；

= {1，1±m，1±2m，1±3m，…}；
= {2，2±m，2±2m，2±3m，…}；
…
= {(m-1)，(m-1)±m，(m-1)±2m ，…}
这m个剩余类称为模m剩余类，记为Zm。

设和是两个模m的剩余类，定义剩余类的加法如下：。

例：如Z8的两个剩余类和，。

定理：模m的全体剩余类集合对于剩余类加法构成m阶循环群。称为m阶剩余类加群。
定理：任意无限循环群与整数加群Z同构；任意n阶循环群与n阶剩余类加群同构。

3.3 子群的陪集

引理：
设G是一个群。
1) 对于任意a∈G，集合 aG = {ah | h∈G}= G。
2) GG = {ah | h∈G，a∈G}= G。

定义：设H是群G的一个子群。对于任意a∈G，集合 aH={ah | h∈H } 称为H的一个左陪集。同样定义右陪集 Ha = {ha | h∈H }。对于交换群，左陪集和右陪集是一致的，可以称为陪集。

陪集的性质：
(1)
(2)这说明陪集中的任何元素均可以作为代表元。
(3)两个陪集相等的条件
(4)对任何a, b∈G有aH = bH 或。因而H的所有左陪集的集合{aH︱a ∈G}构成了G的划分。

定理：设H是群G的一个子群。H的任意两个左（右）陪集或者相等或者无公共元素。群G可以表示成若干互不相交的左（右）陪集的并集。

例：设m是一个正整数，M表示所有m的倍数组成的集合，即M = {mt | t = 0，±1，±2，±3，… } = {0，±m，±2m，±3m，…}， M的另一种表示为M = {mt | t∈Z}。

显然M是整数加群Z的子群。

设为模m的一个剩余类，即于是有。

可见是M的一个陪集。由Z可以按模m分成m个剩余类，则Z可以按M分成m个陪集： M，1+M，2+M，…，(m-1)+M。