[Algorithm][动态规划][子序列问题][最长定差子序列][最长的斐波那契子序列的长度]详细讲解

本文主要是介绍[Algorithm][动态规划][子序列问题][最长定差子序列][最长的斐波那契子序列的长度]详细讲解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

1.最长定差子序列

1.题目链接

• 最长定差子序列

---

2.算法原理详解

• 思路：

  • 确定状态表示 -> dp[i]的含义

    • 以i位置元素为结尾的所有子序列中，最长的等差子序列的长度

  • 推导状态转移方程
    

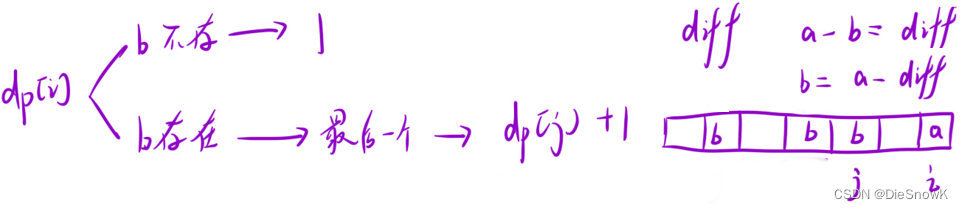
  • 优化：

    • 将元素 + dp[j]的值，绑定存放进哈希表中
      • 这样就不用每次都从前向后遍历原数组找值了
    • 直接在哈希表中，做动态规划

  • 初始化：hash[arr[0]] = 1

  • 确定填表顺序：从左往右

  • 确定返回值：整个dp表里的最大值

---

3.代码实现

int longestSubsequence(vector<int>& arr, int difference) 
{unordered_map<int, int> hash; // <arr[i], dp[i]>hash[arr[0]] = 1;int ret = 0;for(int i = 1; i < arr.size(); i++){// 1.如果arr[j]不存在，那么arr[i]就会被初始化为1// 2.如果出现重复的值，那么后面出现的值会覆盖掉前面的值hash[arr[i]] = hash[arr[i] - difference] + 1; ret = max(ret, hash[arr[i]]);}return ret;
}

---

2.最长的斐波那契子序列的长度

1.题目链接

• 最长的斐波那契子序列的长度

---

2.算法原理详解

• 思路：

  • 确定状态表示 -> dp[i]的含义

    • dp[i]：以i位置元素为结尾的所有的子序列中，最长的斐波那契子序列的长度 -> 无法正确表示状态
      • 因为虽然可以找到i前一个值，但是却无法得知此时它前一个数是什么，现在的规模到哪一步了
    • dp[i][j]：以i位置以及j位置的元素为结尾的所有的子序列中，最长的斐波那契子序列的长度(i < j)

  • 推导状态转移方程
    

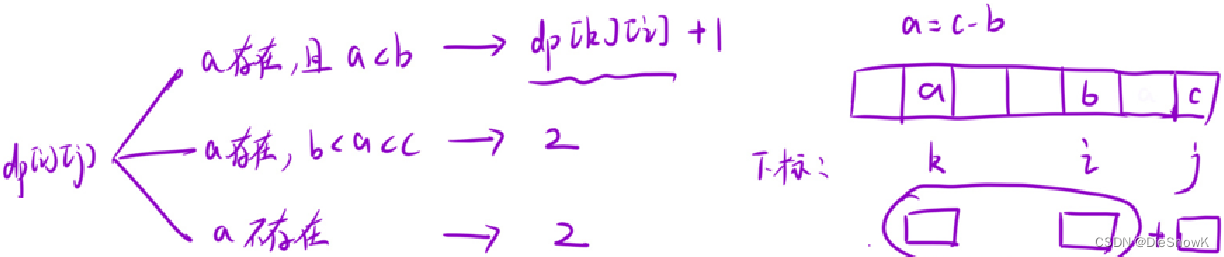
  • 优化：将数组中所有元素与它们的下标绑定，存在哈希表中，这样有利于提升查找效率

  • 初始化：vector<vector<int>> dp(n, vector<int>(n, 2))

  • 确定填表顺序：从上往下

  • 确定返回值：dp表里的最大值：ret < 3 ? 0 : ret

---

3.代码实现

int lenLongestFibSubseq(vector<int>& arr) 
{int n = arr.size();// 优化unordered_map<int, int> hash; // <arr[i], i>for(int i = 0; i < n; i++){hash[arr[i]] = i;}vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for(int j = 2; j < n; j++) // 固定第一个位置{for(int i = 1; i < j; i++) // 固定第二个位置{int a = arr[j] - arr[i];if(a < arr[i] && hash.count(a)){dp[i][j] = dp[hash[a]][i] + 1;ret = max(ret, dp[i][j]);}}}return ret < 3 ? 0 : ret;
}

这篇关于[Algorithm][动态规划][子序列问题][最长定差子序列][最长的斐波那契子序列的长度]详细讲解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---