从零开始学习Slam-旋转矩阵旋转向量四元组（二）

本文主要是介绍从零开始学习Slam-旋转矩阵旋转向量四元组（二），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文参考：计算机视觉life 仅作笔记用
书接上回，上回不清不楚的介绍了旋转矩阵&旋转向量和四元组
现在回顾一下重点：
本着绕谁谁不变的变则
假设绕z轴旋转θ，旋转矩阵为：
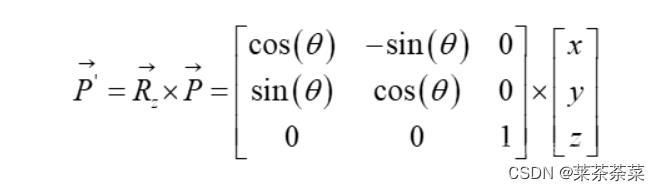
在这里插入图片描述
再回顾一下旋转向量的表示以及这个基本记不住的罗德里格斯公式，记不住也没事：

一个例子

已知旋转矩阵定义是沿着Z轴旋转45°。请按照该定义初始化旋转向量、旋转矩阵、四元数、欧拉角。请编程实现：

1、以上四种表达方式的相互转换关系并输出，并参考给出的结果验证是否正确。

2、假设平移向量为（1,2,3）,请输出旋转矩阵和该平移矩阵构成的欧式变换矩阵，并根据欧式变换矩阵提取旋转向量及平移向量。

#include <iostream>
#include <Eigen/Dense>using namespace Eigen;int main() {// 初始化旋转参数double angle = M_PI/4; // 45°转换为弧度Vector3d axis = Vector3d::UnitZ(); // Z轴// 初始化旋转向量Vector3d rotation_vector = angle * axis;// 初始化旋转矩阵Matrix3d rotation_matrix;// AngleAxisd(angle, axis) 创建了一个表示绕着给定轴 axis 旋转 angle 弧度的旋转向量。//在Eigen库中，AngleAxisd 类表示一个旋转向量，它由一个旋转轴和一个旋转角度组成。//它的构造函数可以接受旋转角度和旋转轴作为参数，也可以接受一个旋转矩阵作为参数，并从中提取旋转轴和旋转角度。//调用 toRotationMatrix() 方法将该旋转向量转换为对应的旋转矩阵。rotation_matrix = AngleAxisd(angle, axis).toRotationMatrix();// 初始化四元数Quaterniond quaternion(rotation_matrix);// 初始化欧拉角Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // ZYX顺序// 输出四种表达方式 // 旋转向量std::cout << "Rotation Vector: " << rotation_vector.transpose() << std::endl;  // .transpose()方法被用于将向量和矩阵输出成为行向量的形式，以方便显示在控制台上。// 旋转矩阵std::cout << "Rotation Matrix:\n" << rotation_matrix << std::endl;// coeffs()方法用于获取四元数对象的系数，返回一个四维向量。std::cout << "Quaternion: " << quaternion.coeffs()<< std::endl;// 欧拉角std::cout << "Euler Angles (ZYX): " << euler_angles.transpose() << std::endl;// 假设平移向量为（1,2,3）Vector3d translation_vector(1, 2, 3);// 构造欧式变换矩阵Matrix4d euclidean_transform_matrix = Matrix4d::Identity();  // 创建一个4x4的单位矩阵的静态方法// 将旋转矩阵赋值给欧几里德变换矩阵的左上角的3x3子矩阵，即旋转部分euclidean_transform_matrix.block<3,3>(0,0) = rotation_matrix;// 将平移向量赋值给欧几里德变换矩阵的右上角的3x1子矩阵，即平移部分euclidean_transform_matrix.block<3,1>(0,3) = translation_vector;/* 在Eigen库中，AngleAxisd()是用于创建一个旋转向量（Angle-Axis）的构造函数。Angle-Axis旋转表示通过一个旋转轴和一个旋转角度来描述旋转。具体来说，AngleAxisd()的使用方法如下Eigen::AngleAxisd angle_axis(angle, axis);在这段代码中，AngleAxisd(rotation_matrix)创建了一个AngleAxisd类型的对象，该对象代表了由旋转矩阵rotation_matrix表示的旋转。然后，.axis()方法用于获取该旋转向量的旋转轴，而.angle()方法用于获取旋转角度。接着，AngleAxisd(rotation_matrix).axis() * AngleAxisd(rotation_matrix).angle()部分将旋转向量的轴乘以旋转角度，这将得到一个旋转向量，其方向由旋转轴决定，大小由旋转角度决定。这个旋转向量被赋值给了extracted_rotation_vector。*/// 从欧式变换矩阵分解出旋转向量和平移向量Vector3d extracted_rotation_vector = AngleAxisd(rotation_matrix).axis() * AngleAxisd(rotation_matrix).angle();/* block<3,1>(0,3)是Eigen库中的一个函数，用于从矩阵中提取特定的块。在这里，block<3,1>(0,3)表示提取了从第0行开始，第3列开始的一个3x1的块，即欧氏变换矩阵的前三个元素（0, 1, 2行，3列），这通常是表示平移向量的部分。*/ Vector3d extracted_translation_vector = euclidean_transform_matrix.block<3,1>(0,3);// 输出欧式变换矩阵、提取的旋转向量和平移向量// 欧式变换矩阵std::cout << "\nEuclidean Transformation Matrix:\n" << euclidean_transform_matrix << std::endl;// 旋转向量std::cout << "Extracted Rotation Vector: " << extracted_rotation_vector.transpose() << std::endl;// 平移向量std::cout << "Extracted Translation Vector: " << extracted_translation_vector.transpose() << std::endl;return 0;
}