本文主要是介绍统计学习方法笔记-K近邻法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
k近邻法是一种基本分类与回归方法，这儿只讨论分类问题中的k近邻法。k近邻法输入为实例的特征向量，输出为实例的类别，可以取多类。
K近邻算法
简介：
给定一个训练数据集，对新输入的实例，在训练数据集中找到与其最近邻的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。
算法：
1、根据给定的距离度量，在训练集中找出实例x最邻近的k个实例，涵盖这k个实例的x的领域记作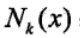 
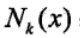
2、在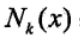 
中根据分类决策规则（如多数表决）决定x的类别y：
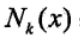中根据分类决策规则（如多数表决）决定x的类别y：
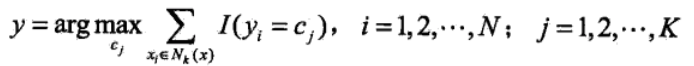
其中I()为指示函数，即yi = cj时，I()为1，否则为0
k近邻模型
模型：
特征空间中，对每个训练实例点xi，距离该点比其他点更近的区域，叫作单元。所有实例点的单元构成对特征区域的划分。最近邻法讲实例xi的类yi作为其单元中所有点的类标记。
距离度量：
特征空间中两个实例点的距离是两个实例点相似度的反映。k近邻法一般使用的距离是欧氏距离，但也可以是其他距离。
k值的选择：
选择较小的k值，学习的近似误差减小，但学习的估计误差会增大，预测结果对近邻的实例点非常敏感，如果近邻的实例点恰好是噪声，预测就会出错。也就是说k值减小，意味着模型变得复杂，更容易发生过拟合。
选择小的k值，可以减小估计误差，但是会增大近似误差，k值的增大意味着模型变得简单。
在应用中，k值一般去一个比较小的值，通常采用交叉验证法来选取最优k值。
分类决策规则：
k近邻法中分类决策规则往往是多数表决。误分类率是：
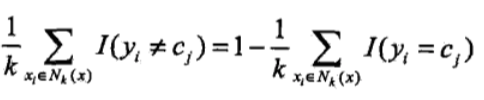
要使误分类率最小即经验风险最小，就得让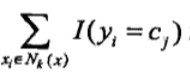 
最大，所以多数表决等价于经验风险最小。
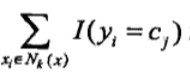最大，所以多数表决等价于经验风险最小。
kd树
构造kd树：
1、开始：构造根结点，根结点对应于包含T（T为训练数据集）的k维空间的超矩形区域。
选择x¹为坐标轴，以T中所有x¹的中位数为切分点，将根结点对应的超矩形区域切分成两个子区域，切分由通过切分点并与坐标轴x¹垂直的超平面实现。
由根结点生成深度为1的左、右子结点：
2、重复：对深度为j的结点，选择 x ( l ) 为切分的坐标轴，l = j(mod k) + 1，以该结点的区域中所有实例的x( l )坐标的中位数为切分点（如果是偶数个，也可以最中间二者选其一），将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并且与坐标轴x( l )垂直的超平面实现。
由该结点生成深度为j + 1的左、右子结点：左子结点对应坐标x( l )小于切分点的子区域，右子结点对应坐标x( l )大于切分点的子区域。
将落在切分超平面上的实例点保存在该结点。
搜索kd树：
1、在kd树中找出包含目标点x的叶结点：从根节点出发，递归向下访问kd树。若目标点x当前维的坐标小于切分点坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止。
（之所以上面这个过程没有判断等于（即目标点正好为某个父结点的特例），是因为单个维度等于不足以确定就是某个类，而目标点和训练点所有特征值相等的可能性太低，而单一特征值相等的可能性要高些，要是每出现某个纬度一样就对比所有特征值效率太低，所以干脆往右移，最终确定的一个叶结点。就算此时目标点正好是某个父节点甚至根节点这样的特例（可能性太低太低），最终也会找出这个父节点就是最近点，不会出现找出错误最近点的情况，总的来说不判断特殊情况利大于弊）
（我之前的观点：如果目标点当前维大于切分点坐标，且当前所在子结点只有左子结点并没有右子结点，那么就停留在当前结点。
这个观点有点问题，如果按照接下来的算法，这个观点不会在当前结点的区域下遍历找最近点，而是直接跳到父节点，所以具体实现还是得我找时间看kd树搜索算法的实现！）
2、以此叶结点为“当前最近点”
3、递归的向上回退，在每个结点执行以下操作：
a、如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例为“当前最近点”（父结点在这个时候进行距离比较）
b、当前最近点一定存在于该结点一个子结点对应的区域。检查该子结点的父结点的另一个子结点对应的区域是否有更近的点。具体的，检查另一个子结点对应的区域是否与以目标点为球心，以目标点与“当前最近点”的距离为半径的超球体相交。
如果相交，可能在另一个子结点对应的区域存在距目标点更近的点，移动到另一个子结点，接着，递归地进行最近邻搜索（自解释：如果这个子结点的度不为0，则从选择叶结点步骤开始，否则直接比较此节点保存的唯一实例点）；
如果不相交，向上回退。(子结树的所有点都不用比较了，这个时候效率就体现出来的)
4、当回到根节点时，搜索结束，最后的“当前最近点”即为x的最近邻点
这篇关于统计学习方法笔记-K近邻法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
