【GDOI2014模拟】​Pty爬山 题解+代码

本文主要是介绍【GDOI2014模拟】​Pty爬山 题解+代码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Description

在Pty学校附近，有一座名之为岳之麓的高山。Pty很喜欢和（哔——）一起爬山。
山的平面模型如下：
山由一个顶点集：A1,A2…An给定，保证Ai的x单调递增。我们将Ai和Ai+1之间连上线段，表示山的某一段。如下图所示：

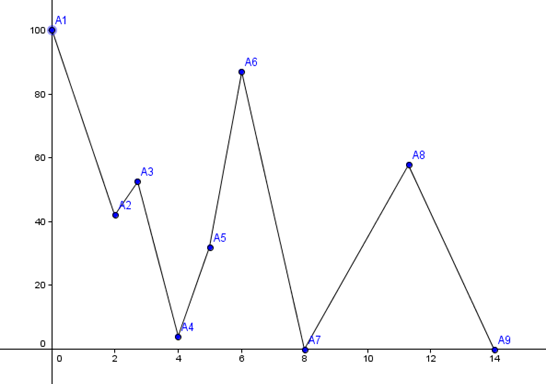
​Pty想要爬到这座山的最高的顶点，当两个顶点的高度相同时，我们认为x比较大的顶点要高一些。Pty不是盲人，所以他将会在爬山时采取一些策略，使得他能够尽量快的到达最高的顶点。
Pty从初始的顶点出发，往左右看去，他将朝他能够看到的最高的顶点方向走去。当走到每一个顶点时，他都会重新观察，如果这时看到的顶点比之前看到的顶点还要高，那么他将选择此时看到的顶点走去，直到他到达最高点为止。
例如上图中：Pty从A4点出发。他能够看到的最高点是A6，所以他将会向右侧走去。当他到达A5号点时，能够看到A1点比A6点更高，所以他会调转方向，向左侧走去。由于A1是最高的顶点，所以他将一直往左侧走，直到到达A1为止。
Pty想知道从每一个顶点出发，分别需要走过多少段才能到达最高点。例如上图中从A4出发需要走过5段才能到达最高点。

Input

第一行输入n，表示n个顶点。
接下来n行，每行两个整数xi, yi，表示第i个顶点的坐标。
输入保证xi单调递增。

Output

输出共n行：第i行表示从第i个顶点出发走到最高点需要经过多少步。

Sample Input

5
1 5
2 4
3 9
4 0
5 2

Sample Output

2
1
0
1
2

Data Constraint

30%的数据满足：n<= 100
60%的数据满足：n <= 50000
100%的数据满足：n<=200000, xi<=10^6, yi<= 10^6
请注意优化常数。

Solution

这题看似挺复杂，实际挺简单。

首先有个注意事项：在这题里，三点共线是可以看到的，这说明地球不是圆的。

分为几个小问
1、对于一个点，找到它左边和右边分别能看到的最高点（不包括自己）
这个问题可以通过斜率来做。如上面的图，A3到A4的边的斜率小于A4到A5的斜率，那么A3能看到A5，A5也能看到A3。对于A1，它能看到A3，而A3能看到A6，并且互相都是斜率一个比一个大，所以A1能看到A6，但是A1与A6连边的斜率大于A6与A8的斜率，所以A1就看不到A8了
code

fo(i,1,n) {L[i]=i-1;R[i]=i+1;down[i]=i+1;up[i]=i-1;}R[n]=n;L[1]=1;fd(i,n-2,1){for(;xl(i,R[i])<=xl(i,R[R[i]]);R[i]=R[R[i]]) if(R[i]==n) break;}fo(i,3,n){for(;xl(L[L[i]],i)<=xl(L[i],i);L[i]=L[L[i]]) if(L[i]==1) break;}

2、对于一个点，它往一个方向走，走到哪个点才会看到更高的点（不包括自己）
设f[a]表示a能看到的最高的点的高度，在求上一个问时可以同时求出f。
先做一个双向链表，1连2,2连3,3连4……
按f[a]从小到大排序（高度相同时，X坐标越小高度越小），按照排序后的顺序，高度从低到高的点依次做。这个点该往哪边走，双向链表中对应方向上与之相邻的点就是要找的点，然后把做过的点删掉即可。

现在我们想：一个点出发到最高点的距离，等不等于这个点走动过程中看到更高点后，再从这个点出发到达最高点的距离？答案是肯定的，那么
问题3：在知道上面的东西后，怎么求最终答案
把第二问求得的东西即点i在走动时看到更高的点向i连边，最后就会形成一棵树
code

fo(i,1,n) {if (a[L[i]].y>a[R[i]].y){f[i].x=a[L[i]].y;f[i].z=a[L[i]].x;}else{f[i].x=a[R[i]].y;f[i].z=a[R[i]].x;}f[i].y=i;}sort(f+1,f+n+1,cmp);fo(j,1,n)if (hi!=f[j].y){int i=f[j].y,x;if (a[L[i]].y>a[R[i]].y) putin(i,up[i],i-up[i]),x=up[i];else putin(i,down[i],down[i]-i),x=down[i];down[up[i]]=down[i];up[down[i]]=up[i];}

然后从最高点开始遍历，即可找到每个点到最高点应走的距离

Code

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define N 201000
using namespace std;
int n,L[N],R[N],up[N],down[N],last[N],next[N*10],data[N*10],to[N*10],tot=0,hi=0,ans[N],d[N*10];
bool bz[N];
struct note{int x,y,z;
};
note a[N],f[N];
double xl(int i,int j){return (a[i].y-a[j].y)*1.0/(a[i].x-a[j].x);
}
bool cmp(note x,note y)
{return (x.x<y.x)||(x.x==y.x && x.z<y.z);
}
void putin(int x,int y,int z){next[++tot]=last[y];last[y]=tot;to[tot]=x;data[tot]=z;
}
void bfs(int x)
{bz[x]=1;int i=0,j=1;d[1]=x;while (i<j){int k=d[++i];for(int l=last[k];l;l=next[l]){ans[to[l]]=ans[k]+data[l];d[++j]=to[l];bz[to[l]]=1;}}
}
int main()
{scanf("%d",&n);fo(i,1,n) {scanf("%d%d",&a[i].x,&a[i].y);if (a[i].y>=a[hi].y) hi=i;L[i]=i-1;R[i]=i+1;down[i]=i+1;up[i]=i-1;}down[n]=0;R[n]=n;L[1]=1;fd(i,n-2,1){for(;xl(i,R[i])<=xl(i,R[R[i]]);R[i]=R[R[i]]) if(R[i]==n) break;}fo(i,3,n){for(;xl(L[L[i]],i)<=xl(L[i],i);L[i]=L[L[i]]) if(L[i]==1) break;}fo(i,1,n) {if (a[L[i]].y>a[R[i]].y){f[i].x=a[L[i]].y;f[i].z=a[L[i]].x;}else{f[i].x=a[R[i]].y;f[i].z=a[R[i]].x;}f[i].y=i;}sort(f+1,f+n+1,cmp);fo(j,1,n)if (hi!=f[j].y){int i=f[j].y,x;if (a[L[i]].y>a[R[i]].y) putin(i,up[i],i-up[i]),x=up[i];else putin(i,down[i],down[i]-i),x=down[i];down[up[i]]=down[i];up[down[i]]=up[i];}ans[hi]=0;bfs(hi);fo(i,1,n) printf("%d\n",ans[i]);
}

这篇关于【GDOI2014模拟】​Pty爬山 题解+代码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---