本文主要是介绍POJ 1179 Polygon(动态规划:类似环形石子合并),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
点击打开链接
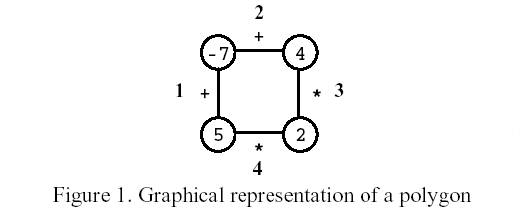
题意:给出一个多边形,切断某一条边,求出所有边合并后的最大值。
注意:最大值可能由最小值得来(负负得正)!所以要用两个dp数组维护。
第一次提交:WA,因为dMin[i][j] = getMin ( dMin[i][j], 那里直接复制前面的dMax[i][j] = getMax。
dMax没有改成dMin。。。。
第二次:PE,因为判断是否为第一个答案时用:i == 0来判断……
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int MAX_N = 51;
const int INF = 0x3f3f3f3f;
int n;
int a[MAX_N * 2];
char e[MAX_N * 2];
int dMax[MAX_N * 2][MAX_N * 2];
int dMin[MAX_N * 2][MAX_N * 2];inline int getMax ( int a, int b, int c, int d , int e )
{return max ( max ( max ( a, b ), max ( c, d ) ) , e );
}inline int getMin ( int a, int b, int c, int d , int e )
{return min ( min ( min ( a, b ), min ( c, d ) ) , e );
}void solve()
{//initfor ( int i = 0; i <= 2 * n; i++ ){for ( int j = 0; j <= 2 * n; j++ ){if ( i == j ){dMax[i][i] = dMin[i][i] = a[i];}else{dMax[i][j] = -INF;dMin[i][j] = INF;}}}for ( int len = 1; len < n; len++ ){for ( int i = 0; i + len < 2 * n; i++ ){int j = i + len;for ( int k = i; k < j; k++ ){if ( e[k + 1] == 't' ) //plus{dMax[i][j] = max ( dMax[i][j], dMax[i][k] + dMax[k + 1][j] );dMin[i][j] = min ( dMin[i][j], dMin[i][k] + dMin[k + 1][j] );}else //multi{//最大值可能由最小值得来(负负得正)dMax[i][j] = getMax ( dMax[i][j],dMax[i][k] * dMax[k + 1][j],dMin[i][k] * dMin[k + 1][j],dMax[i][k] * dMin[k + 1][j],dMin[i][k] * dMax[k + 1][j] );dMin[i][j] = getMin ( dMin[i][j],dMax[i][k] * dMax[k + 1][j],dMin[i][k] * dMin[k + 1][j],dMax[i][k] * dMin[k + 1][j],dMin[i][k] * dMax[k + 1][j] );}}}}int ans = -INF;for(int i = 0; i < n; i++){ans = max(ans, dMax[i][i+n-1]);}printf("%d\n", ans);bool first = true;for(int i = 0; i < n; i++){if(dMax[i][i+n-1] == ans){printf(first ? "%d" : " %d", i+1);first = false;}}printf("\n");
}int main()
{//freopen ( "in.txt", "r", stdin );scanf ( "%d\n", &n );for ( int i = 0; i < n; i++ ){scanf ( "%c %d", e + i, a + i );getchar();e[i + n] = e[i];a[i + n] = a[i];}solve();return 0;
}这篇关于POJ 1179 Polygon(动态规划:类似环形石子合并)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





