本文主要是介绍06 实现数值的整数次方,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
本博文部分图片, 思路来自于剑指offer 或者编程珠玑
问题描述
思路
书中给出了两种思路
设定输入的基数为base, 幂数为exp
思路一 : 构造一个循环, exp次相乘得到结果
思路二 : 在第一种思路的前提下面, 对于输入进行检查, 增加处理负数的情况 [鲁棒性]
思路三 : 在第二种思路的基础上面, 优化求幂的过程, 将pow(3, 7) –decompose–> pow(3, 4) * pow(3, 2) * pow(3, 1), 缓存base的整数次方的结果, 可以节省很多开销
参考代码
/*** file name : Test27PowImp.java* created at : 11:24:06 AM Jun 5, 2015* created by 970655147*/package com.hx.test04;public class Test27PowImp {// 实现pow方法public static void main(String []args) {double base = 3;int exp = 7;double res = pow01(base, exp);Log.log(res);res = pow02(base, exp);Log.log(res);res = pow03(base, exp);Log.log(res);}// 只考虑了exp为正数的情况, 所以不全面, 并且没有考虑base为0的输入public static double pow01(double base, int exp) {double res = 1.0;for(int i=0; i<exp; i++) {res *= base;}return res;}// 考虑了exp为正负数, base可能为0的输入public static double pow02(double base, int exp) {if(eq(base, 0.0) ) {return 1.0;}boolean isPos = true;if(exp < 0) {exp = -exp;isPos = false;}double res = 1.0;for(int i=0; i<exp; i++) {res *= base;}if(! isPos) {res = 1/ res;}return res;}// 考虑了exp为正负数, base可能为0的输入// 优化求幂的过程public static double pow03(double base, int exp) {if(eq(base, 0.0) ) {return 1.0;}boolean isPos = true;if(exp < 0) {exp = -exp;isPos = false;}double res = powUnsigned(base, exp);if(!isPos) {res = 1/ res;}return res;}// 确保exp为正 计算通常情况下的base^exp// 比循环相乘更优 比如 : 2^32 = (2^16)^2 = ((2^8)^2)^2 = (((2^4)^2)^2)^2 = ((((2^2)^2)^2)^2)^2// 乘法的话 会计算2*2*2*....*2[32个2]public static double powUnsigned(double base, int exp) {int tmp = exp;int higestOneBit = -1;int res = 1, baseTmp = (int ) base;if(! eq(lastBase, base)) {powCache.clear();lastBase = base;}while(tmp > 0) {higestOneBit = Integer.highestOneBit(tmp);res = res * getResForHigestOneBit(baseTmp, higestOneBit);tmp -= higestOneBit;}return res;}// 计算base的 higestOneBit, 其中higestOneBit是2的n次方["整数"]// 存在缓存static double lastBase = -1;static Map<Integer, Integer> powCache = new HashMap<Integer, Integer>();private static int getResForHigestOneBit(int base, int higestOneBit) {if(higestOneBit == 1) {return base;}if(powCache.containsKey(higestOneBit)) {return powCache.get(higestOneBit);} else {int half = getResForHigestOneBit(base, (higestOneBit >> 1) );int res = half * half;powCache.put(higestOneBit, res);return res;}}// 判断两个浮点数 是否相等[区间判别]static double minDiff = 0.0000001d;private static boolean eq(double param01, double param02) {if(Math.abs(param01 - param02) < minDiff) {return true;}return false;}}
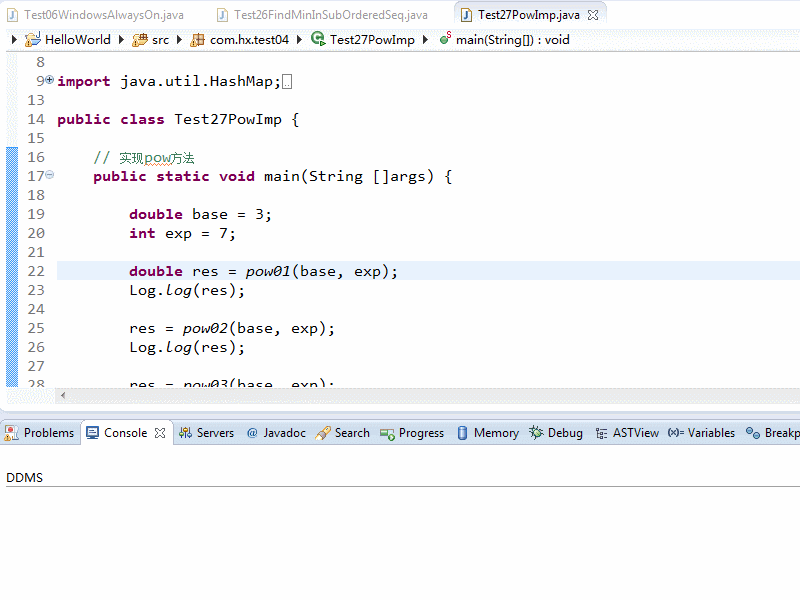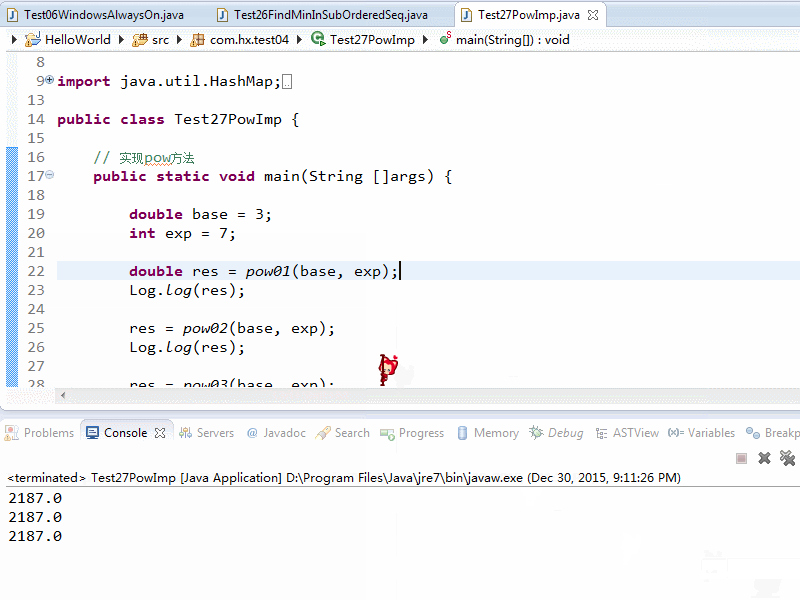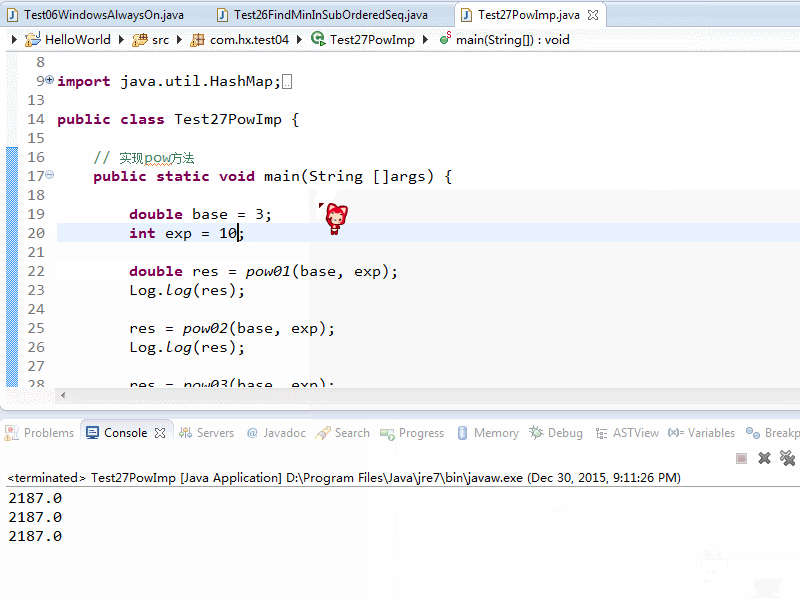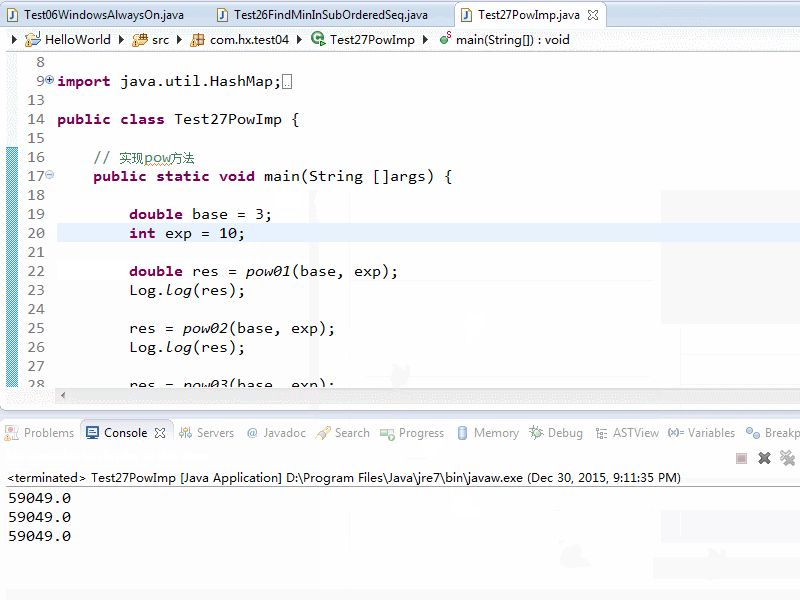
效果截图
总结
是否是对算法三的计算优化有一种叹为观止的感脚?, 对于固定基数[base]的场景, 只用缓存n个pow的结果, 就能够计算base为基数, exp范围为[0-2^(n+1) ) 之间的数据, 而且灰常快
注 : 因为作者的水平有限,必然可能出现一些bug, 所以请大家指出!
这篇关于06 实现数值的整数次方的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!