HILL密码

本文主要是介绍HILL密码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

 

一：简介

  Hill密码又称希尔密码是运用基本矩阵论原理的替换密码，属于多表代换密码的一种，由L e s t e r S . H i l l Lester S. HillLesterS.Hill在1929年发明。

二：原理

  1.对于每一个字母，我们将其转化为对应的数字，一般来说我们使用的是 A AA 对应的 0 ，B对应的 1然后一次类推，当然你也可以自己指定一个字母表，然后一一对应。
  2.我们将明文转化为一个1维的向量 （即：1 × n 的矩阵）。
  3.然后我们将这个1维的向量和一个 n × n 的密钥矩阵相乘，得到一个1维的向量，然后对这个矩阵模上26。
  4.然后再通过字母表将这个n维矩阵转化为密文。
 

解密 的话只需要将密文乘上密文矩阵的逆矩阵就好啦，Hill 密码能较好地抵抗统计分析法，对抗唯密文攻击的强度较高，但易受到已知明文攻击。破译的难度也会随着矩阵的阶数规模变大变得难以破解。

三：举例

我们的明文为：ACM，我们想将其加密，我们得到的一个密钥矩阵如下：

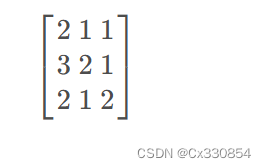
1. 我们将明文转为一个1维向量：

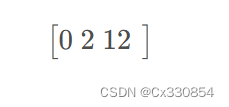
     2.对两个矩阵做一个乘法

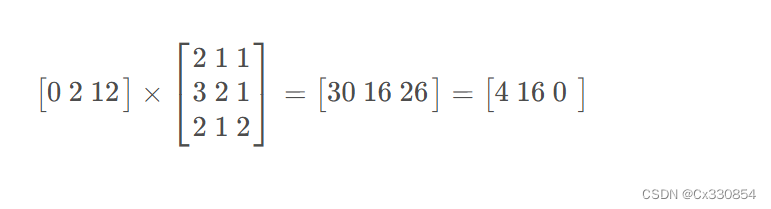
     3.将新得到的1维向量按照字母表转化为密文：

python代码实现如下：

#include<bits/stdc++.h>
using namespace std;
#define N 100
#define mod 26
struct Matrix{int n,m;int mp[N][N];void init(int n,int m) {this->n = n;this->m = m;for(int i = 0;i <= n; ++i) for(int j = 0;j <= m; ++j)mp[i][j] = 0;}
};Matrix mult(Matrix L,Matrix R) {//乘法if(L.m != R.n) return L;Matrix M;M.init(L.n,R.m);for(int i = 0;i < L.n; ++i) {for(int j = 0;j < R.m; ++j){for(int k = 0;k < L.m; ++k) {M.mp[i][j] = (M.mp[i][j] + L.mp[i][k] * R.mp[k][j]) % mod;}}}return M;
}void HIll(){Matrix a,b;string S;cout<<"请输入需要加密的明文"<<endl;cin>>S;transform(S.begin(),S.end(),S.begin(), ::toupper);int len = S.size();cout<<"请输入"<<len<<"X"<<len<<"的密钥矩阵"<<endl;a.init(len,len);b.init(1,len);for(int i = 0;i < len; ++i)for(int j = 0;j < len; ++j)scanf("%d",&a.mp[i][j]);for(int i = 0;i < len; ++i) b.mp[0][i] = int(S[i] - 'A');for(int i = 0;i < len; ++i) cout<<b.mp[0][i]<<" \n"[i == len-1];Matrix c = mult(b,a);string ans = "";for(int i = 0;i < len; ++i)ans += char('A' + c.mp[0][i]);cout<<"加密后的密文为：\n"<<ans<<endl;
}int main()
{HIll();return 0;
}
/*
ACM
2 1 1
3 2 1
2 1 2ans = EQA
----------------
ACT
6 24 1
13 16 10
20 17 15	ans = QRT
----------------
cyber
10 5 12 0 0
3 14 21 0 0
8 9 11 0 0
0 0 0 11 8
0 0 0 3 7
ans = WRTRV
*/

运行结果：

 

矩阵求逆原理：（Gauss-Jordan）高斯消元法求逆矩阵（含C/C++实现代码）-CSDN博客

（本人不才，请看别人的）

这篇关于HILL密码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---