【控制实践——二轮平衡车】【三】基于PID的直立控制

本文主要是介绍【控制实践——二轮平衡车】【三】基于PID的直立控制，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

---

系列博客

【控制实践——二轮平衡车】【一】运动分析及动力学建模
【控制实践——二轮平衡车】【二】实物设计和开源结构&代码
【控制实践——二轮平衡车】【三】基于PID的直立控制

前言

在前面两篇博客中，分别对二轮平衡车的动力学进行分析，并且制作实物用于验证算法可行性。
后面的博客将采用不同的控制算法来实现二轮平衡车的控制。算法的实现代码将保存在开源仓库的不同分支中。

直立运动分析

在第一篇的博客中，对不同坐标系下的运动过程进行受力分析，得到了两个描述二轮平衡车的运动公式。

• 惯性系下（以地面为参考系）
  $$({\mathbf{m}}_{\mathbf{p}}+{\mathbf{m}}_{\mathbf{w}}){\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}={\mathbf{m}}_{\mathbf{p}}\mathbf{l}\stackrel{\cdot \cdot }{\mathbf{\alpha }}\mathbf{cos\alpha }-{\mathbf{m}}_{\mathbf{p}}\mathbf{l}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\mathbf{sin\alpha }\text{\hspace{1em}(1)}$$
• 非惯性系下（以车轮中心为参考系）
  $$\mathbf{J}\stackrel{\cdot \cdot }{\mathbf{\alpha }}={\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }+{\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}\mathbf{lcos\alpha }\text{\hspace{1em}(2)}$$
• 不同角度${\dot{\mathbf{\alpha }}}_0$，${\mathbf{\alpha }}_0$下，二轮平衡车的角度、角速度、角加速度变化公式
  $$(\mathbf{J}-\frac{{\mathbf{m}}_{\mathbf{p}}^2{\mathbf{l}}^2\mathbf{co}{\mathbf{s}}^2\mathbf{\alpha }}{{\mathbf{m}}_{\mathbf{p}}+{\mathbf{m}}_{\mathbf{w}}})\stackrel{\cdot \cdot }{\mathbf{\alpha }}={\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }-\frac{{\mathbf{m}}_{\mathbf{p}}^2{\mathbf{l}}^2\mathbf{sin\alpha cos\alpha }}{{\mathbf{m}}_{\mathbf{p}}+{\mathbf{m}}_{\mathbf{w}}}{\stackrel{\cdot }{\mathbf{\alpha }}}^2\text{\hspace{1em}(3)}$$
  因为一定知道了初始状态，就可以计算代入等式右边得到角加速度，进而计算出新的角速度和角度，周而复始。

分析三个公式，哪个公式适合用来做控制分析呢。

• 公式（1） 描述的是转动$\mathbf{\alpha }$对轮子运动${\mathbf{x}}_{\mathbf{w}}$的影响，此时轮子是被动的一方。即
  $$\mathbf{\alpha }\to {\mathbf{x}}_{\mathbf{w}}$$
• 公式（2） 描述的是轮子运动${\ddot{\mathbf{x}}}_{\mathbf{w}}$对转动$\ddot{\mathbf{\alpha }}$的影响，进而影响角度$\mathbf{\alpha }$。即
  $${\ddot{\mathbf{x}}}_{\mathbf{w}}\to \ddot{\mathbf{\alpha }}$$
• 公式（3） 描述的是初始角度${\mathbf{\alpha }}_0$和初始角速度${\dot{\mathbf{\alpha }}}_0$对自身转动的影响，即自身角度转动的演化趋势。

显然，在直立控制时，希望控制的是平衡车的转动运动，并且需要有一个可控量来完成，因此只有公式（2）适合作为被控对象模型。即通过控制轮子运动来控制转动运动，正好符合二轮平衡车的工作原理。

基于PID控制器的直立控制

设状态向量为$\mathbf{X}=\left[\begin{array}{c}\mathbf{\alpha }\\ \dot{\mathbf{\alpha }}\end{array}\right]$，系统输入为$\mathbf{U}={\ddot{\mathbf{x}}}_{\mathbf{w}}$，系统状态方程为：
$$\dot{\mathbf{X}}=\left[\begin{array}{cc}0& 1\\ {\mathbf{m}}_{\mathbf{p}}\mathbf{glsin}& 0\end{array}\right]\mathbf{X}+\left[\begin{array}{c}0\\ {\mathbf{m}}_{\mathbf{p}}\mathbf{lcos\alpha }\end{array}\right]\mathbf{U}\text{\hspace{1em}(4)}$$
列出状态方程的目的，主要是为了能够直观地描述直立运动的状态转移过程，帮助理解控制设计的原理。下面采用PID控制器进行控制设计。

角度环控制

• 从状态方程可以看出，角度的变化只受到角速度的影响，即：
  $$\frac{\mathbf{d\alpha }}{\mathbf{dt}}=\dot{\mathbf{\alpha }}\text{\hspace{1em}(5)}$$
  设角度期望为${\alpha }_{ref}$，则角度误差$erro{r}_{\alpha }$为：
  $$erro{r}_{\alpha }={\mathbf{\alpha }}_{\mathbf{ref}}-\mathbf{\alpha }\text{\hspace{1em}(6)}$$
  因此在做角度的控制的时候，将$\dot{\mathbf{\alpha }}$作为系统输入${\mathbf{U}}_{\alpha }$，并且根据PID控制器的控制律可以得到：
  $${\mathbf{U}}_{\alpha }=K_{p}erro{r}_{\alpha }+K_i\int erro{r}_{\alpha }dt+K_d\ast \frac{derro{r}_{\alpha }}{dt}\text{\hspace{1em}(7)}$$
  得到的角度控制律${\mathbf{U}}_{\alpha }$原本是直接作用到被控对象里来影响角度$\mathbf{\alpha }$，但是被控对象无法直接决定角速度的数值，因此此处的控制律${\mathbf{U}}_{\alpha }$即为期望的角速度数值${\dot{\mathbf{\alpha }}}_{\mathbf{ref}}$。即：
  $${\dot{\mathbf{\alpha }}}_{\mathbf{ref}}={\mathbf{U}}_{\alpha }\text{\hspace{1em}(8)}$$

角速度控制

• 从状态方程可以看出，角速度的变化受到了角加速度（重力分量${\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }$和惯性力分量${\mathbf{m}}_{\mathbf{p}}\mathbf{lcos\alpha }{\ddot{\mathbf{x}}}_{\mathbf{w}}$）影响。
  $$\frac{\mathbf{d}\dot{\mathbf{\alpha }}}{\mathbf{dt}}=\ddot{\mathbf{\alpha }}=\frac{1}{\mathbf{J}}({\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha }+{\mathbf{m}}_{\mathbf{p}}{\stackrel{\cdot \cdot }{\mathbf{x}}}_{\mathbf{w}}\mathbf{lcos\alpha })\text{\hspace{1em}(9)}$$
  角速度误差$erro{r}_{\dot{\alpha }}$为：
  $$erro{r}_{\dot{\alpha }}={\dot{\mathbf{\alpha }}}_{\mathbf{ref}}-\dot{\mathbf{\alpha }}\text{\hspace{1em}(10)}$$
  同样在做角速度的控制时，将$\ddot{\mathbf{\alpha }}$作为系统输入${\mathbf{U}}_{\dot{\alpha }}$，并且根据PID控制器的控制律可以得到：
  $${\mathbf{U}}_{\dot{\alpha }}=K_{p}erro{r}_{\dot{\alpha }}+K_i\int erro{r}_{\dot{\alpha }}dt+K_d\ast \frac{derro{r}_{\dot{\alpha }}}{dt}\text{\hspace{1em}(11)}$$
  同样，可以得到：
  $${\ddot{\mathbf{\alpha }}}_{\mathbf{ref}}={\mathbf{U}}_{\dot{\alpha }}\text{\hspace{1em}(12)}$$
  根据公式（9） 可以得到期望的轮子加速度${\ddot{\mathbf{x}}}_{\mathbf{w},\mathbf{ref}}$
  $${\ddot{\mathbf{x}}}_{\mathbf{w},\mathbf{ref}}=(\mathbf{J}{\ddot{\mathbf{\alpha }}}_{\mathbf{ref}}-{\mathbf{m}}_{\mathbf{p}}\mathbf{glsin\alpha })/{\mathbf{m}}_{\mathbf{p}}\mathbf{lcos\alpha }\text{\hspace{1em}(13)}$$

总结

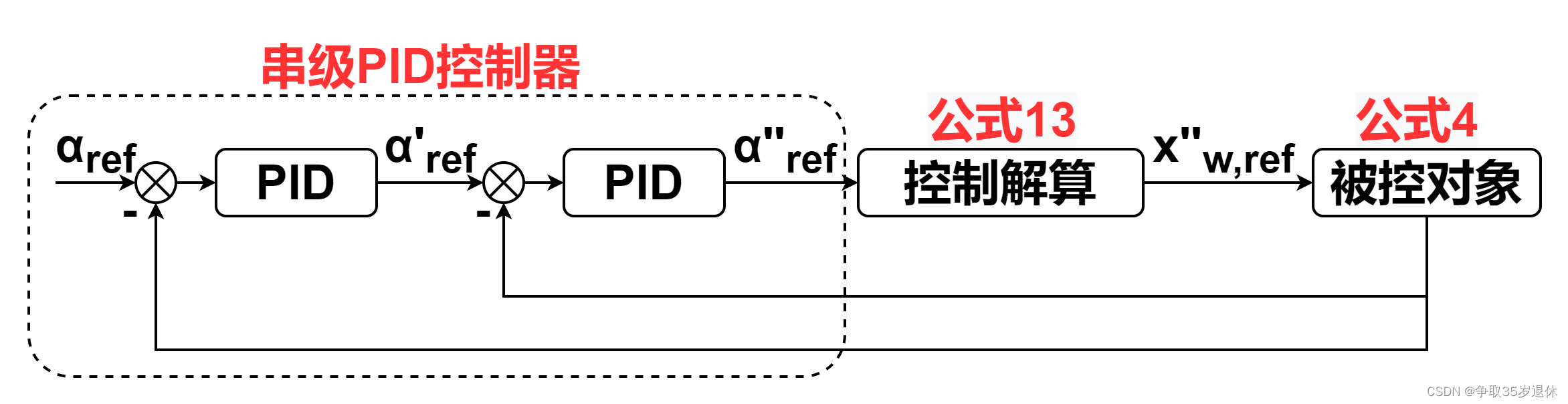
前面的角度角速度控制，其实就是很常见的串级PID控制器，故意拆成两部分来分析，是为了更清晰地展示串级PID控制器的原理，以及为后续一些算法的变种做铺垫，即，角度控制用一种控制算法，角速度控制用另外的算法是否也可行？

• 直立控制的框图：
  
• $matlab$ 仿真
  仿真参数如下：
  $m=0.857kg$
  $g=9.8m/s^2$
  $l=0.05m$
  $J=0.0021kg\cdot m^2$
  $T=0.002s$
  $K{p}_{out}=5，K{i}_{out}=0.1，K{d}_{out}=0$
  $K{p}_{in}=100，K{i}_{in}=1，K{d}_{in}=0$

这些参数是第二篇博客平衡车的实物参数，以及控制参数也与实际的控制参数一致

T = 0.002;
%离散时间
n = 10000;
%仿真步数
m = 0.857;
%平衡车重量，单位kg
g = 9.8;
%重力加速度，单位m/s2
l = 0.05;
%轮子中心到质心距离，单位m
J = m*l*l;
%转动惯量
kp_out = 5;
ki_out = 0.1;
kd_out = 0;
%角度pid参数
kp_in = 100;
ki_in = 1;
kd_in = 0;
%角速度pid参数a_ref = zeros(n,1);
%角度期望，单位°
da_ref = zeros(n,1);
%角速度期望，单位rad/s
dda_ref = zeros(n,1);
%角加速度期望，单位rad/s2
u = zeros(n,1);
%系统输入，即轮子的加速度，单位m/s2a = zeros(n,1);
%角度状态，单位°
da = zeros(n,1);
%角速度状态，单位rad/s
dda = zeros(n,1);
%角加速度状态，单位rad/s2
time = zeros(n,1);
%时间轴a_integral = 0;
%角度误差积分
da_integral = 0;
%角速度误差积分
a_last_error = 0;
%角度上次误差
da_last_error = 0;
%角速度上次误差
for i = 1:ntime(i) = (i-1)*T;a_ref(i) = 10 * sin(time(i));% --------------------------- 仿真计算 ---------------------------%a_error = a_ref(i) - a(i);%角度误差a_integral = a_integral + a_error;%积分a_diff = (a_error - a_last_error)/T;%微分a_output = kp_out * a_error + ki_out * a_integral * T + kd_out * a_diff;%角度PID计算,对应公式7% --------------------------- 角度环 ---------------------------%da_ref(i) = a_output;%角速度期望da_error = da_ref(i) - da(i);%角速度误差da_integral = da_integral + da_error;%积分da_diff = (da_error - da_last_error)/T;%差分da_output = kp_in * da_error + ki_in * da_integral * T + kd_in * da_diff;%角速度PID计算,对应公式11  % --------------------------- 角速度环 ---------------------------%dda_ref(i) = da_output;%角加速度期望u(i) = (J*dda_ref(i) - m*g*l*sin(a(i)/180*pi)) / (m*l*cos(a(i)/180*pi));%计算系统输入,对应公式13% --------------------------- 控制解算 ---------------------------%if i == nbreak;enddda(i) = (m*g*l*sin(a(i)/180*pi) + m*l*cos(a(i)/180*pi)*u(i)) / J; %状态方程，对应公式2da(i+1) = da(i) + dda(i) * T;%角速度计算a(i+1) = a(i) + da(i) * T / pi * 180;%角度计算% --------------------------- 被控对象 ---------------------------%
endfigure(1);
subplot(2,2,1);
plot(time,a,'r',time,a_ref,'g');
title('角度响应曲线');
legend('角度','角度期望');
xlabel('time/s');
ylabel('角度/°');
subplot(2,2,2);
plot(time,da,'r',time,da_ref,'g');
title('角速度响应曲线');
legend('角速度','角速度期望');
xlabel('time/s');
ylabel('rad/s');
subplot(2,2,3);
plot(time,dda,'r',time,dda_ref,'g');
title('角加速度曲线');
legend('角加速度','角加速度期望');
xlabel('time/s');
ylabel('rad/s^2');
subplot(2,2,4);
plot(time,u,'r');
title('系统输入曲线');
legend('U');
xlabel('time/s');
ylabel('m/s^2');

仿真结果如下：

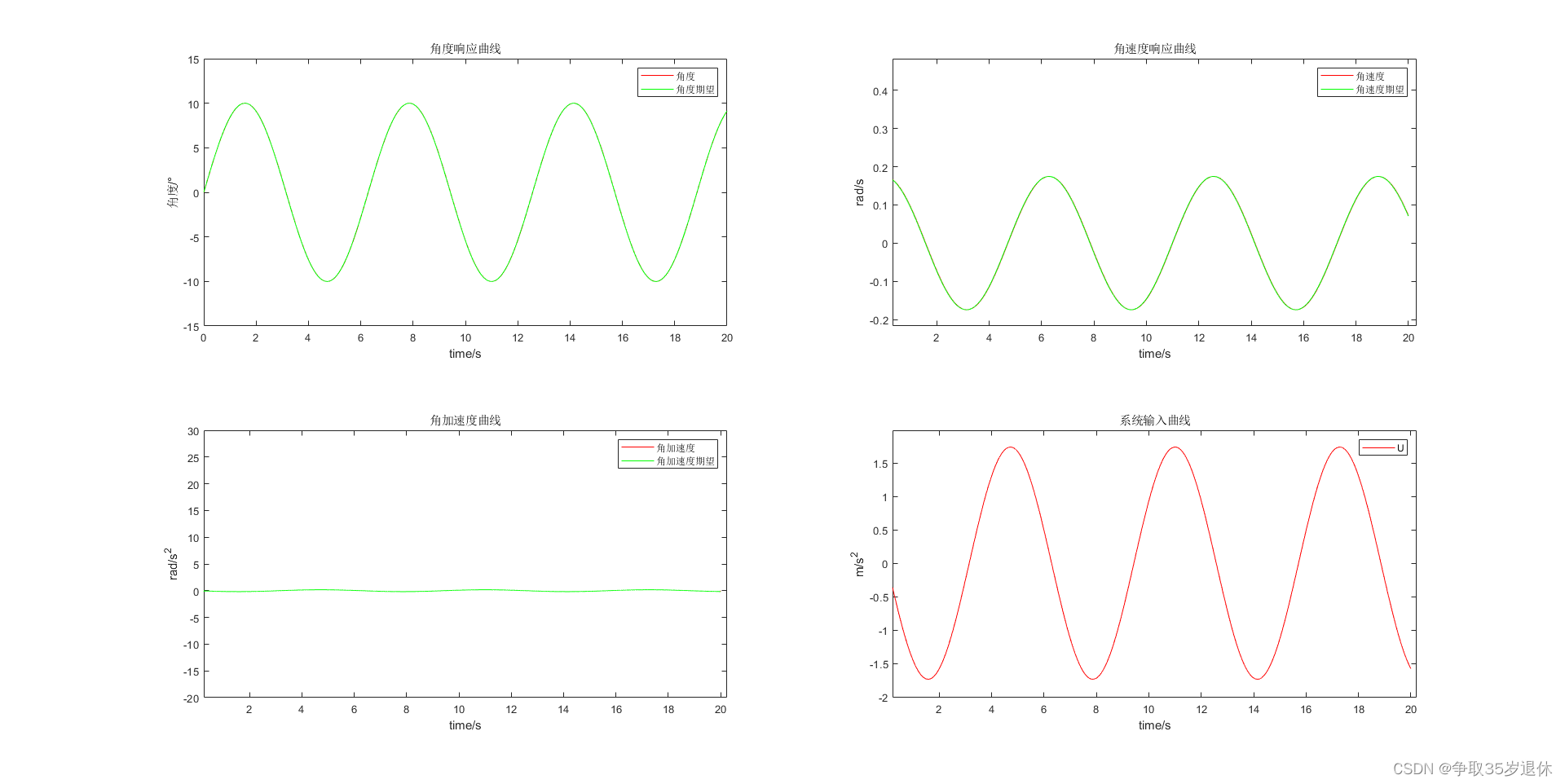
这里所用到的控制参数与实际使用的参数一致，有兴趣的同学可以去开源的控制代码里查看，代码在control.c文件中

电机转速的控制

前言

在直立控制中，采用的系统输入$\mathbf{U}$是电机轮子的加速度${\ddot{\mathbf{x}}}_{\mathbf{w}}$，因此实现平衡车直立的关键因素就是控制电机实现我们期望的运动，对电机的转速控制具有十分重要的意义。

电机转速控制

由于不同的电机转速的转速控制方式不同，因此这篇博客仅给出转速控制的一些思路，不做仿真和模型讨论。

电机转速控制的关键是获取电机的当前转速信息，常用的传感器有编码器，光电传感等。

而对于不同类型的电机采用的控制算法也不同。

• 对于直流驱动的电机来说，通常采用增量式PID控制。
• 对于带有FOC的无刷电机来说，通常采用位置式PID控制。

以上是个人经验所给出的建议，仅供参考。

无论以何种方式，在实现电机转速控制后，需要根据直立控制的解算结果，来得到当前的期望转速${\dot{\mathbf{x}}}_{\mathbf{w},\mathbf{ref}}$，即满足以下关系：
$${\dot{\mathbf{x}}}_{\mathbf{w},\mathbf{ref}}(k+1)={\dot{\mathbf{x}}}_{\mathbf{w}}(k)+{\ddot{\mathbf{x}}}_{\mathbf{w},\mathbf{ref}}(k)\ast T\text{\hspace{1em}(14)}$$
其中，$T$为离散周期，$k$为时刻序号。

最后，再将公式（14）计算得到的期望电机转速传入电机转速控制器中，即可完成整个平衡车的控制周期。即完整的控制框图为：

结语

实践是检验真理的唯一标准，看懂原理的同时也需要多实践。
最后再贴一下开源的代码按需自取：https://gitee.com/HaveALitttleSao/balance_car_control_code
放一下我个人调试的效果视频

• 俯视角度

• 侧面角度

以防有人说我把平衡车固定死造假 \doge

这篇关于【控制实践——二轮平衡车】【三】基于PID的直立控制的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---