条件熵，信息增益（互信息）与特征选择

本文主要是介绍条件熵，信息增益（互信息）与特征选择，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一定要先搞清楚什么是信息量，什么是信息熵。参考博文：https://blog.csdn.net/u010916338/article/details/91127242

一，什么是信息量？

简言之，就是把信源看做是一个随机变量。消息（信号）就是随机变量的取值，比如a1，a2···an。信息就是这些随机变量的不确程度（发生概率越低，不确定性越大），公式如下。为什么写成这样呢？原因有二。第一：概率和信息量（不确定性）是反比例关系；第二，当事件发生概率为1的时候，信息量为0。

注：信息量描绘的是一个随机变量的取值，a1有a1的信息量，a2有a2的信息量。

即信息量是对某一事件的不确定性的度量。

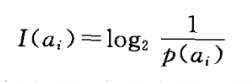
二，什么是信息熵 ？

接着上面，如何描绘随机变量的所有取值的信息量呢？就是求随机变量的期望。即求信息量的均值。

注：信息熵是对整个随机变量的不确定性的度量。

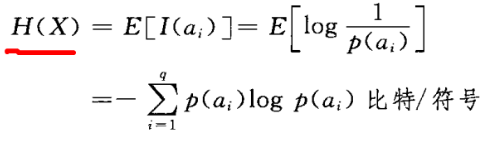
三，什么是信息增益（互信息）？

3.1  条件熵

先得搞清楚什么是条件熵，公式如下：

 

直接看公式，摸不到头脑，我们直接引入一个案例，结合案例很容易就理解了。

3.2  案例：哪个特征对QQ用户是否流失影响较大？

数据如下表所示，代表QQ用户是否流失。uin表示用户id；gender表示用户性别；act_info表示用户活跃度；is_lost表示用户是否流失，是标签值。

 

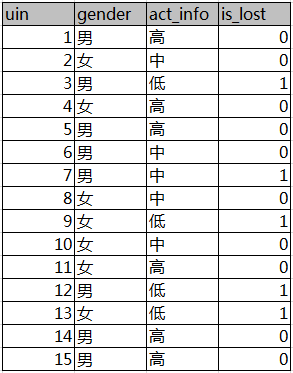
需求：性别和活跃度两个特征，哪个对用户流失影响更大？

数据归纳之后如下表所示，其中positive为正样本（已流失），negative为负样本（未流失）。

 

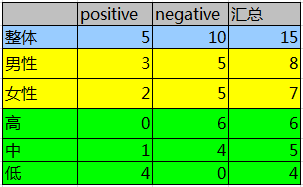
3.3  计算整体熵：

 整体熵： 

3.4  计算性别特征的条件熵，以及性别特征的信息增益

任意过来一个用户，猜测是已流失还是未流失，设为随机变量Y。

任意过来一个用户是男性或者是女性，设为随机变量X。

任意过来一个用户是男性，设为事件x1；

任意过来一个用户是女性，设为事件x2；

随机变量X的概率空间为： 

（1）男性条件熵：

（2）女性条件熵：

（3）性别条件熵：

                

                

（4）性别信息增益：

 

 3.5  计算活跃度特征的条件熵，以及活跃度特征的信息增益

任意过来一个用户，猜测是已流失还是未流失，设为随机变量Y。

任意过来一个用户活跃度是高，中或者低，设为随机变量X。

任意过来一个用户活跃度高，设为事件x1；

任意过来一个用户活跃度中，设为事件x2；

任意过来一个用户活跃度低，设为事件x3；

随机变量X的概率空间为： 

（1）活跃度高条件熵：

（2）活跃度中条件熵：

（3）活跃度低条件熵：

（4）活跃度条件熵：

                

                

（5）活跃度信息增益：

 

四，综述 

活跃度的信息增益比性别的信息增益大，也就是说，活跃度对用户流失的影响比性别大。

在做特征选择或者数据分析的时候，我们应该重点考察活跃度这个指标。

什么意思？

假如原来没有性别和活跃度这两个维度，后来活跃度这个维度的加入会比性别维度的加入导致整体信息熵提升的更多。

参考博文：https://blog.csdn.net/it_beecoder/article/details/79554388

这篇关于条件熵，信息增益（互信息）与特征选择的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---