2.1专题
2.1/5.1和7.1声道系统有什么区别? 音频声道的专业知识科普
《2.1/5.1和7.1声道系统有什么区别?音频声道的专业知识科普》当设置环绕声系统时,会遇到2.1、5.1、7.1、7.1.2、9.1等数字,当一遍又一遍地看到它们时,可能想知道它们是什... 想要把智能电视自带的音响升级成专业级的家庭影院系统吗?那么你将面临一个重要的选择——使用 2.1、5.1 还是
【2.1 深度学习中的感知机是什么】
2.1 深度学习中的感知机是什么 深度学习是机器学习的一个分支,它模拟人脑的工作方式来处理数据,尤其是通过神经网络的结构来自动提取数据的特征并进行分类、回归或其他复杂的任务。在深度学习的早期发展中,许多基础概念和模型为后续的复杂网络奠定了基础。其中,**感知机(Perceptron)**是一个非常重要的基础模型,它实际上是神经网络和深度学习的前身之一。 感知机的基本概念 感知机是一种二分
【AI大模型应用开发】2.1 Function Calling连接外部世界 - 入门与实战(1)
Function Calling是大模型连接外部世界的通道,目前出现的插件(Plugins )、OpenAI的Actions、各个大模型平台中出现的tools工具集,其实都是Function Calling的范畴。时下大火的OpenAI的GPTs,原理就是使用了Function Calling,例如联网检索、code interpreter。 本文带大家了解下Function calling,看
2.1ceph集群部署准备-硬件及拓扑
硬件配置及建议 时至今日,ceph可以运行在各种各样的硬件平台上,不管是传统的x86架构平台(intel 至强系列、基于amd的海光系列等),还是基于arm的架构平台(比如华为鲲鹏),都可以完美运行ceph集群,展现了其强大的适应能力。 ceph的不同组件对硬件的需求有些许不同,下面是官方推荐的硬件要求: 组件资源最低配置要求OSD处理器最少1 core每200-500 MB/s最少1 co
TokuDB7.5.7-2.1使用TokuDB的系统和硬件需求v1
1 操作系统需求 TokuDB到目前位置只支持64位的Linux系统(所以现在不支持在window上编译运行) 2 硬件需求 内存:至少1G;如果想较好性能,建议2G以上。 外存:建议为数据目录(tokudb_data_dir)和日志目录(tokudb_log_dir)配置足够大的存储空间。
个人旅游网(2.1)——使用阿里云在springboot项目中发送短信
文章目录 一、背景介绍二、详细步骤2.1、申请资质2.2、申请签名2.3、申请模板2.4、申请accessKey秘钥对2.5、SDK的使用[!]2.5.1、项目中导入依赖2.5.2、发短信的工具类 一、背景介绍 验证码发送背后的功能原理图: 想要在项目中实现上述发送验证码的功能,就需要了解以下步骤。 二、详细步骤 阿里云短信服务 一个短信一般分成成两部分:签名、模板
2.1 程序设计语言与概述
以下程序设计语言中,( )更适合用来进行动态网页处理。 A. HTML B. LISP C. PHP D. JAVA/C++ 正确答案是 C。 解析 HTML:静态网页 LISP:一种基于入演算的函数式编程语言 PHP:混合了C、Java、Perl以及PHP自创的语法。 它可以比CGl或者Perl更快速地执行动态网页。 引用调用方式下进行函数调用,是将( )。 A. 实参的值传递给形参
2.1概率统计的世界
欢迎来到概率统计的世界!在量化交易中,概率统计是至关重要的工具。通过理解概率,我们可以用数学的方法来描述市场行为,预测未来走势,并制定交易策略。让我们一起从基础概念开始,逐步深入,揭开概率统计的神秘面纱。 1.1 概率论的基本概念与应用 概率是用来描述某个事件发生可能性的数值。例如,丢一枚硬币,正面朝上的概率是50%。这个概率可以用数学公式表示为: 在量化交易中,我们常常需要计算各种事件的
TensorFlow 2.1.0 + Windows 10 - 64 bit + Python 3.7 安装
先来看看TensorFlow2.1.0安装要求 那就先安装 Python3.7 !!!!!!!!!!!!! 在使用Python时,我们经常需要用到很多第三方库,例如,上面提到的Pillow,以及MySQL驱动程序,Web框架Flask,科学计算Numpy等。用pip一个一个安装费时费力,还需要考虑兼容性。 推荐直接安装 Anaconda,刚好支持Python3.7 下载-安装,一
fftw-2.1.5交叉编译及性能测试记录
1、下载 网络链接很多,这里不提供。 2、编译 tar -xzvf fftw-2.1.5.tar.gz cd fftw-2.1.5 mkdir build_out ./configure --prefix=./build_out --host=arm-linux --enable-float --enable-static --disable-shared CC=aarch64-l
Mac M1Pro 安装Java性能监控工具VisualVM 2.1.9
本地已经安装了java8,在终端输入jvisualvm提示没有安装 zhinian@sara ~ % jvisualvmThe operation couldn’t be completed. Unable to locate a Java Runtime that supports jvisualvm.Please visit http://www.java.com for info
Datawhale X 李宏毅苹果书 AI夏令营(深度学习进阶)taks2(2.1+2.2+2.3)
task2.1 自适应学习率 临界点其实不一定是在训练一个网络的时候会遇到的最大的障碍。 一般在训练一个网络的时候,损失原来很大,随着参数不断的更新,损失会越来越小,最后就卡住了,损失不再下降。当我们走到临界点的时候,意味着梯度非常小,但损失不再下降的时候,梯度并没有真的变得很小。看下图就可以看出来 范数(norm),即梯度这个向量的长度 随着迭代次数增多,虽然损失不再下降,但是梯度
phantomjs-2.1.1-windows
需要用一下PhantomJS https://phantomjs.org/download.html 直奔官网而去 不过这也太慢了吧 我是shoufa好公民 没有可以出去的软件 下载了很久很久。。。 由于太恶心度盘,我上传了个蓝盘,就不传csdn下载了 有需要的下吧,这速度嗖嗖的 下载:https://www.lanzous.com/ia60sfe 密码:be0e 找到了
【C++ Primer Plus习题】2.1
问题: 解答: #include <iostream>using namespace std;int main(){cout << "在下国林!" << endl;cout << "家住天府之国!" << endl;return 0;} 运行结果: 考查点: 预处理头文件命名空间main函数c++的标准输出和换行字符串常量 开个新坑,O(∩_∩)O哈哈~ 2024年8
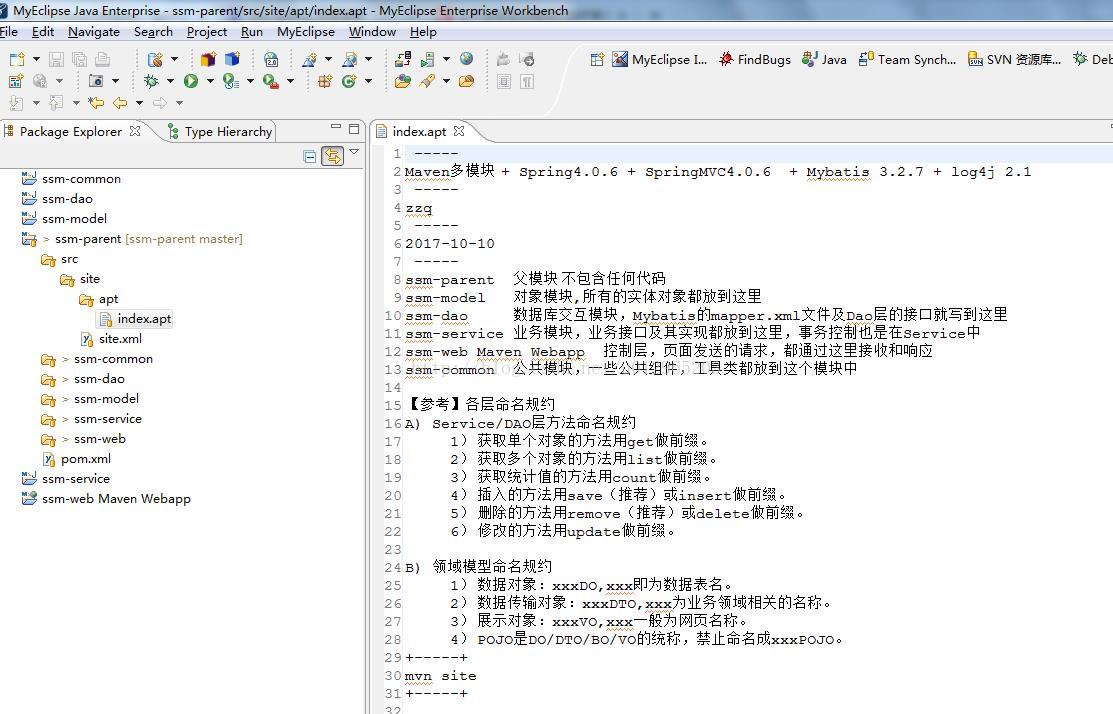
Maven多模块 + Spring4.0.6 + SpringMVC4.0.6 + Mybatis 3.2.7 + log4j 2.1
参考: http://www.cnblogs.com/gwx238044/articles/6633252.html githud : https://github.com/2014team/Maven--Spring4.0.6-SpringMVC4.0.6-Mybatis-3.2.7-log4j-2.1
2.1 满足条件的整数
1943:满足条件的整数 描述 假设a、b、c均为整数,且满足a,b,c 大于1,并且小于等于100,找出所有符合条件:“a2+ b2= c2”的整数组。 输入 无。 输出 按a从小到大的顺序输出所有满足条件的整数组(若a相同,则按b从小到大的顺序输出),每行一组,每一组数据的输出样式为: a + b = c*c 注意: 1)为避免重复输出,要求a<=b;2)加号和等号左右各有一个
Django 2.1.7 状态保持 - Cookie
在之前写jquery的篇章中介绍过Cookie的一个示例用法jquery cookie示例 - 只提示一次的弹框. 这是使用jquery的插件使用的功能,本篇章来介绍使用Django的示例用法。 下面先来看一些概念描述。 状态保持 浏览器请求服务器是无状态的。无状态指一次用户请求时,浏览器、服务器无法知道之前这个用户做过什么,每次请求都是一次新的请求。无状态的应用层面的
Django 2.1.7 视图 - HttpResponse对象、子类JsonResponse、子类HttpResponseRedirect
关于视图的篇章 Django 2.1.7 视图Django 2.1.7 MVT模型示例 - 查询数据,返回渲染模板数据Django 2.1.7 视图 - 自定义404错误、500错误Django 2.1.7 视图 - HttpReqeust对象、QueryDict对象 HttpResponse对象 视图在接收请求并处理后,必须返回HttpResponse对象或子对象。在
Django 2.1.7 视图 - HttpReqeust对象、QueryDict对象
关于视图的篇章 Django 2.1.7 视图Django 2.1.7 MVT模型示例 - 查询数据,返回渲染模板数据Django 2.1.7 视图 - 自定义404错误、500错误 在前面的篇章基本讲述了视图的使用,那么本篇章主要是来看看Django中的HttpReqeust对象。 HttpReqeust对象 服务器接收到http协议的请求后,会根据报文创建Http
Django 2.1.7 视图 - 自定义404错误、500错误
上一篇Django 2.1.7 模型管理器 models.Manager 以及 元选项 讲述了关于Django模型管理类以及如何设置表名、字段名的元选项内容。 在了解了Django的模型相关知识点之后,那么再来详细看看Django的视图。 前面我也基本写了Django 2.1.7 视图,讲解了url地址的转发配置,参数获取等内容。 那么本篇章再看看如何自定义404错误、
Django 2.1.7 模型管理器 models.Manager 以及 元选项
上一篇Django 2.1.7 模型的关联 讲述了关于Django模型一对多、多对多、自关联等模型关系。 在查询数据的时候,对于某种固定的查询,例如视图之类的查询,通用类型的查询每次都需要写一遍,有没有一个地方可以将这类通用的查询抽象出来,进行模型的业务管理呢? 这时候就要看看模型的管理器了。 参考文献 https://docs.djangoproject.com/z
Django 2.1.7 查询集 QuerySet
上一篇Django 2.1.7 模型 - 条件查询 F对象 Q对象 聚合查询讲述了关于Django模型的介绍F对象、Q对象、聚合查询等功能。 不管什么查询,返回的结果都基本是查询集QuerySet,如下: In [16]: MiddlewareInfo.objects.all()Out[16]: <QuerySet [<MiddlewareInfo: Middlewar
Django 2.1.7 模型 - 条件查询、模糊查询、空查询、比较查询、范围查询、日期查询...
上一篇Django 2.1.7 模型 - MVT模型增删功能讲述了关于MVT模型中列表的增加数据以及删除数据的功能,在数据返回的过程中,也有部分关于模型之间关联查询的数据。 本篇章将着重讲述模型之间的关联查询。 参考文献 https://docs.djangoproject.com/zh-hans/2.1/topics/db/queries/ 打开mysql数据中的日